Day 10 : Brownian Excursion

Day 10 : Brownian Excursion#

A Brownian excursion is yet another stochastic process which arises from a Weiner process (standard Brownian motion) with the additional condition that it stays positive over a given interval and ends at zero. It is particularly significant in probability theory, combinatorics, and applications like queuing theory and random geometry.

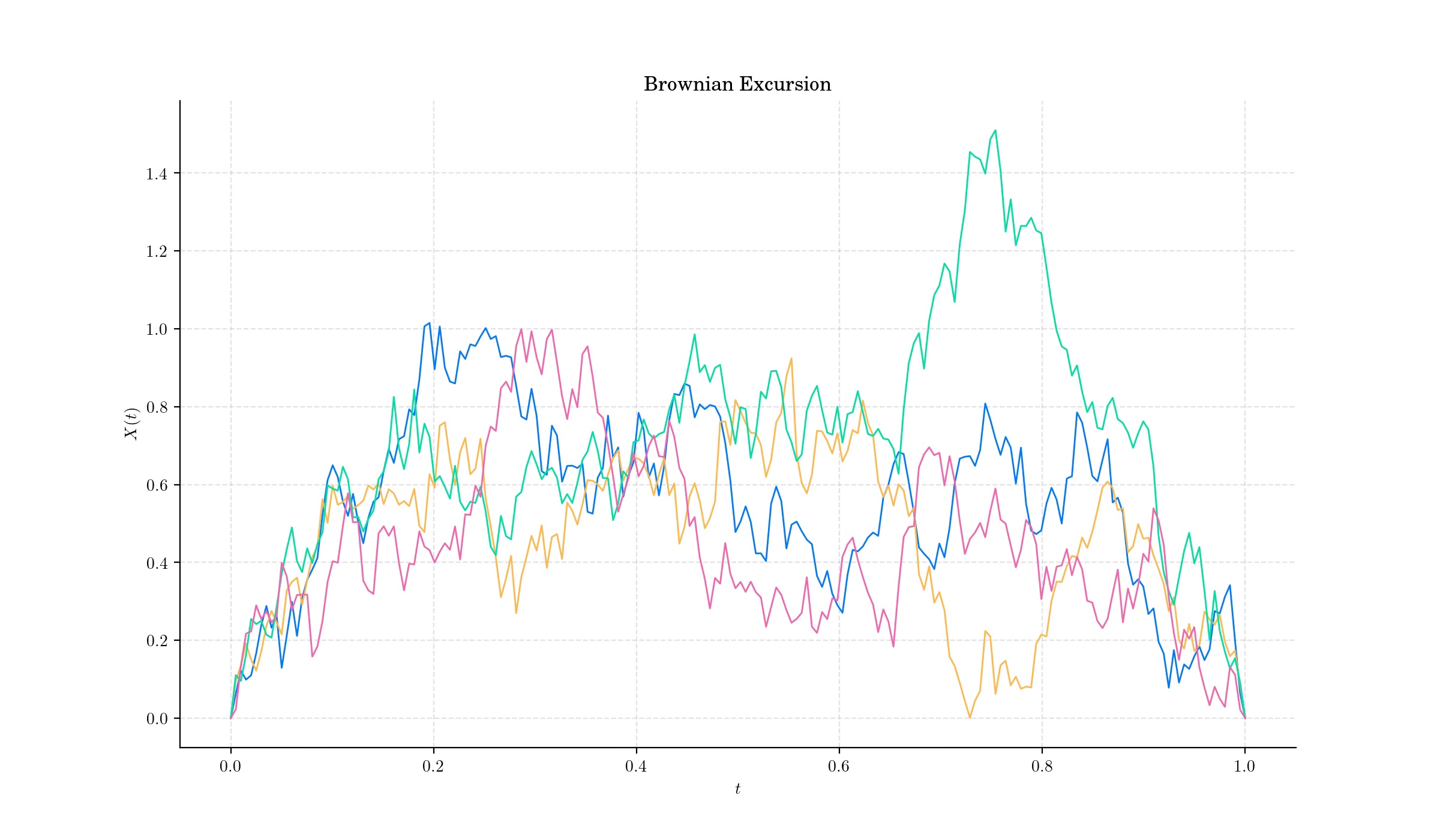
Definition#

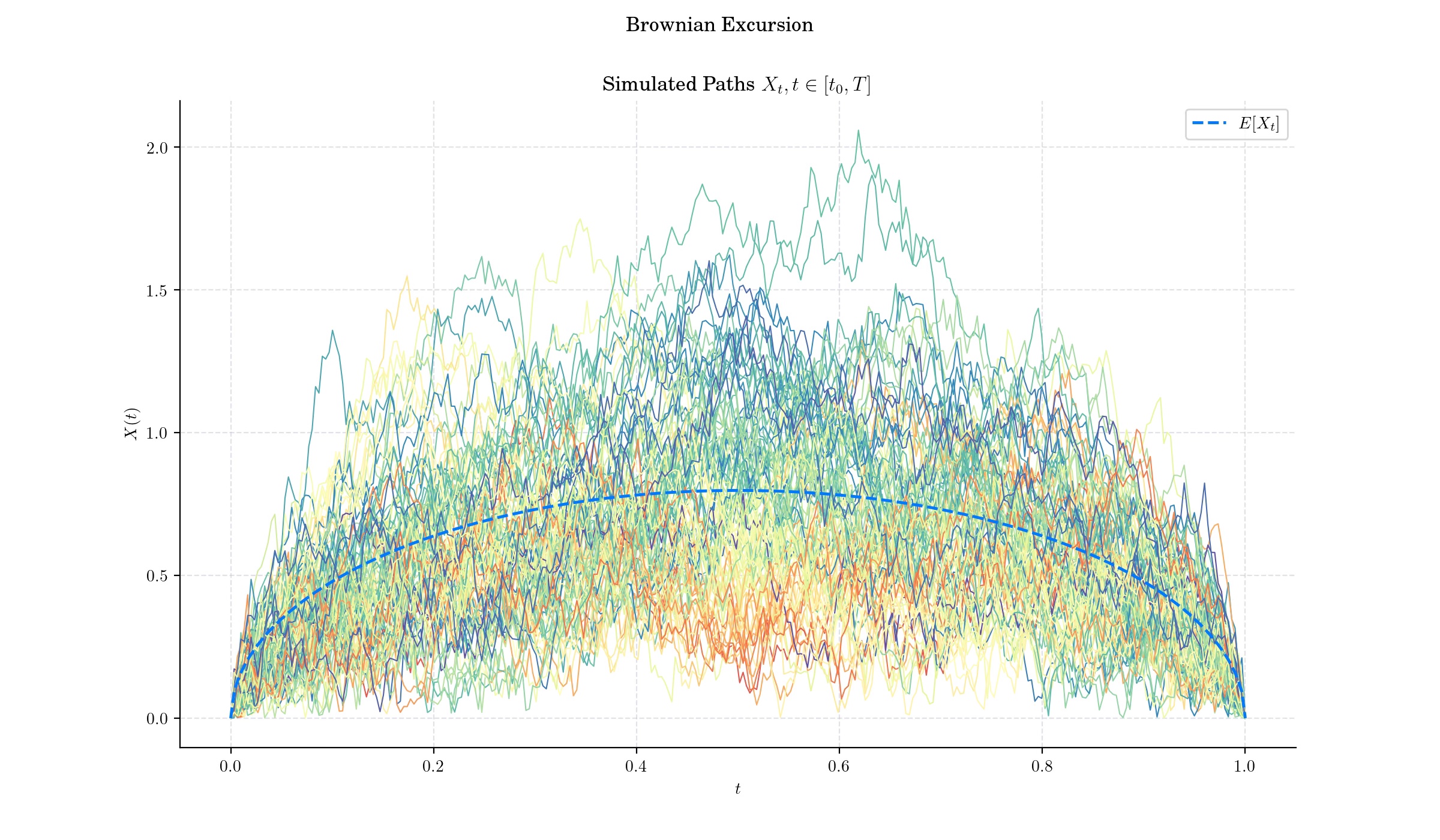
A normalised Brownian excursion is a nonnegative real-valued stochastic process \(X\) defined on the interval \(\[0,1\]\) which can be constructed from a standard Brownian motion \(W\) on \(\[0,T\]\) by conditioning on it being nonnegative on \((0,T)\) and equal to zero at the end time. Alternatively, it is a Brownian bridge process conditioned to be positive.

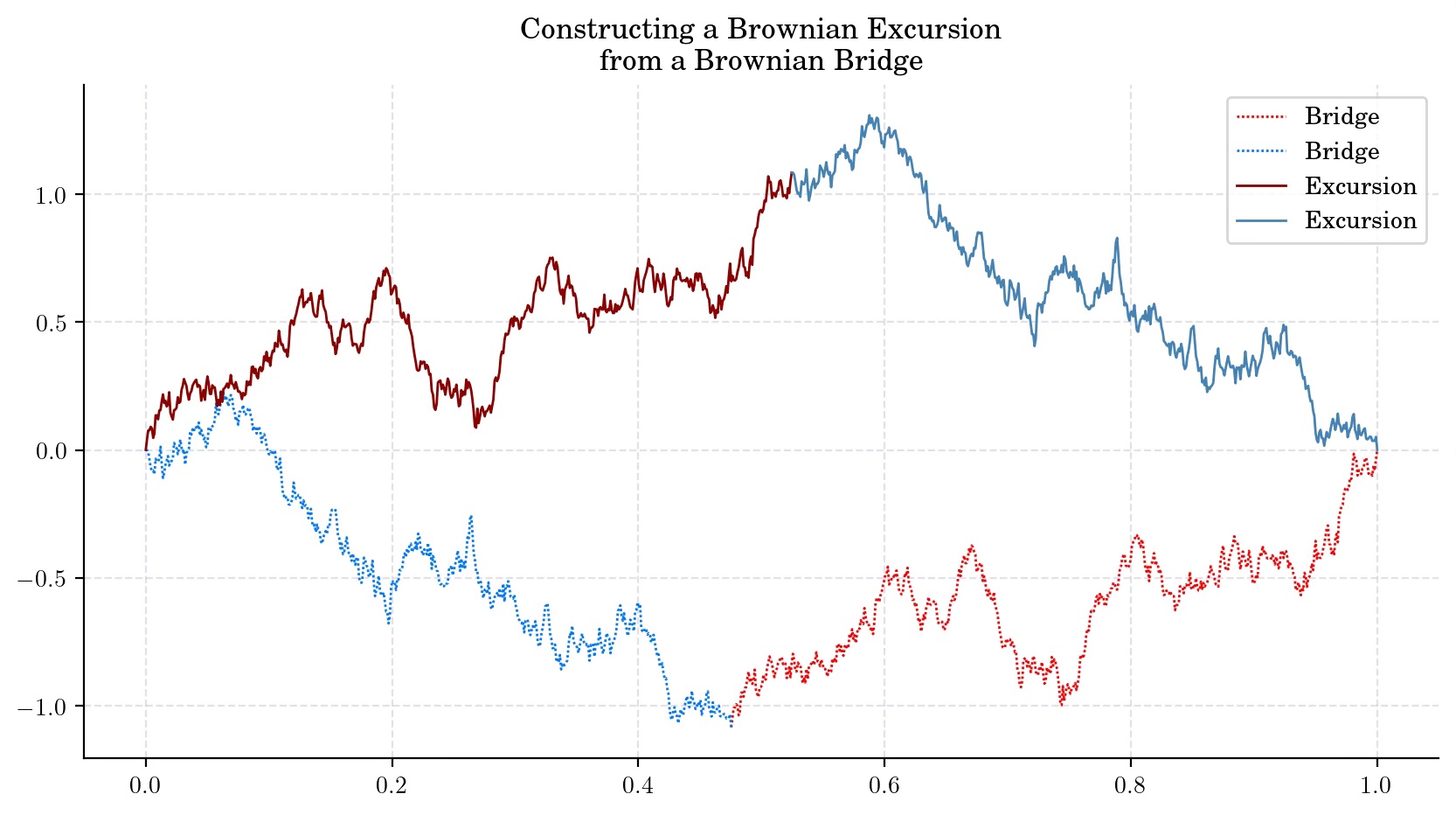
We can obtain a Brownian Excursion from a Brownian Bridge path by using the so called Vervaat construction. Let \(\tau\_m\) be the time at which a Brownian Bridge process \(W\_b\) achieves its minimum on \(\[0, 1\]\). Vervaat (1979) shows that the process defined as:

\[\{W\_b(\tau\_m + t \mod 1) - W\_b(\tau\_m), \quad 0\leq t\leq 1 \},\]

is a Brownian excursion.

đź”” Random Facts đź””#

  • Brownian Excursions are deeply connected to combinatorial structures, particularly random trees and Catalan numbers. See https://cs.uwaterloo.ca/journals/JIS/VOL14/Whitt/whitt6.pdf

  • In polymer physics, the shape of a polymer chain confined to a half-plane (or subject to some spatial constraint) can be modeled by a Brownian Excursion.

  • If \(X(t)\) is a Brownian excursion then so is \(\tilde{X}(t) = X(1-t)\).

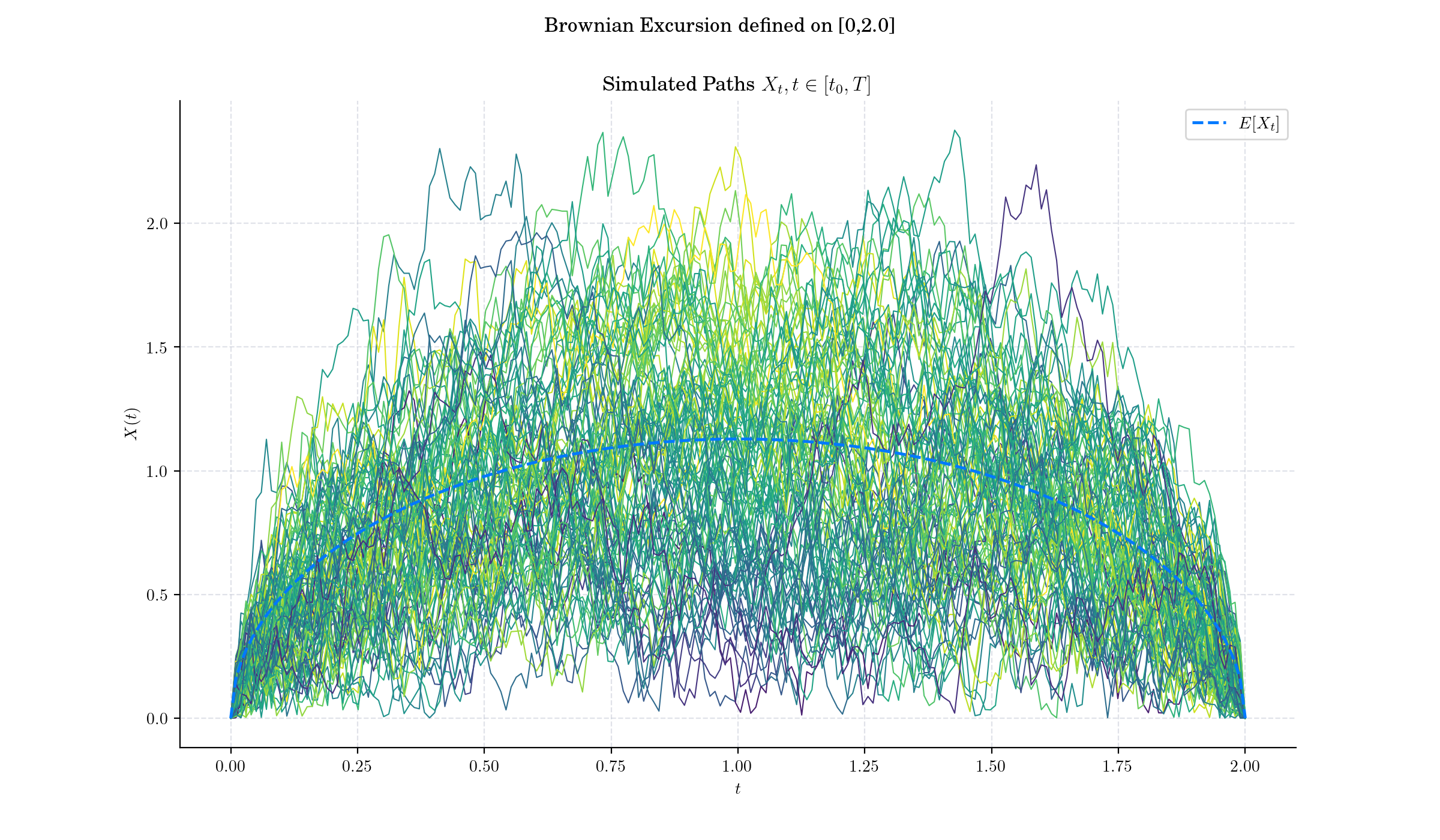
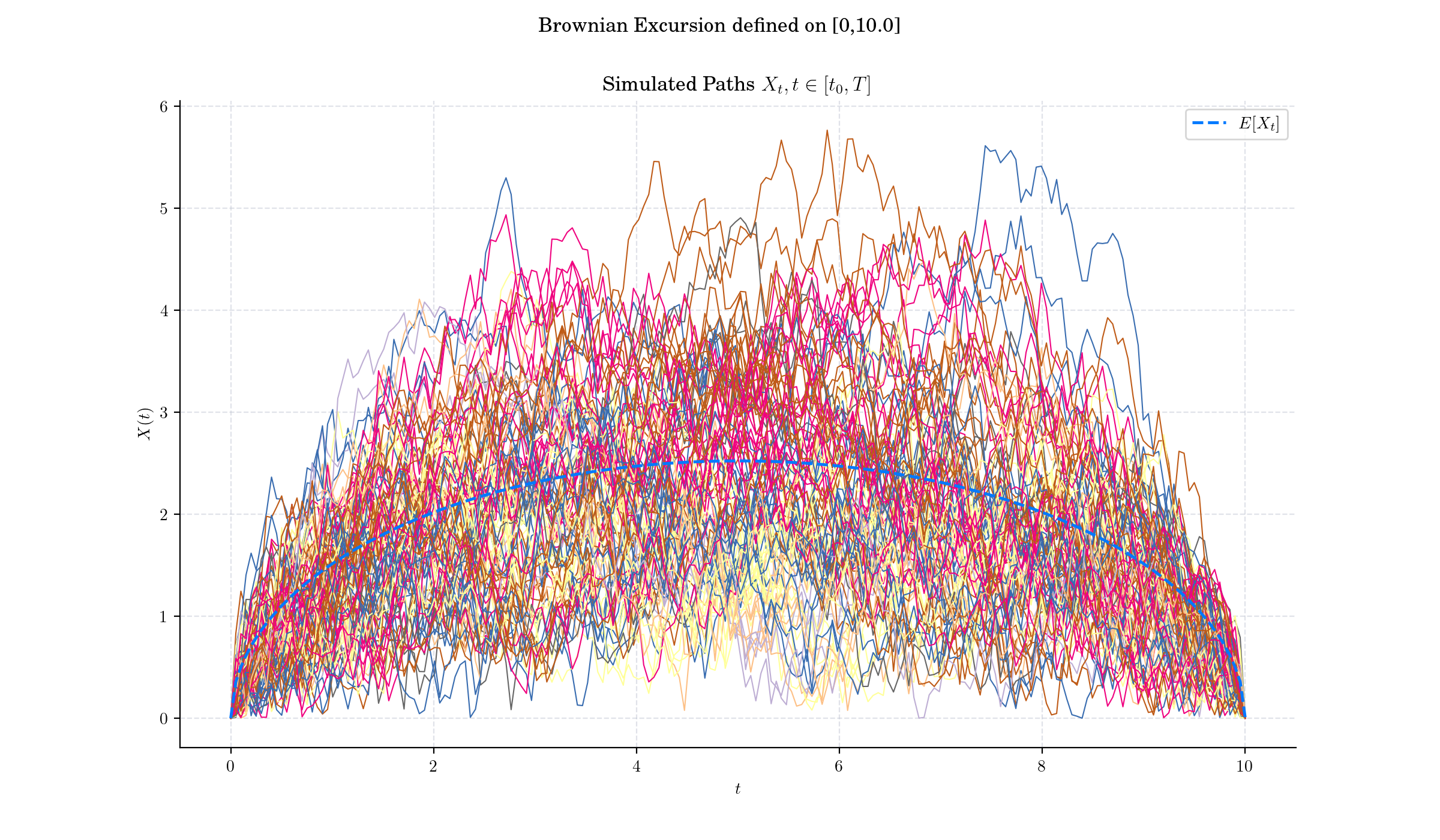
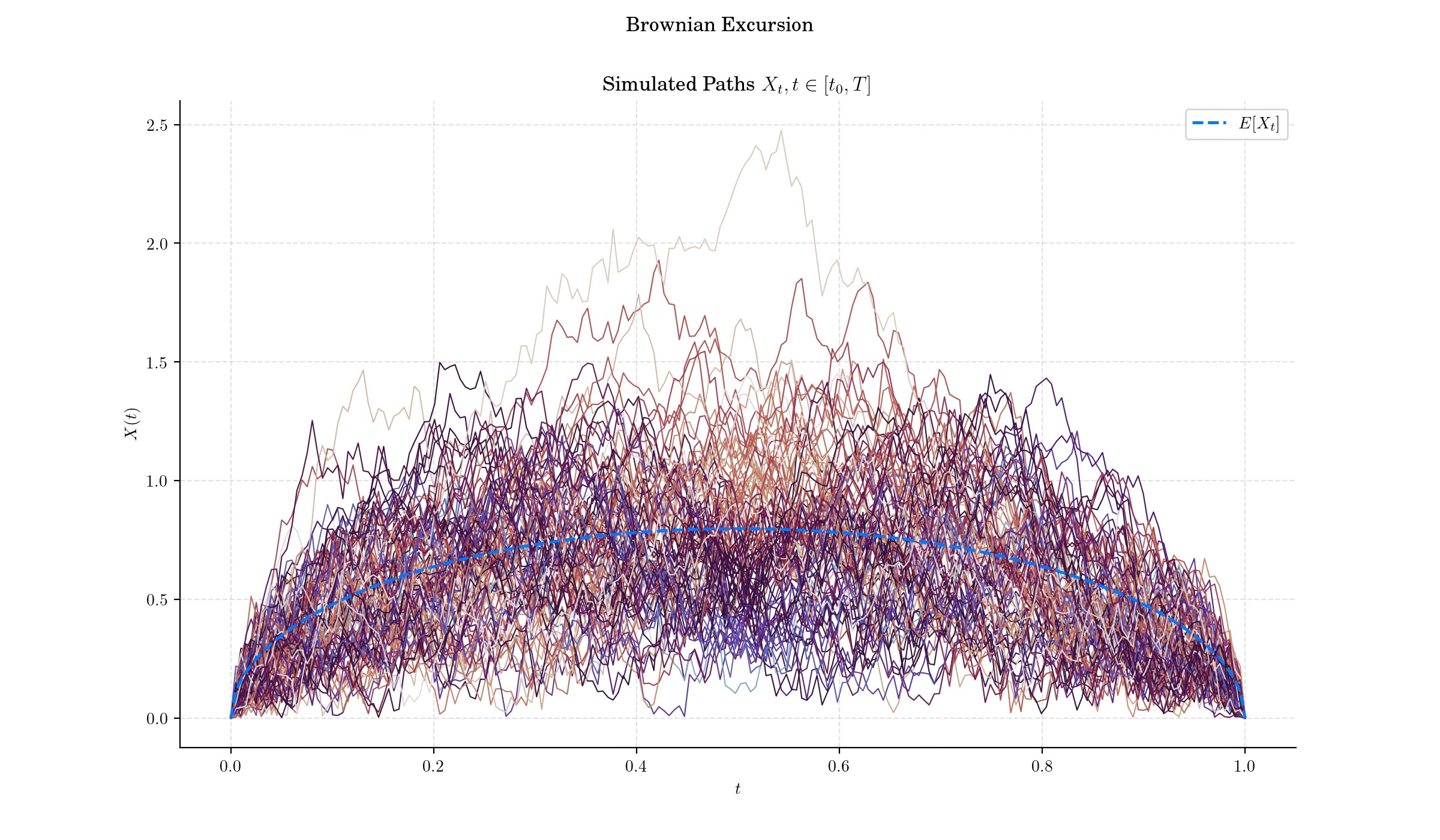
More to Read đź“š#

  • Jim Pitman. “Brownian Motion, Bridge, Excursion, and Meander Characterized by Sampling at Independent Uniform Times.” Electron. J. Probab. 4 1 - 33, 1999. https://doi.org/10.1214/EJP.v4-48

  • Knight, Frank B. “On the Excursion Process of Brownian Motion.” Transactions of the American Mathematical Society, vol. 258, no. 1, 1980, pp. 77–86. JSTOR, https://doi.org/10.2307/1998281. Accessed 10 Dec. 2024.

  • Kai Lai Chung. “Maxima in Brownian excursions.” Bull. Amer. Math. Soc. 81 (4) 742 - 745, July 1975.

P.s. If you are curious about probability distributions visit the Advent Calendar 2023 ✨

Contents