Day 11 : Brownian Meander#

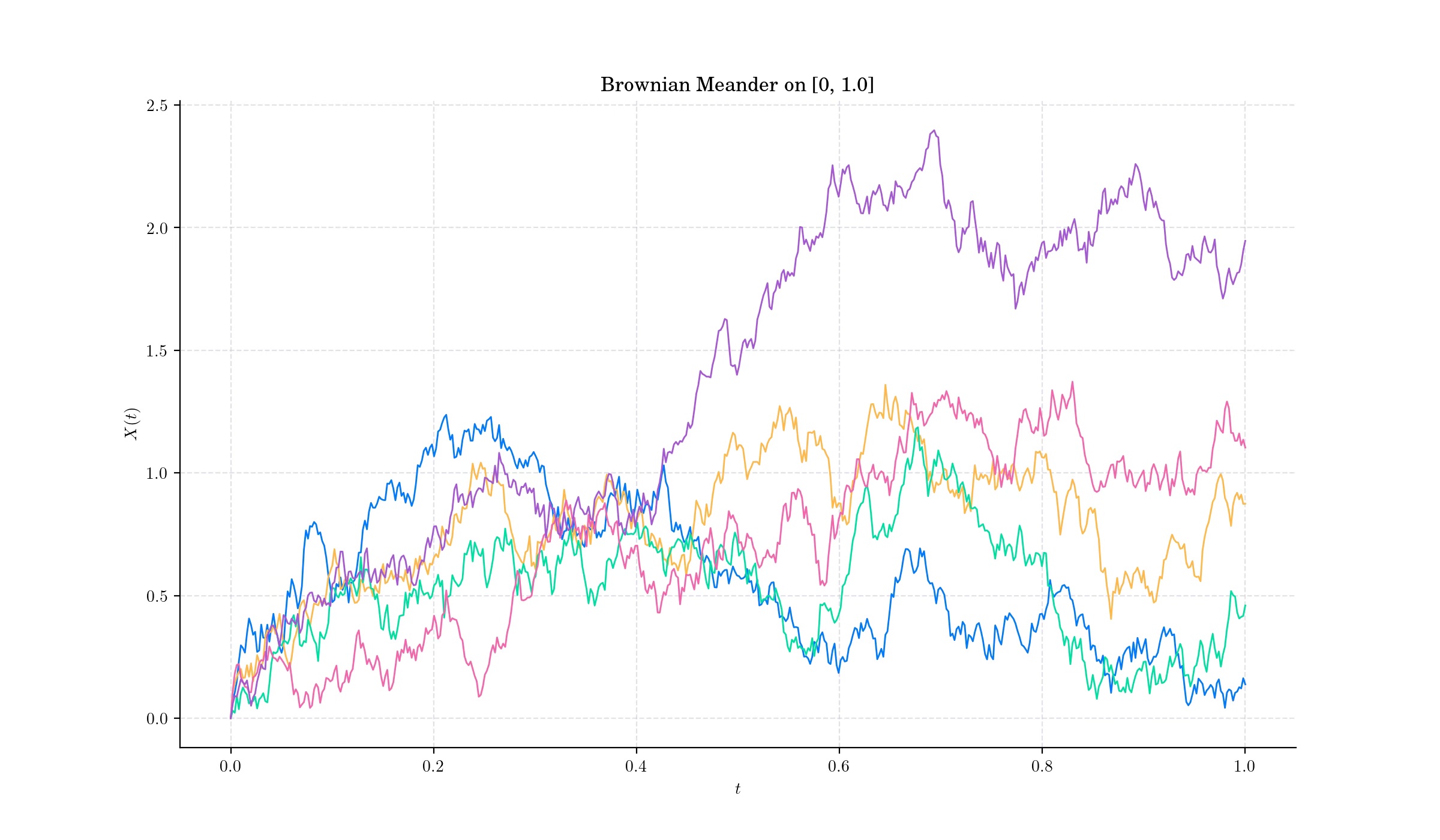
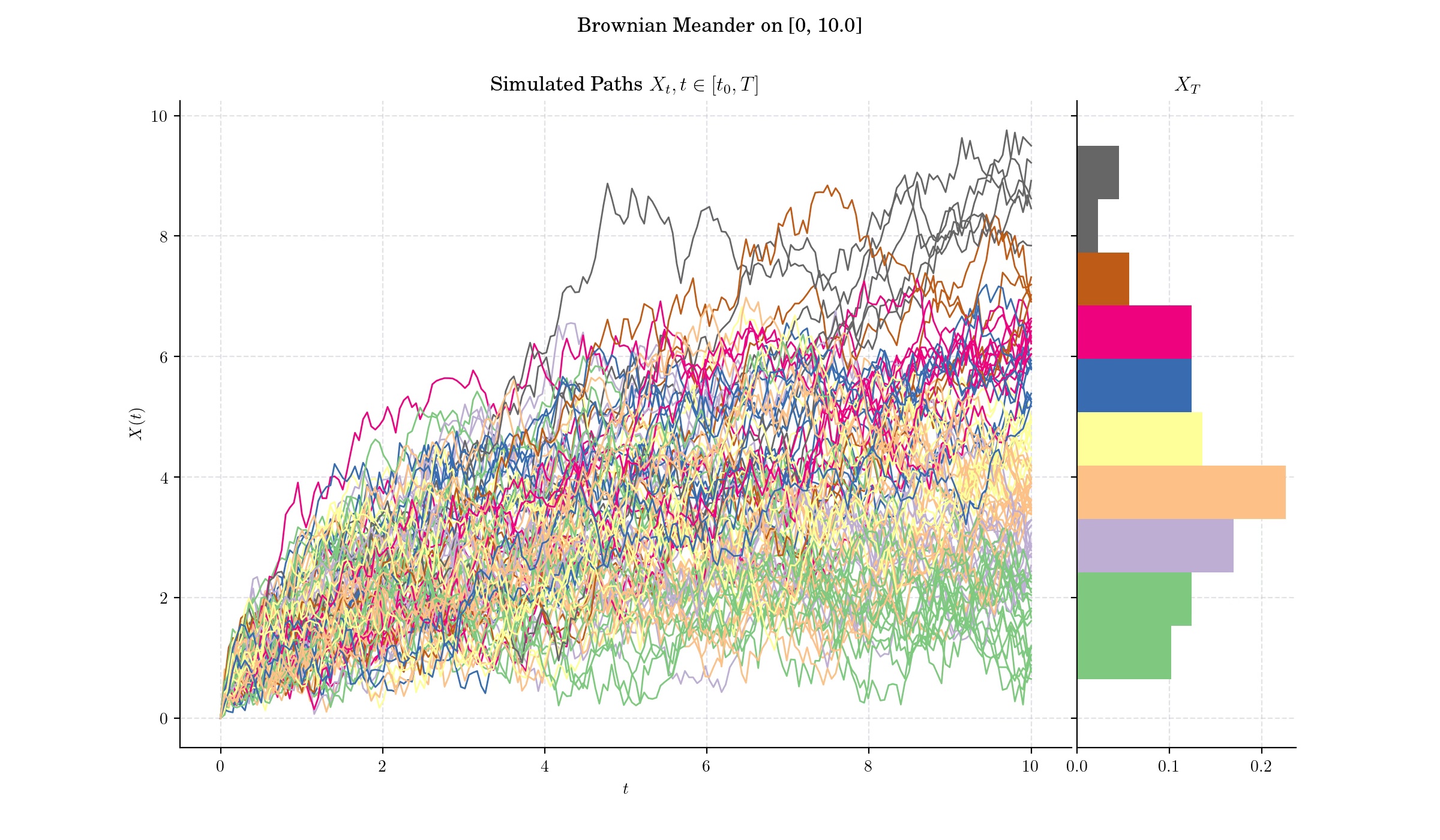
A Brownian Meander is yet another stochastic process which arises from a Weiner process (standard Brownian motion) with the additional condition that it stays positive over a given interval.

Definition#

Let $W=\{W(t), t\geq 0\}$ be a standard one-dimensional Brownian motion, and

\[\tau = \sup\{ t\in \[0,1\] : W(t) = 0 \},\]

i.e. the last time before $t=1$ when W visits zero. Then the Brownian meander is defined by the following expression

\[X(t) = \frac{1}{1 - \tau} | W(\tau + t(1-\tau)) |, \qquad t \in \[0,1\].\]

That is, given the last time before 1 that a standard Brownian motion visits zero (note that $\tau <1$ almost surely), we snip off and discard the trajectory before $\tau$, and scale the remaining part so that it spans a time interval of length 1. The scaling factor for the spatial axis must be square root of the scaling factor for the time axis. The process resulting from this snip-and-scale procedure is a Brownian meander.

🔔 Random Facts 🔔#

Both the Brownian Meander and the Brownian Excursion arise as the limit process in the study of the behaviour of random walks conditioned to stay positive.
Brownian meanders emerge in path decompositions of the Brownian motion. In particular Denisov (1984) showed that a Brownian motion around a maximum point can be represented (in law) by means of a two-sided Brownian meander, which is constructed by gluing together two meanders.
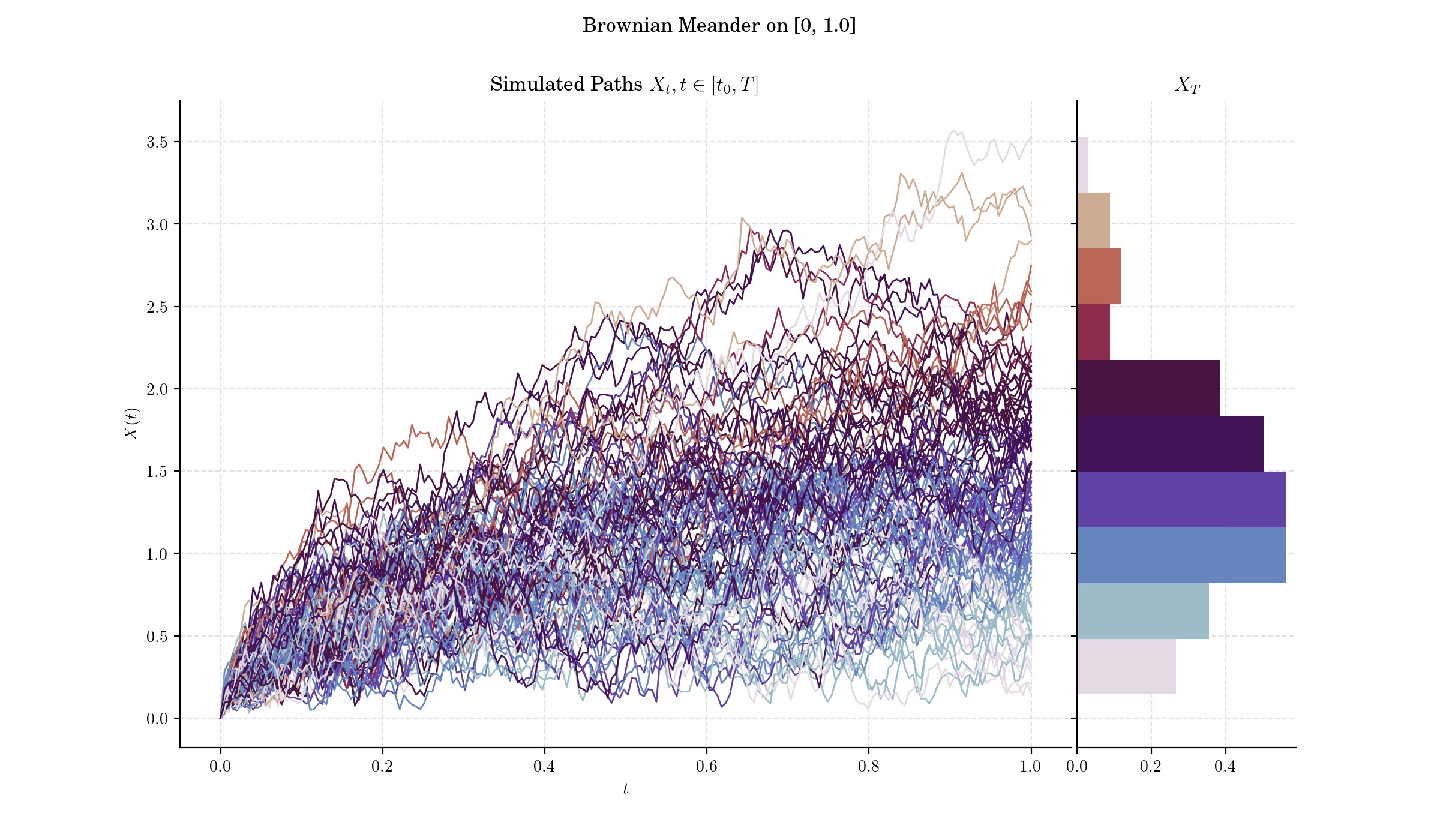
If $X$ is a Brownian meander then $X(t)$ has probability density $$ 2 t^{-\frac{3}{2}} x e^{-\frac{x^2}{2t}} \Phi\_{1-t}(x), \qquad x>0, t \in \[0,1\].$$
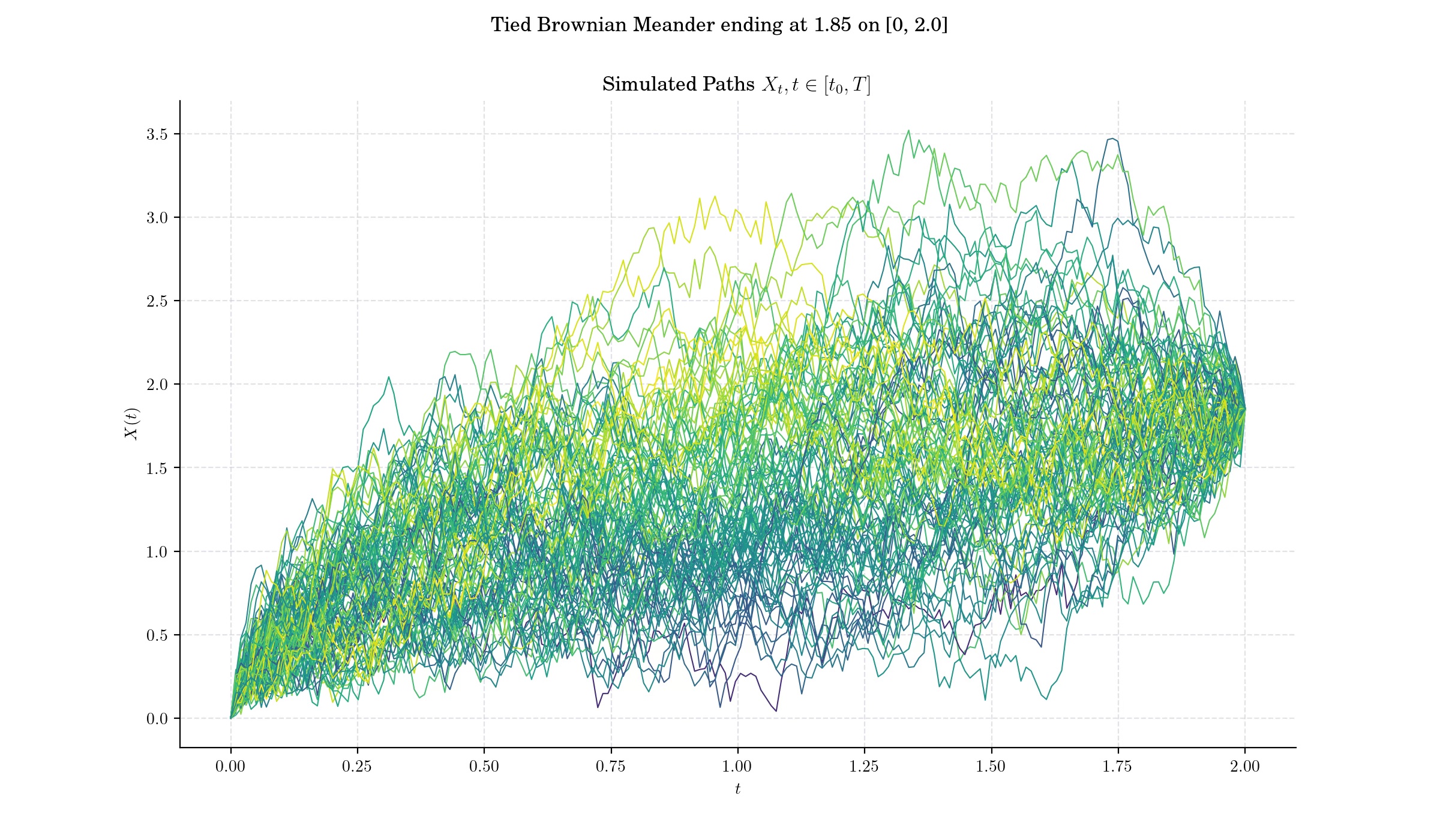
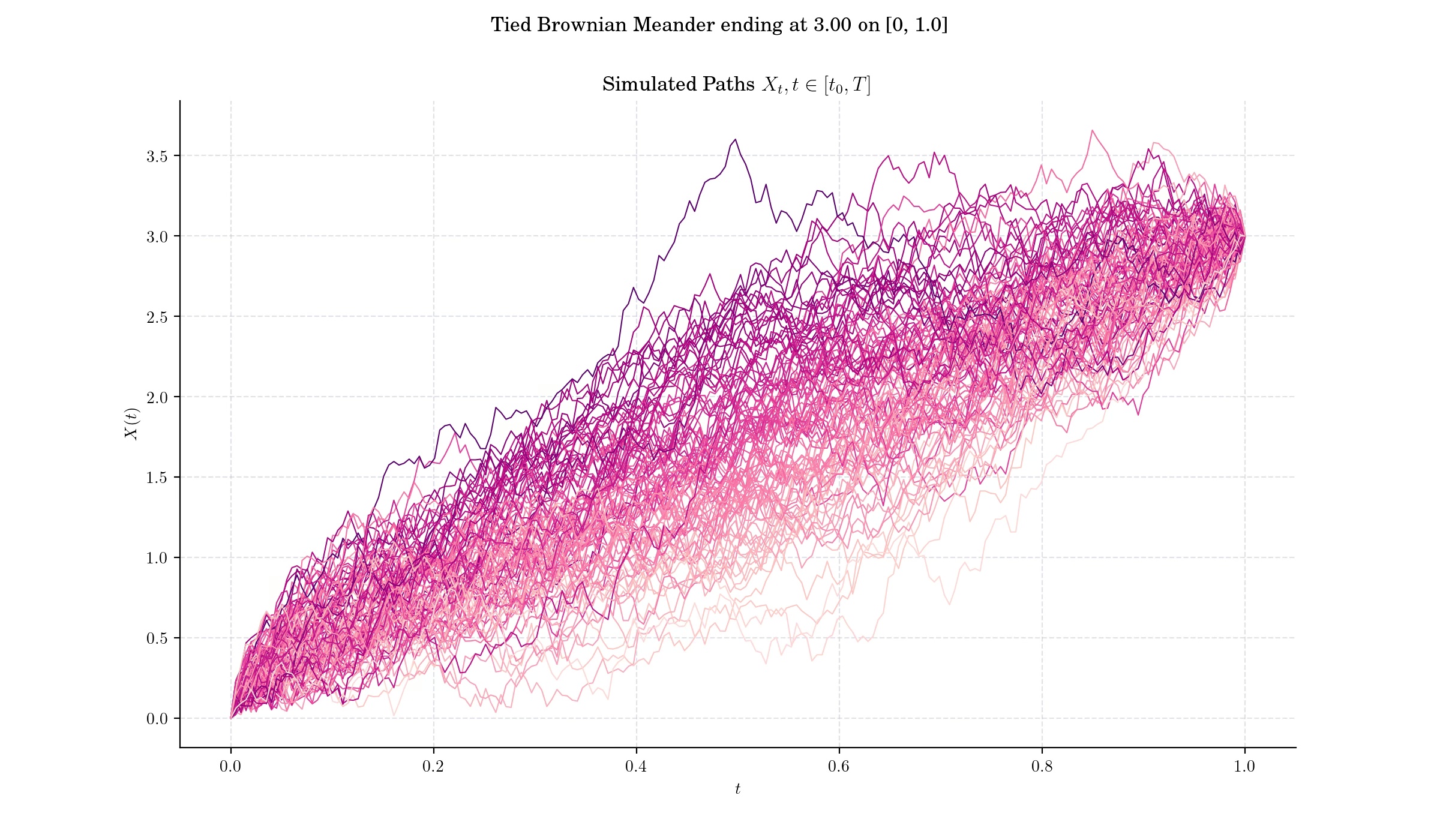
In a similar fashion as the Brownian Bridge, the Brownian Meander can be restricted to end on a particular point. Such process is the so-called a Tied Brownian Meander. The Tied Brownian Meander has more complicated distributional properties compared to the unconstrained Brownian motion or the regular meander.

Day 11 : Brownian Meander

Contents

Day 11 : Brownian Meander#

Definition#

🔔 Random Facts 🔔#

More to Read 📚#