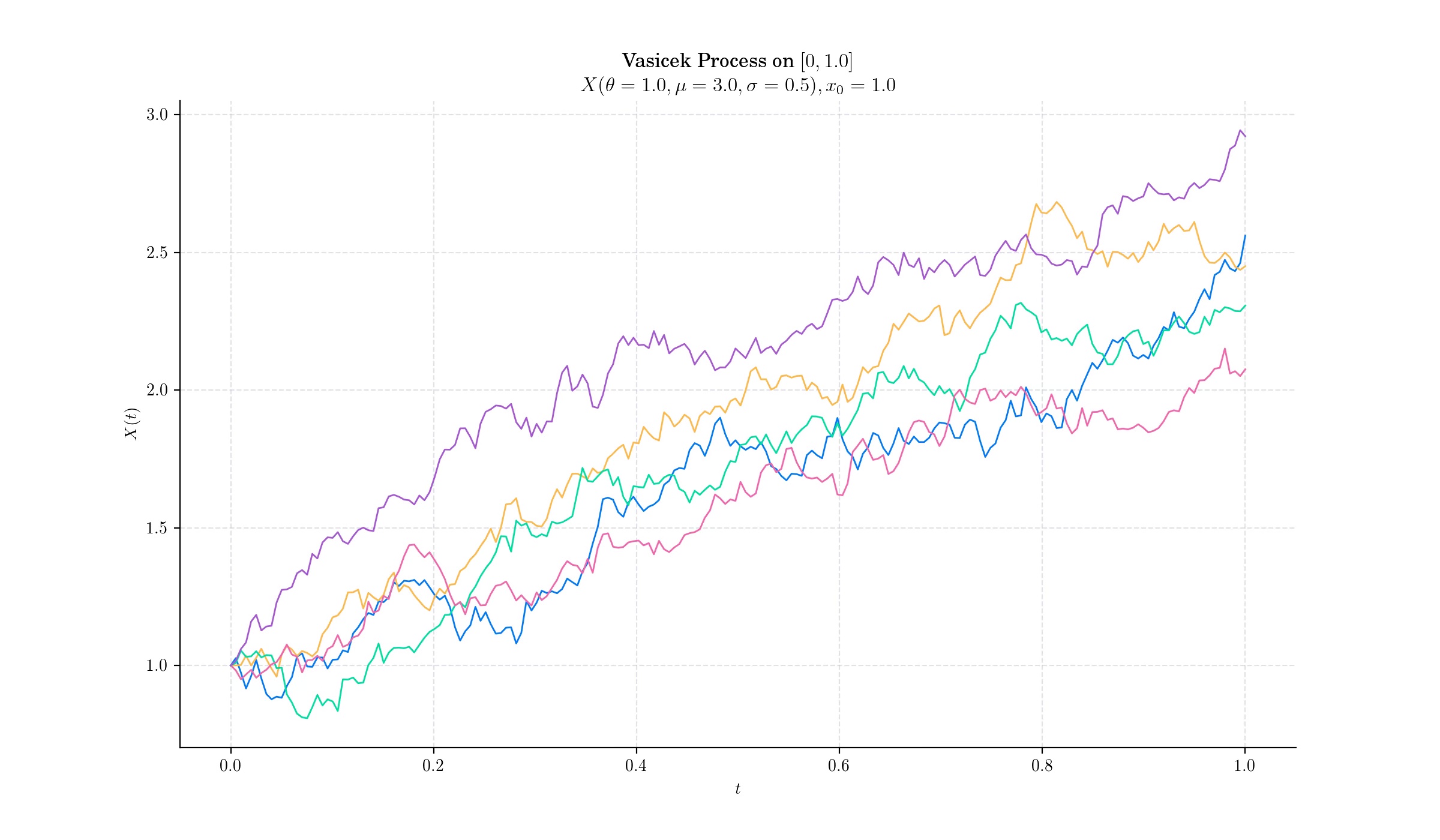
Day 13 : Vasicek Model (Ornstein-Uhlenbeck continuation)#

The Vasicek Model is one of the earliest and most influential mathematical frameworks for modeling interest rates. Developed by Czech mathematician Oldřich Vašíček in 1977, the model is a cornerstone of financial mathematics, especially in the valuation of bonds and interest rate derivatives.

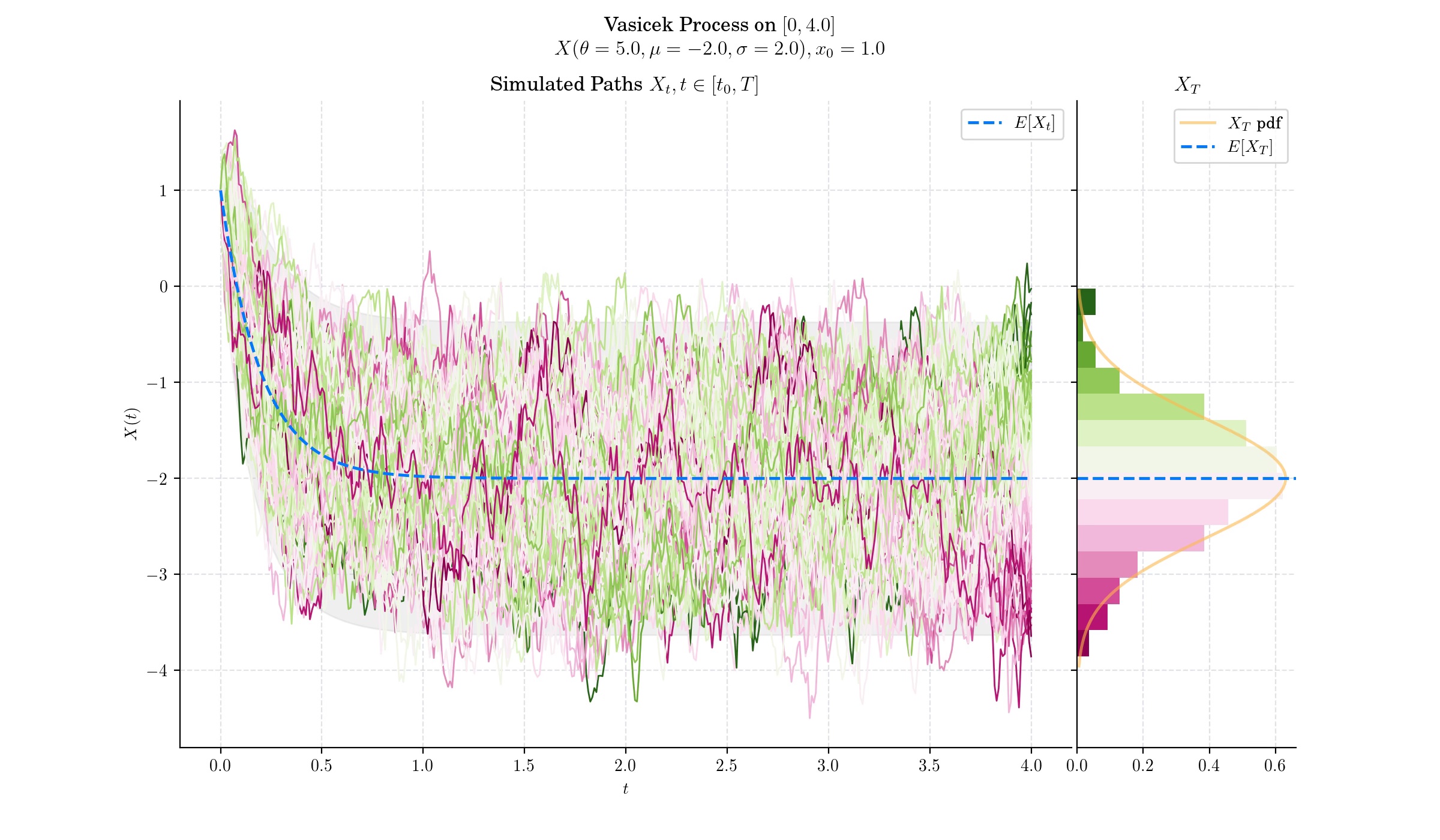
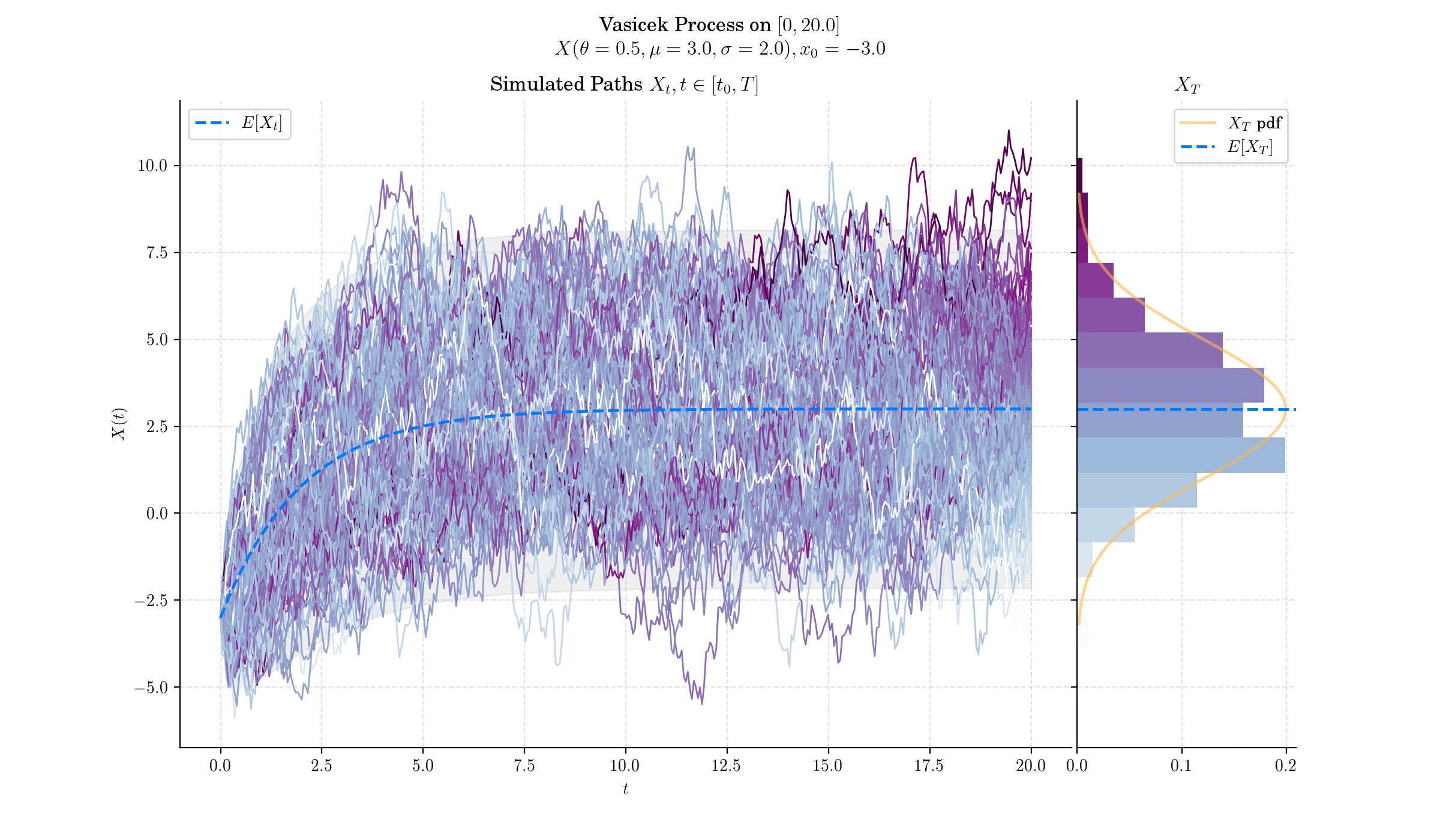
The Vasicek Model is a one-factor short-rate model as it describes interest rate movements as driven by only one source of market risk whose dynamics follow an Ornstein-Uhlenbeck process, known for its mean-reverting properties, which ensure that interest rates do not drift infinitely upward or downward.

Definition#

Under the Vasicek model, the dynamics of the instantaneous interest rate are defined by the following the stochastic differential equation:

\[dX\_t = \theta(\mu - X\_t) dt + \sigma dW\_t, \qquad \geq 0,\]

with initial condition \(X\_0 =x\_0\in\mathbb{R}\), and where \(W\) is a standard Brownian motion, and the three parameters are constants:

- \(\theta>0\) : speed or mean reversion coefficient

- \(\mu \in \mathbb{R}\) : long term mean

- \(\sigma>0\) : volatility

In order to find the solution to this SDE, let us set the function \(f(t,x) = x e^{\theta t}\). Then, Ito’s formula implies

\[X\_te^{\theta t} = x\_0 +\int\_0^t X\_s \theta e^{\theta s}ds + \int\_0^t e^{\theta s}dX\_s\]

\[ = x\_0 + \int\_0^t \left\[ \theta X\_s e^{\theta s} +\theta e^{\theta s}(\mu - X\_s)\right\] ds + \int\_0^t e^{\theta s}\sigma dW\_s\]

\[ = x\_0 + \int\_0^t \left\[ \theta e^{\theta s}\mu\right\] ds + \int\_0^t e^{\theta s}\sigma dW\_s\]

\[ = x\_0 + \mu(e^{\theta t} - 1) + \int\_0^t e^{\theta s}\sigma dW\_s.\]

Thus

\[X\_t = x\_0e^{-\theta t} + \mu(1- e^{-\theta t}) + \sigma \int\_0^t e^{-\theta (t-s)}dW\_s., \]

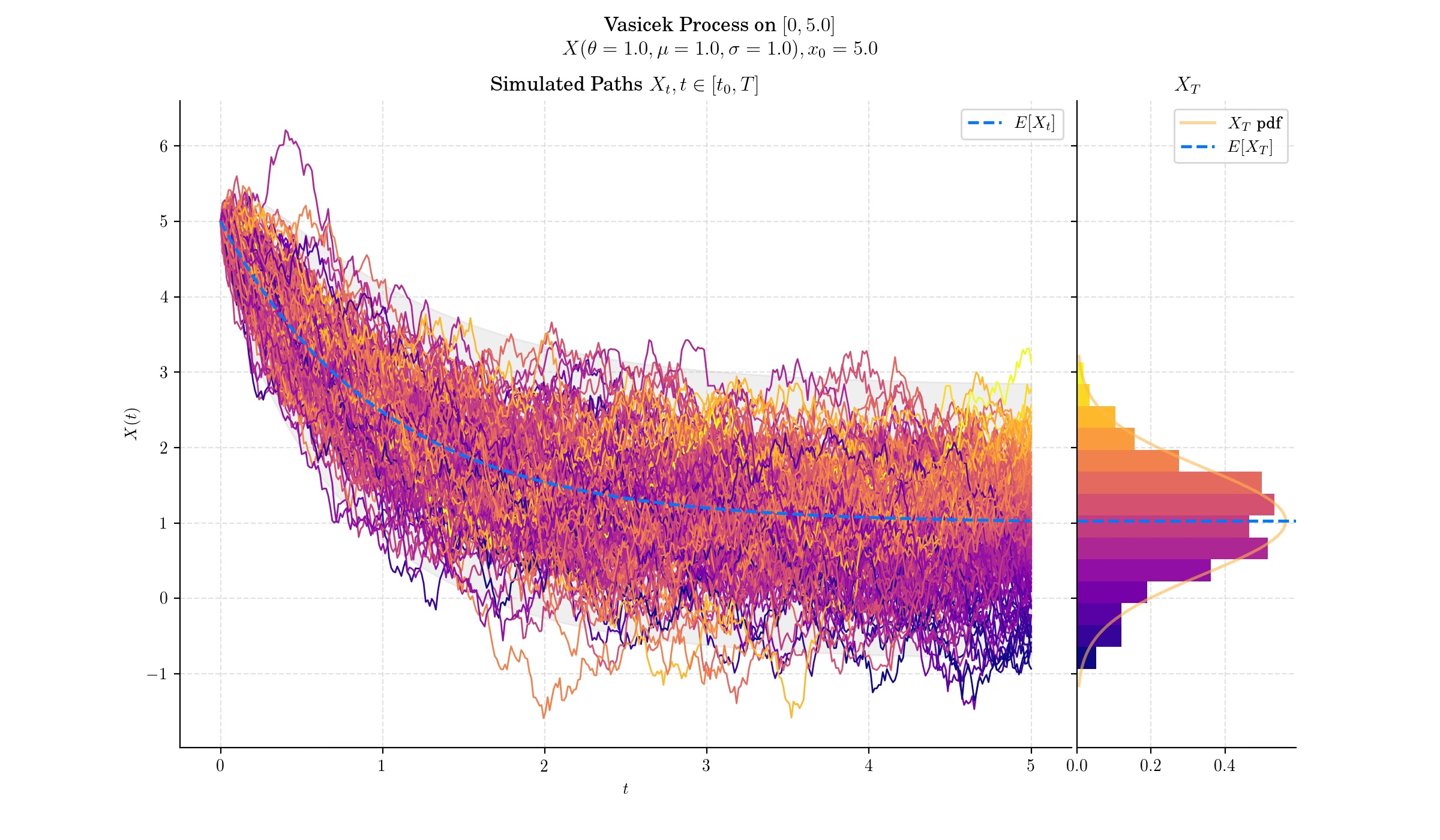
This expression implies that for each \(t>0\), the random variable \(X\_t\) follows a normal distribution –since it can be expressed as the sum of a deterministic part and the integral of a deterministic function with respect to the Brownian motion.

🔔 Random Facts 🔔#

Vasicek introduced the model in his 1977 paper “An Equilibrium Characterization of the Term Structure” published in the Journal of Financial Economics. His work was motivated by the need for a rigorous framework to explain the dynamics of interest rates and the term structure of bond yields.
Interest rates in the Vasicek Model naturally drift back to the long-term mean \(\mu\) over time, at a speed governed by the parameter \(\theta\). This aligns with economic observations where extreme interest rate levels are unsustainable and mean reversion is observed.
The Vasicek Model is an affine model, meaning bond prices and yields can be expressed as exponential-affine functions of time and the short rate. This property facilitates analytical pricing of zero-coupon bonds.
The model has closed-form solutions for bond prices, making it computationally efficient and widely adopted in practice.

Day 13 : Vasicek Model (Ornstein-Uhlenbeck continuation)

Contents

Day 13 : Vasicek Model (Ornstein-Uhlenbeck continuation)#

Definition#

🔔 Random Facts 🔔#

More to Read 📚#