Day 12 : Ornstein-Uhlenbeck

Day 12 : Ornstein-Uhlenbeck#

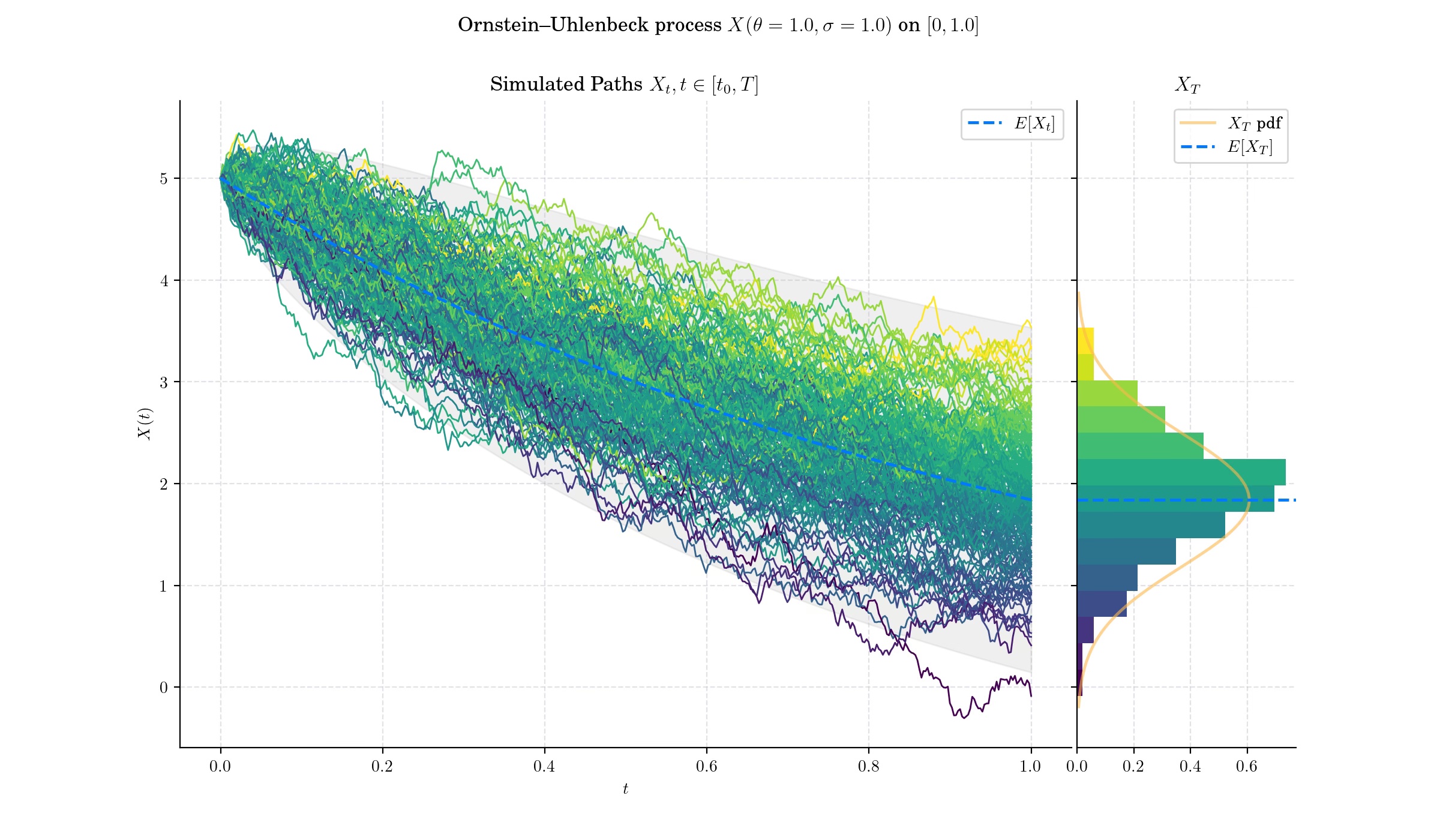
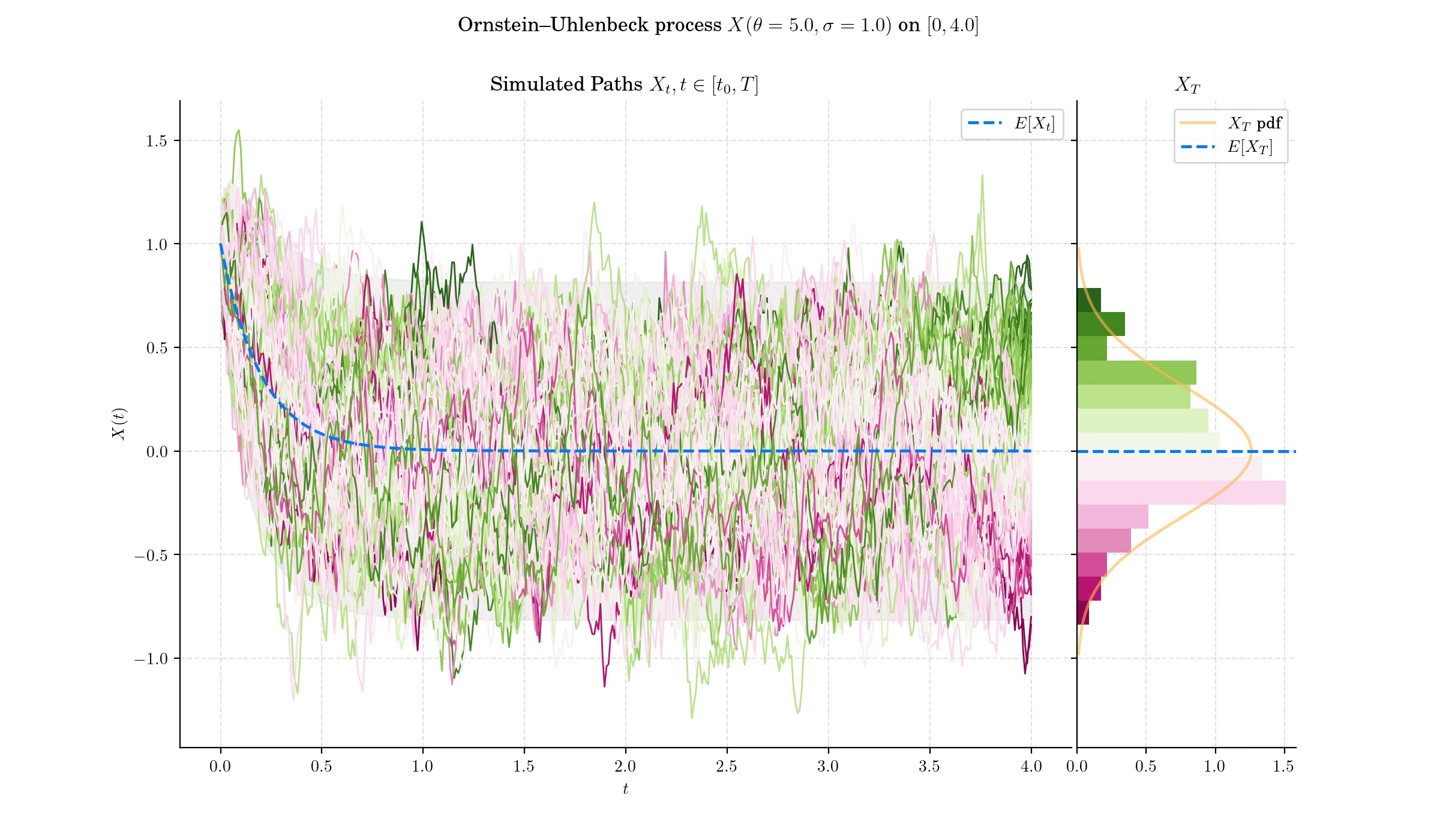
The Ornstein-Uhlenbeck (OU) process is a stochastic process that plays a critical role in fields like physics, finance, and biology. It is a type of Gaussian process known for its mean-reverting properties, making it particularly useful for modelling phenomena that oscillate around a long-term average.

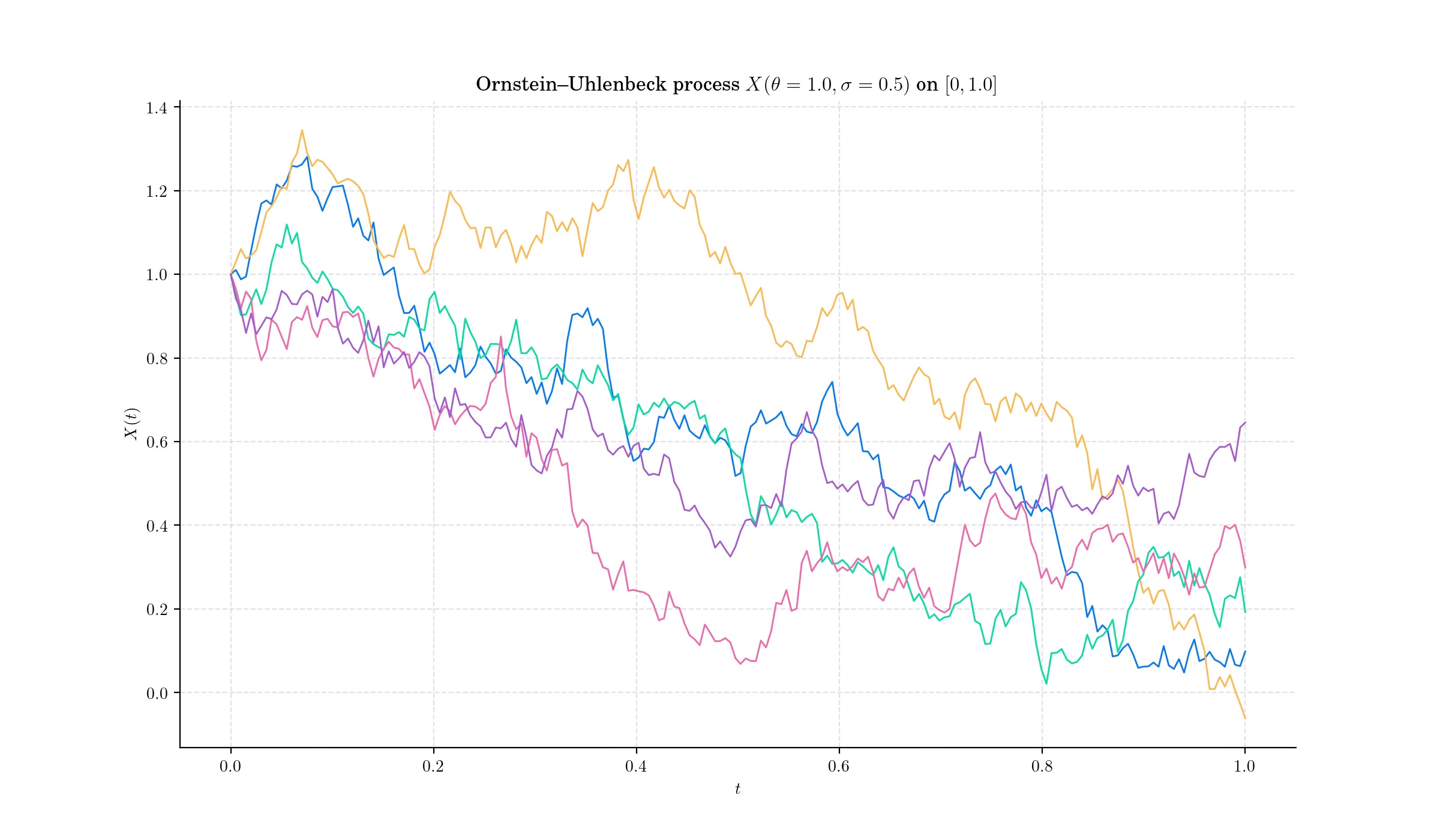
Definition#

The Ornstein–Uhlenbeck process \(X=\{X(t) : t\geq 0\}\) is defined by the following stochastic differential equation:

\[dX\_t = -\theta X\_t dt + \sigma dW\_t, \qquad t\geq 0,\]

with initial condition \(X(0) = x\_0\); where \(\theta>0\) and \(\sigma >0\) are constant parameters and \(W\) denotes the Wiener process. In order to find the solution to this SDE, let us set the function \(f(t,x) = x e^{\theta t}\). Then, Ito’s formula implies

\[ X\_te^{\theta t} = x\_0 +\int\_0^t X\_s \theta e^{\theta s}ds + \int\_0^t e^{\theta s}dX\_s \]
\[= x\_0 + \int\_0^t \left\[ \theta X\_s e^{\theta s} - \theta e^{\theta s} X\_s\right\] ds + \int\_0^t e^{\theta s}\sigma dW\_s\]
\[= x\_0 + \int\_0^t e^{\theta s}\sigma dW\_s\]

Thus

\[X\_t = x\_0e^{-\theta t} + \sigma \int\_0^t e^{-\theta (t-s)}dW\_s, \]

This expression implies that for each \(t>0\), the random variable \(X\_t\) follows a normal distribution –since it can be expressed as the sum of a deterministic part and the integral of a deterministic function with respect to the Brownian motion.

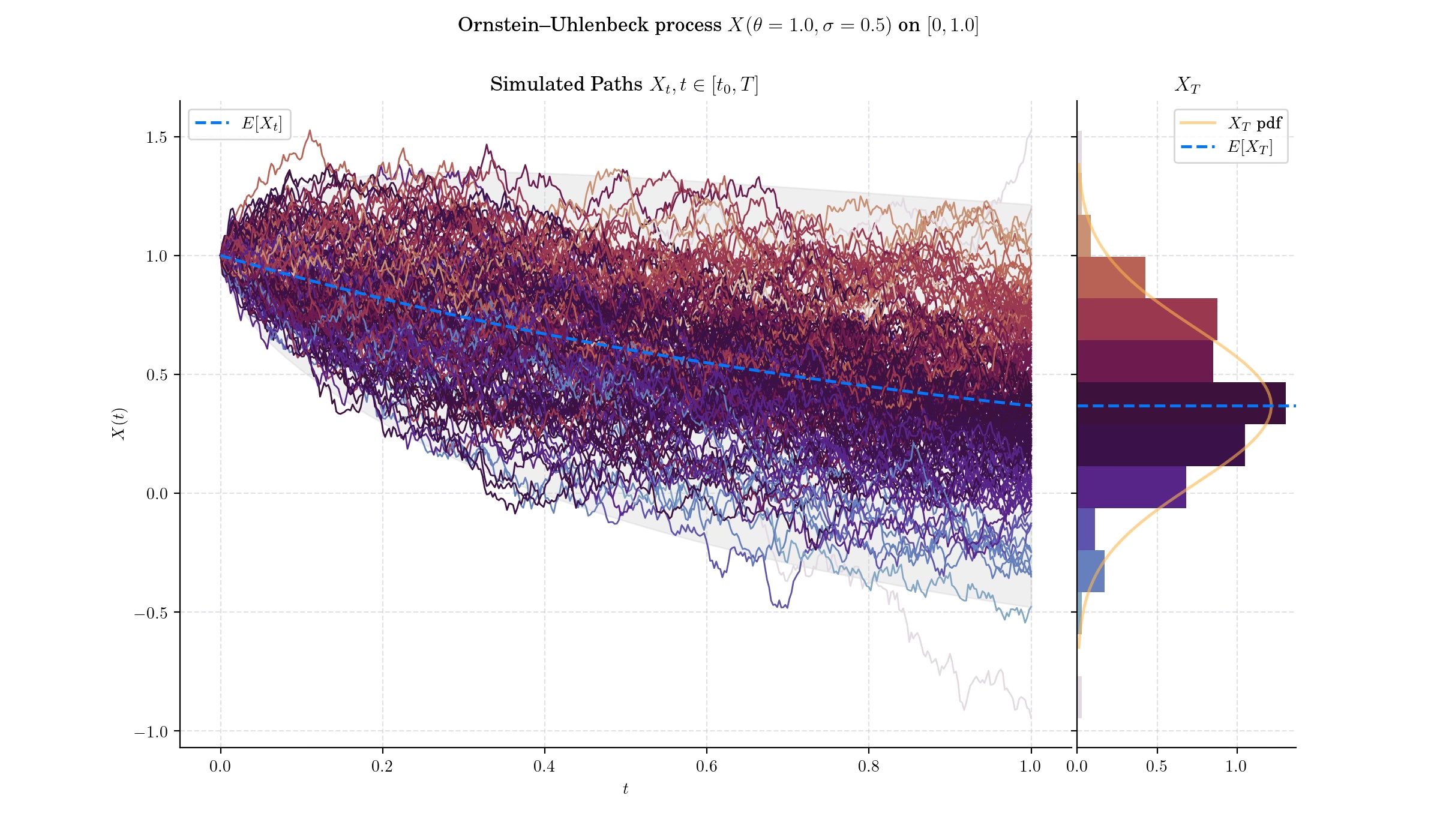
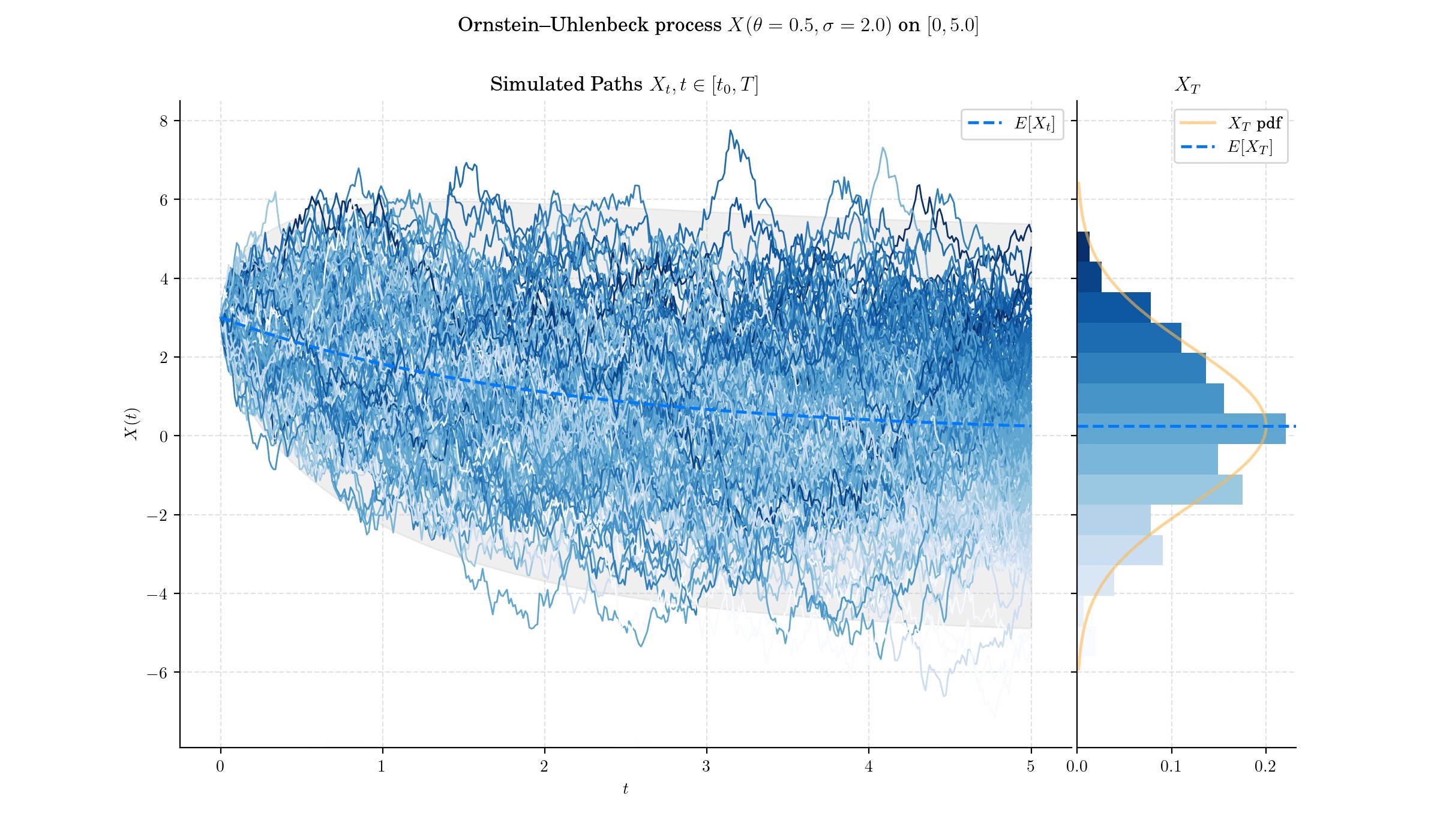
đź”” Random Facts đź””#

  • The process was introduced by physicists  Leonard Ornstein and George Eugene Uhlenbeck in 1930 to describe the velocity of a massive particle undergoing Brownian motion in a viscous fluid.

  • The Ornstein–Uhlenbeck process is a stationary Gauss–Markov process, which means that it is a Gaussian process, a Markov process, and is temporally homogeneous. In fact, it is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables.

  • The Ornstein–Uhlenbeck process can also be considered as the continuous-time analogue of the discrete-time AR(1) process.

  • The Ornstein–Uhlenbeck process can also be described in terms of a probability density function, \(f(x,t),\) which specifies the probability of finding the process in the state \(x\) at time \(t\). This function satisfies the Fokker–Planck equation

\[ \frac{\partial f}{\partial t} = \theta \frac{\partial}{\partial x} (x f) + \frac{\sigma^2}{2} \frac{\partial^2f}{ \partial x^2}.\]

  • The Ornstein–Uhlenbeck process (and its variations) is widely used to model interest rates, currency exchange rates, and commodity prices.

More to Read đź“š#

  • Doob, J. L. “The Brownian Movement and Stochastic Equations.” Annals of Mathematics, vol. 43, no. 2, 1942, pp. 351–69. JSTOR, https://doi.org/10.2307/1968873. Accessed 12 Dec. 2024.

  • Jacobsen, Martin. “Laplace and the Origin of the Ornstein-Uhlenbeck Process.” Bernoulli, vol. 2, no. 3, 1996, pp. 271–86. JSTOR, https://doi.org/10.2307/3318524. Accessed 12 Dec. 2024.

  • Risken, H. (1989). The Fokker–Planck Equation: Methods of Solution and Applications. New York: Springer-Verlag. ISBN 978-0387504988.

  • Patrick Cheridito. Hideyuki Kawaguchi. Makoto Maejima. “Fractional Ornstein-Uhlenbeck processes.”Electron. J. Probab. 8 1 - 14, 2003. https://doi.org/10.1214/EJP.v8-125

P.s. If you are curious about probability distributions visit the Advent Calendar 2023 ✨

Contents