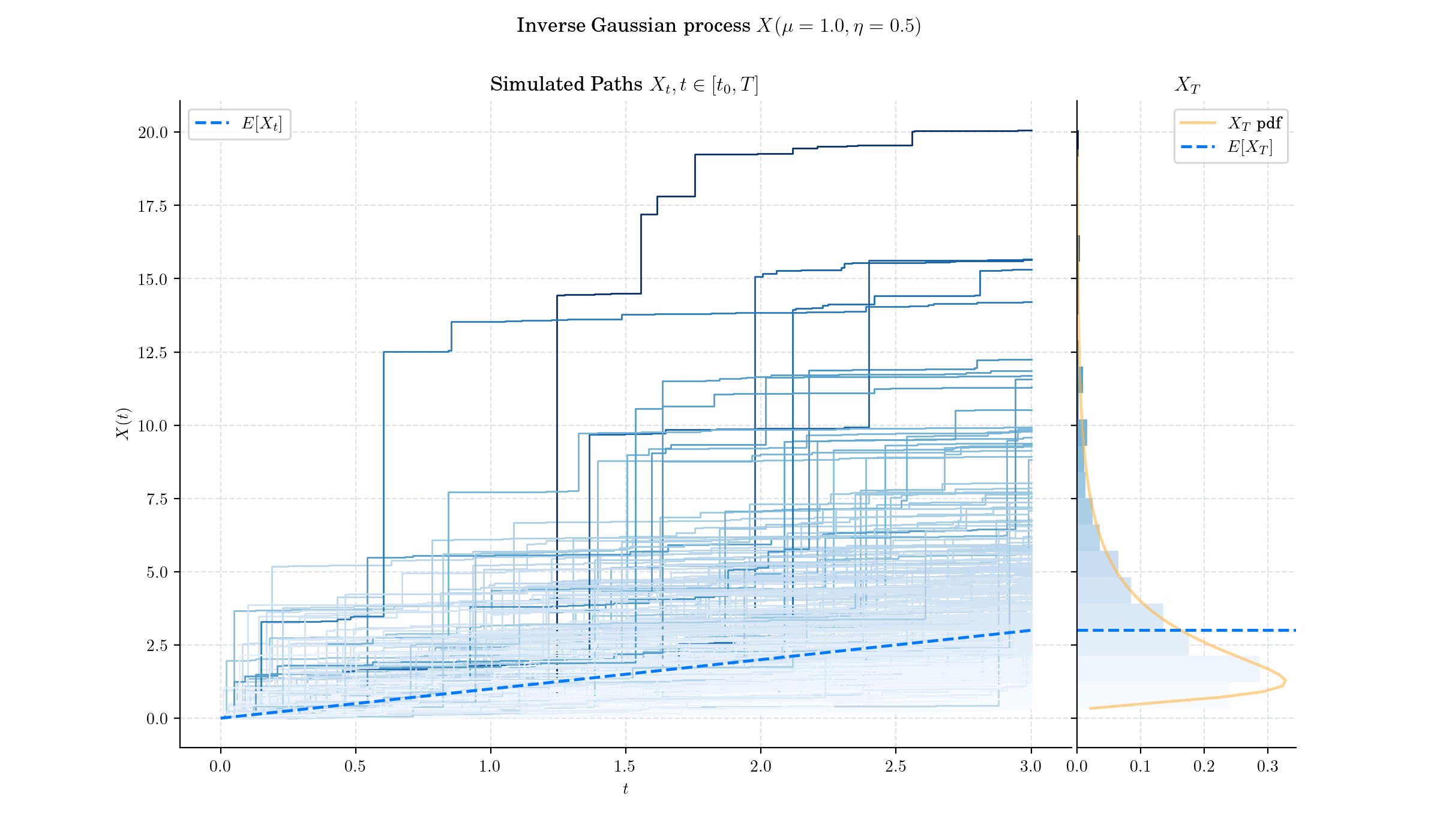
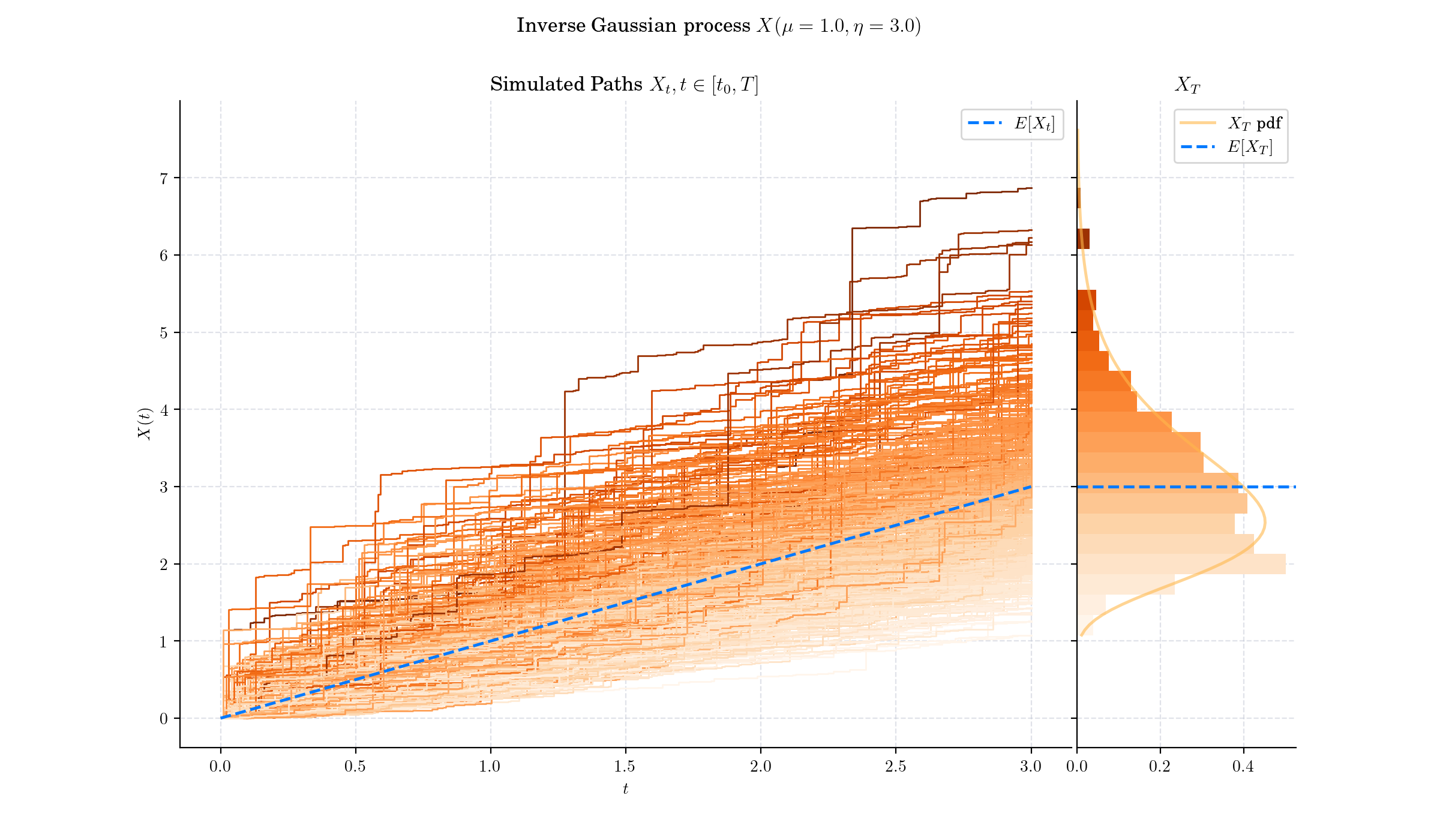
Day 23: Inverse Gaussian Process

The Inverse Gaussian Process is a stochastic process whose increments follow the Inverse Gaussian distribution, a continuous probability distribution often used to model positive, skewed data. This process is widely applied in fields such as finance, reliability engineering, and queueing theory.

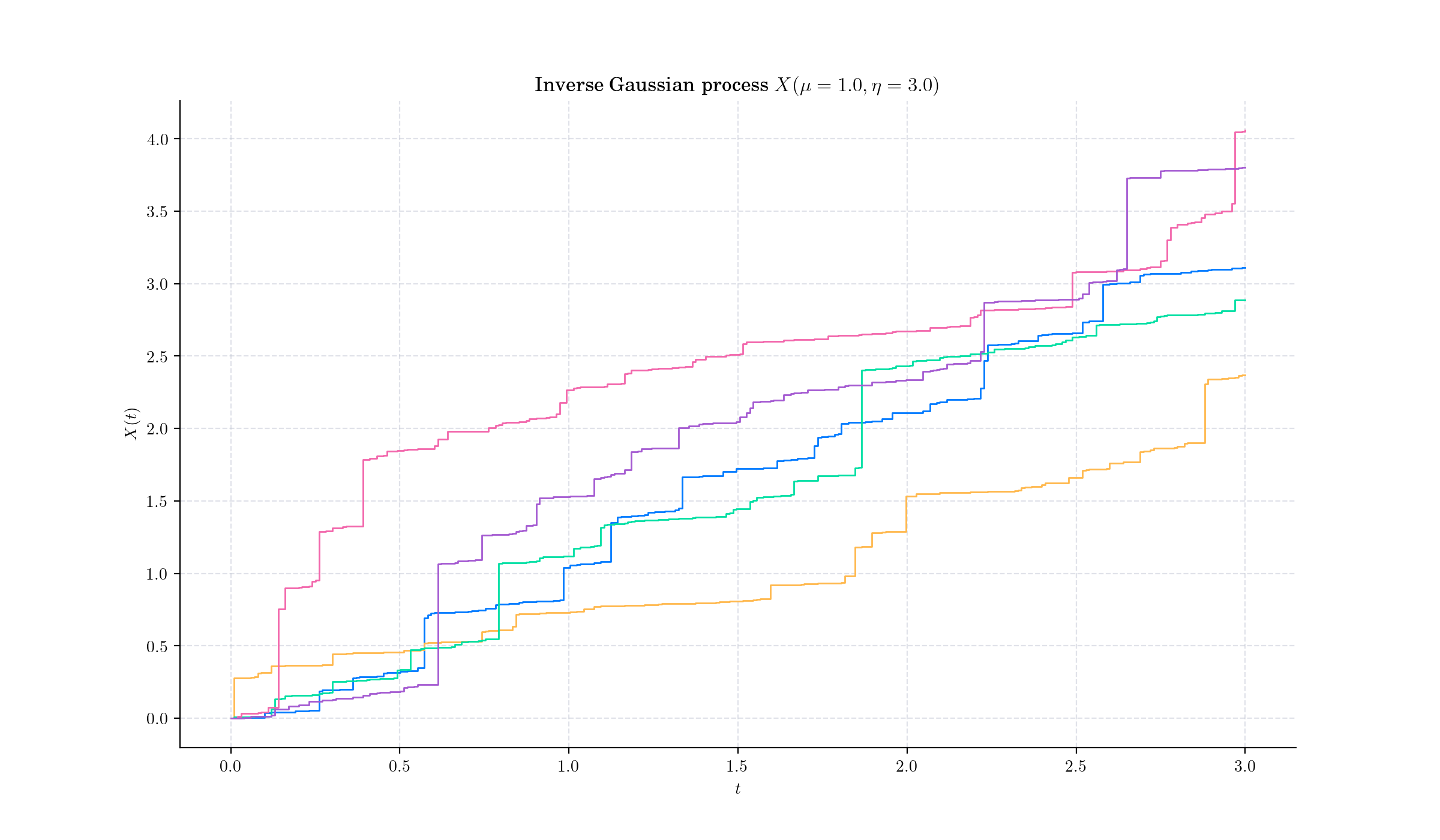
Definition

An Inverse Gaussian process is a stochastic process \(\{X(t),t\geq 0\}\) where:

• \(X(0)=0\),

• The increments \(X(t)−X(s)\) (for t>s) are independent and follow the Inverse Gaussian distribution with mean \(\mu(t-s)\) and scale parameter \(\eta\),

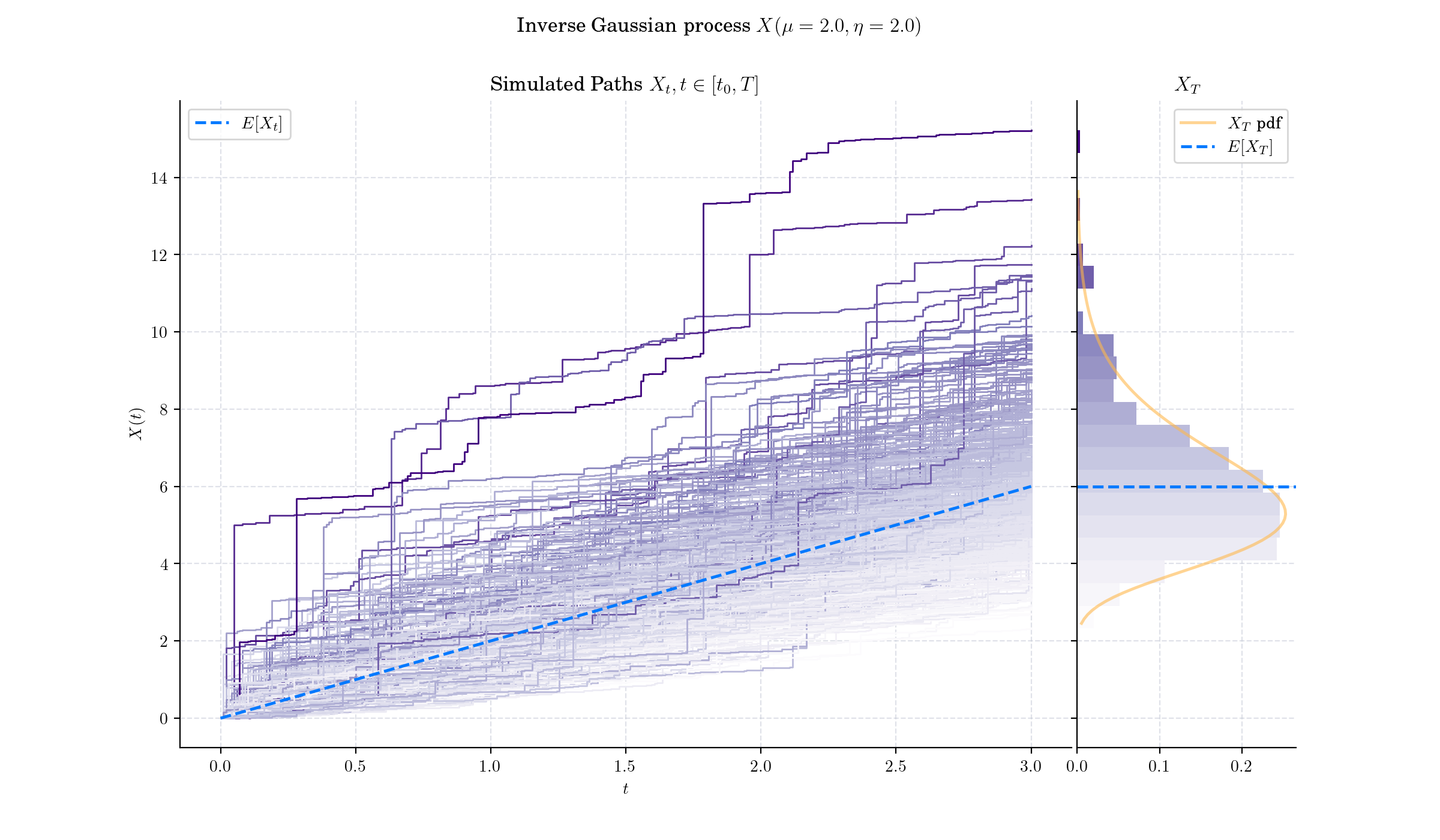
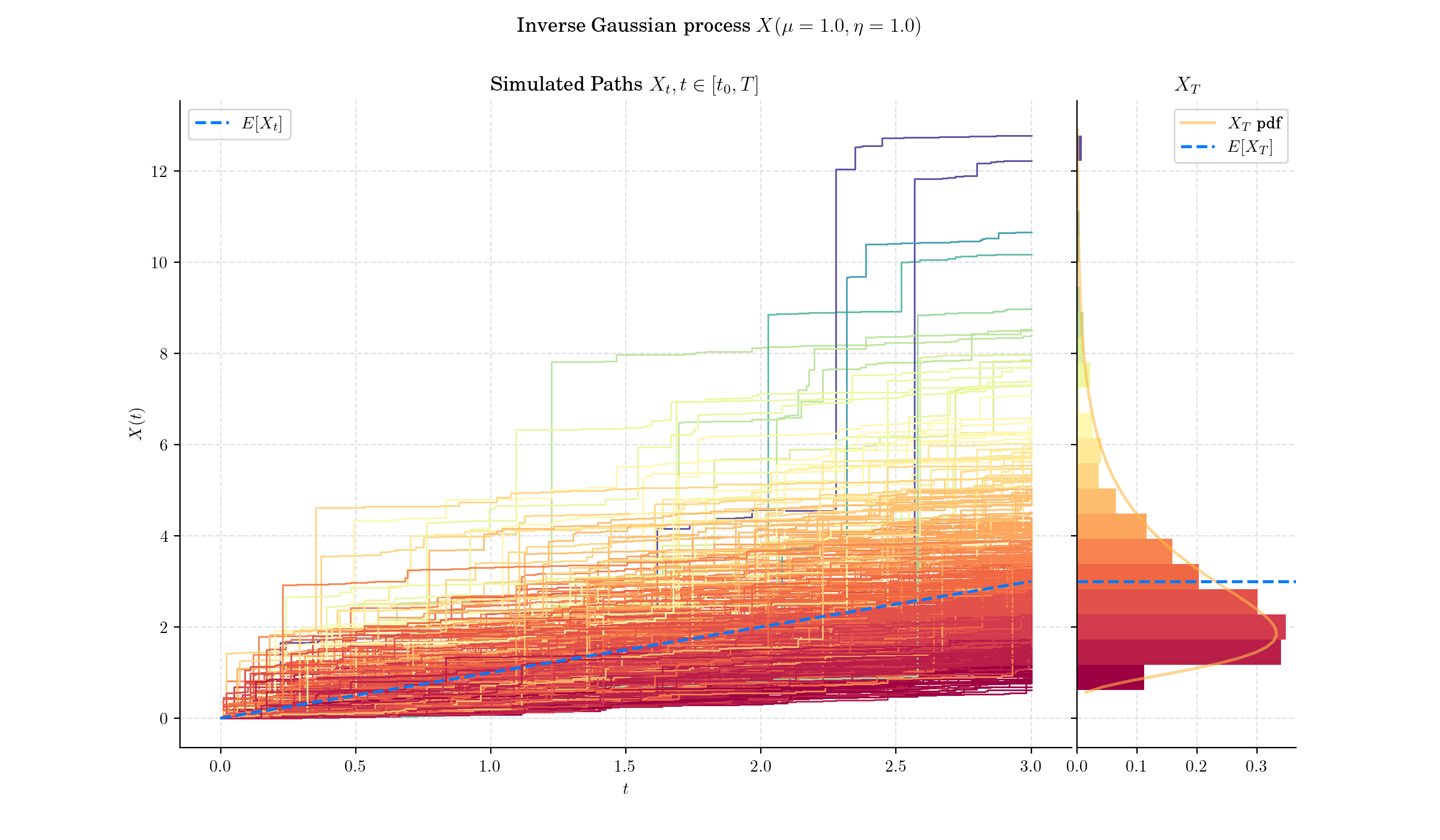
🔔 Random Facts 🔔

• This Inverse Gaussian distribution appears to have been first derived in 1900 by Louis Bachelier as the time a stock reaches a certain price for the first time. In 1915 it was used independently by Erwin Schrödinger and Marian v. Smoluchowski as the time to first passage of a Brownian motion.

• The name inverse Gaussian was proposed by British medical physicist and statistician Maurice Tweedie in 1945

• In 1968, M. T. Wasan introduced the concept of the Inverse Gaussian process in his paper “On an Inverse Gaussian Process,” published in the Scandinavian Actuarial Journal. Wasan’s work laid the foundation for subsequent research into the Inverse Gaussian process, influencing studies in areas such as bivariate distributions and first-passage time distributions in stochastic processes.

• The Inverse Gaussian process is used in various fields to model cumulative or first-passage phenomena where skewed, positive increments are observed

More to Read 📚

• TWEEDIE, M. Inverse Statistical Variates. Nature 155, 453 (1945). https://doi.org/10.1038/155453a0

• Wasan, M. T. (1968). On an inverse Gaussian process. Scandinavian Actuarial Journal, 1968(1–2), 69–96. https://doi.org/10.1080/03461238.1968.10413264

• Wang, X., & Xu, D. (2010). An Inverse Gaussian Process Model for Degradation Data. Technometrics, 52(2), 188–197. https://doi.org/10.1198/TECH.2009.08197

P.s. If you are curious about probability distributions visit the Advent Calendar 2023 ✨