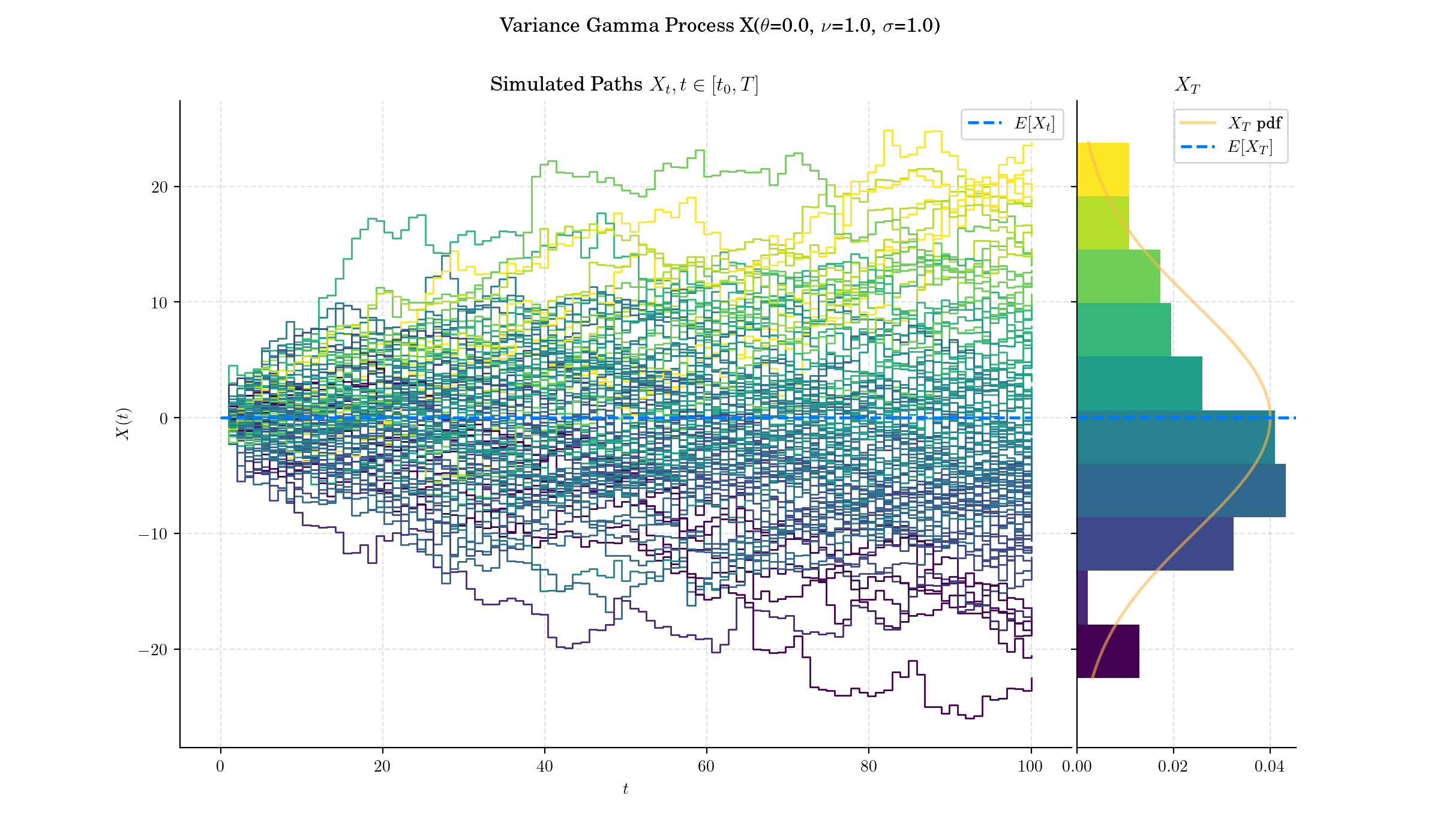
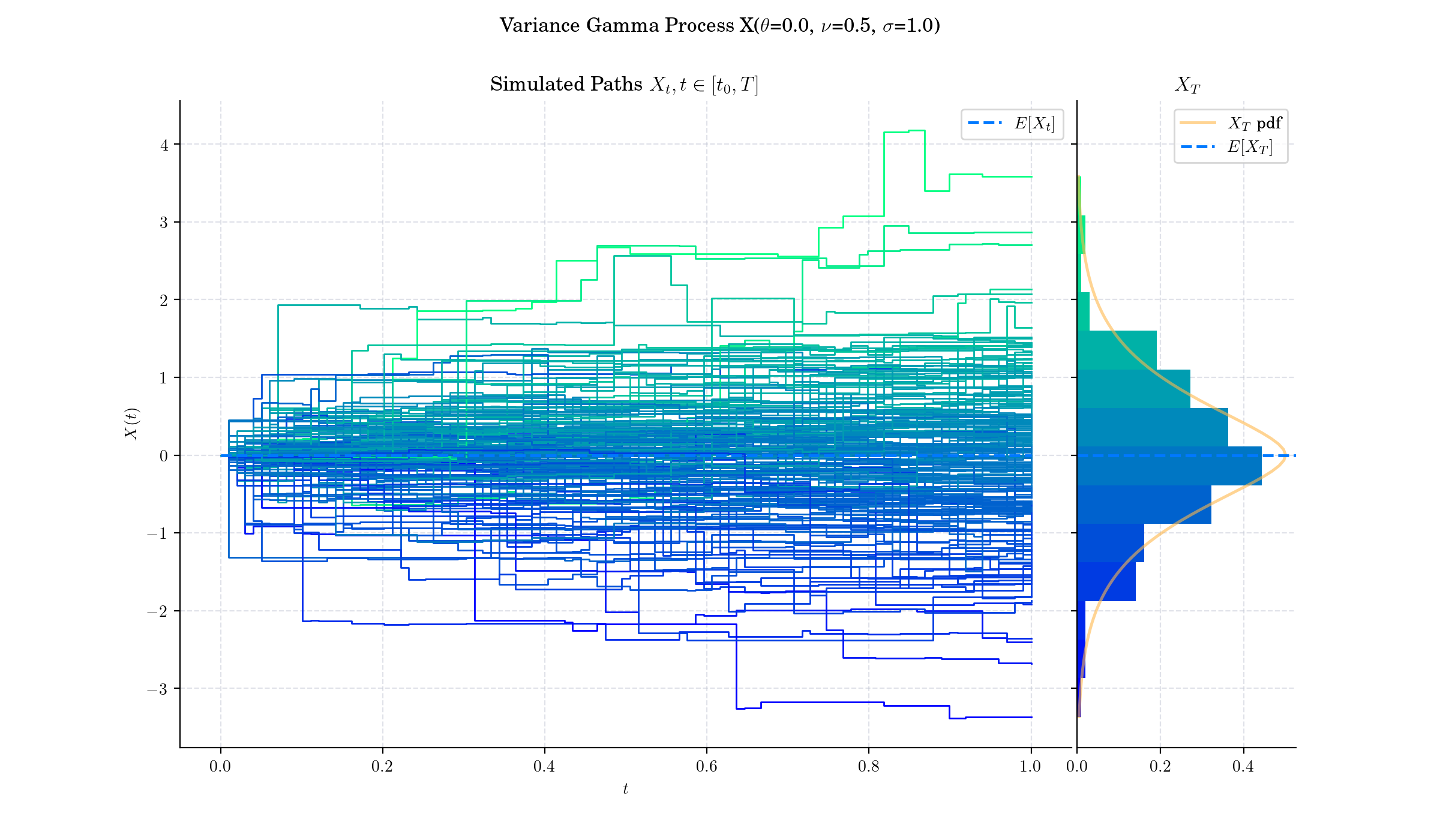
Day 21: Variance Gamma Process#

In the theory of stochastic processes the Variance Gamma(VG) process, also known as Laplace motion or Madan-Seneta process, is a Lévy process determined by a random time change.

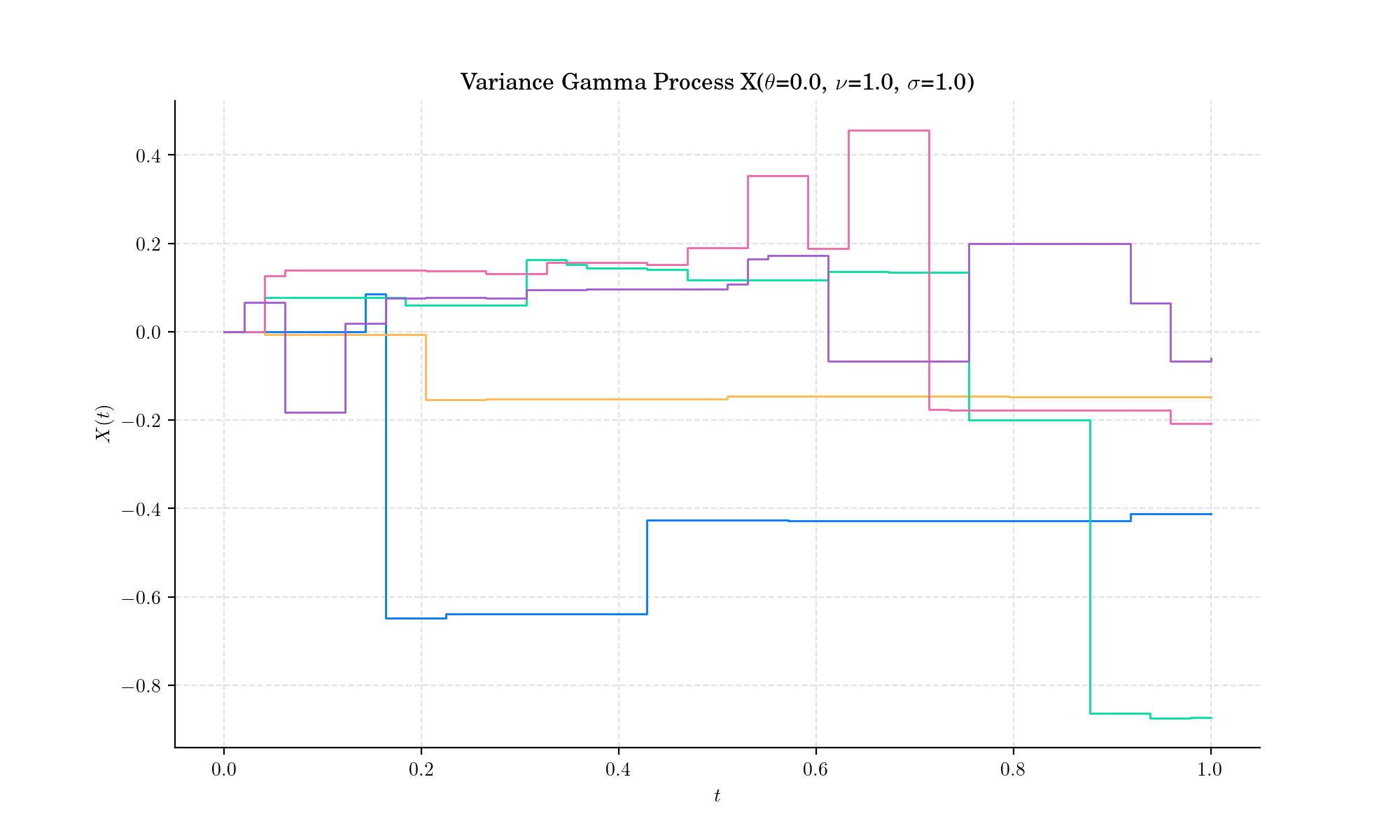
Definition#

There are several representations of the Variance-Gamma process that relate it to other processes. It can for example be written as a Brownian motion \(W\) with drift \(\theta t\) subjected to a random time change which follows a gamma process \(\Gamma(t;1,\nu)\), i.e.:

\[X(t; \sigma, \nu, \theta) = \theta \Gamma(t;1, \nu) + \sigma W(\Gamma(t;1, \nu)); \quad t\geq 0.\]

There is no diffusion component in the VG process and it is thus a pure jump process. The increments are independent and follow a variance-gamma distribution, which is a generalisation of the Laplace distribution.

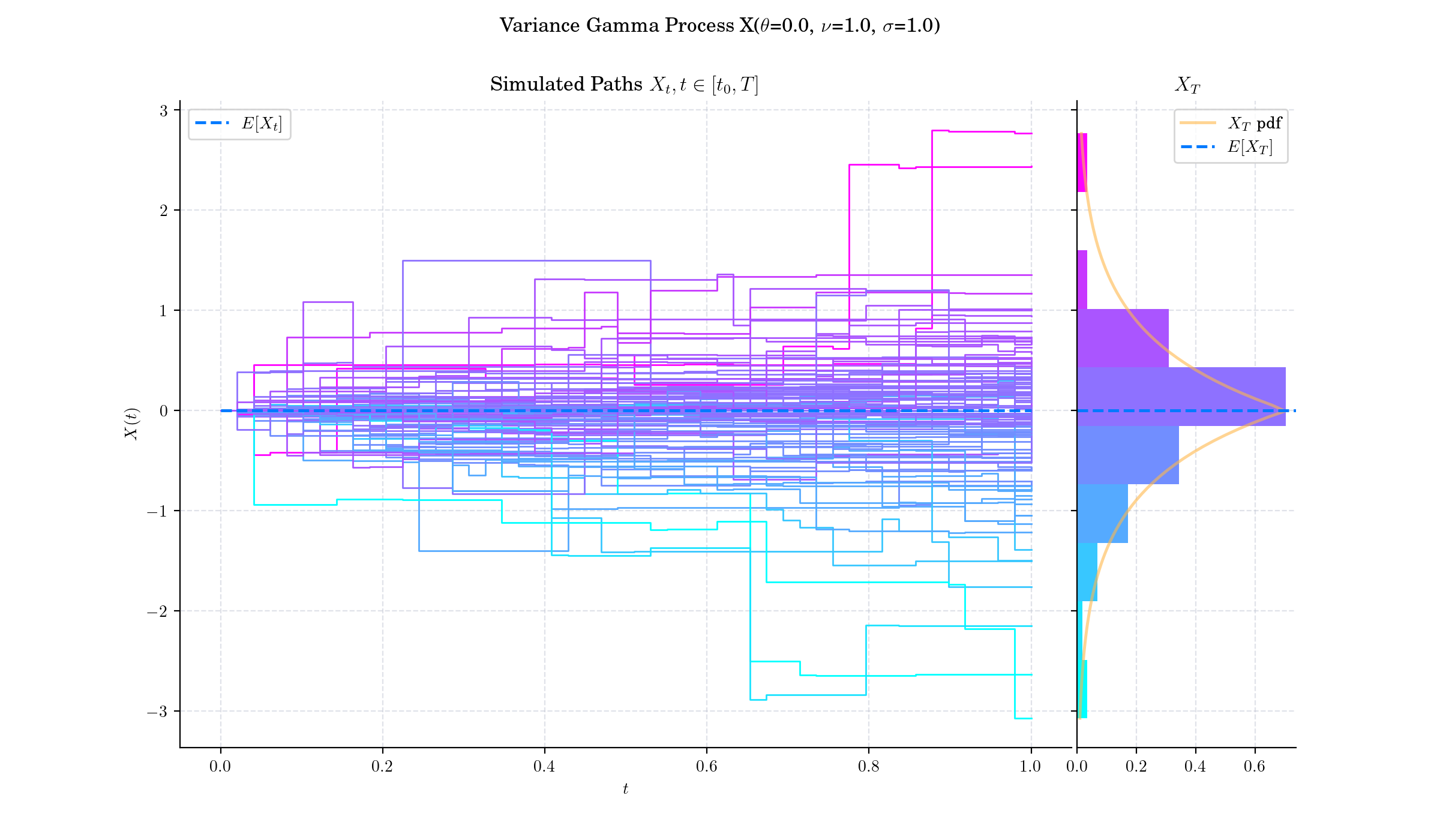
🔔 Random Facts 🔔#

The Variance-Gamma process was introduced by mathematicians Dilip Madan and Eugene Seneta in 1990 as a model for stock price returns. They aimed to address the deficiencies of the Black-Scholes model, which assumes normally distributed returns, by introducing skewness and excess kurtosis into the framework.
Madan and Seneta initially presented the case of symmetric distributed increments (\(\theta=0\)), which was extended to incorporate skewness (\(\theta\in\mathbb{R}\)) by Madan, Carr and Chang who extended the model to allow for an asymmetric form and present a formula to price European options under the variance gamma process.
The Variance-Gamma process builds on earlier work on Lévy processes and time-changed Brownian motions. It became popular in financial modelling due to its ability to fit empirical return distributions better than traditional Gaussian models.
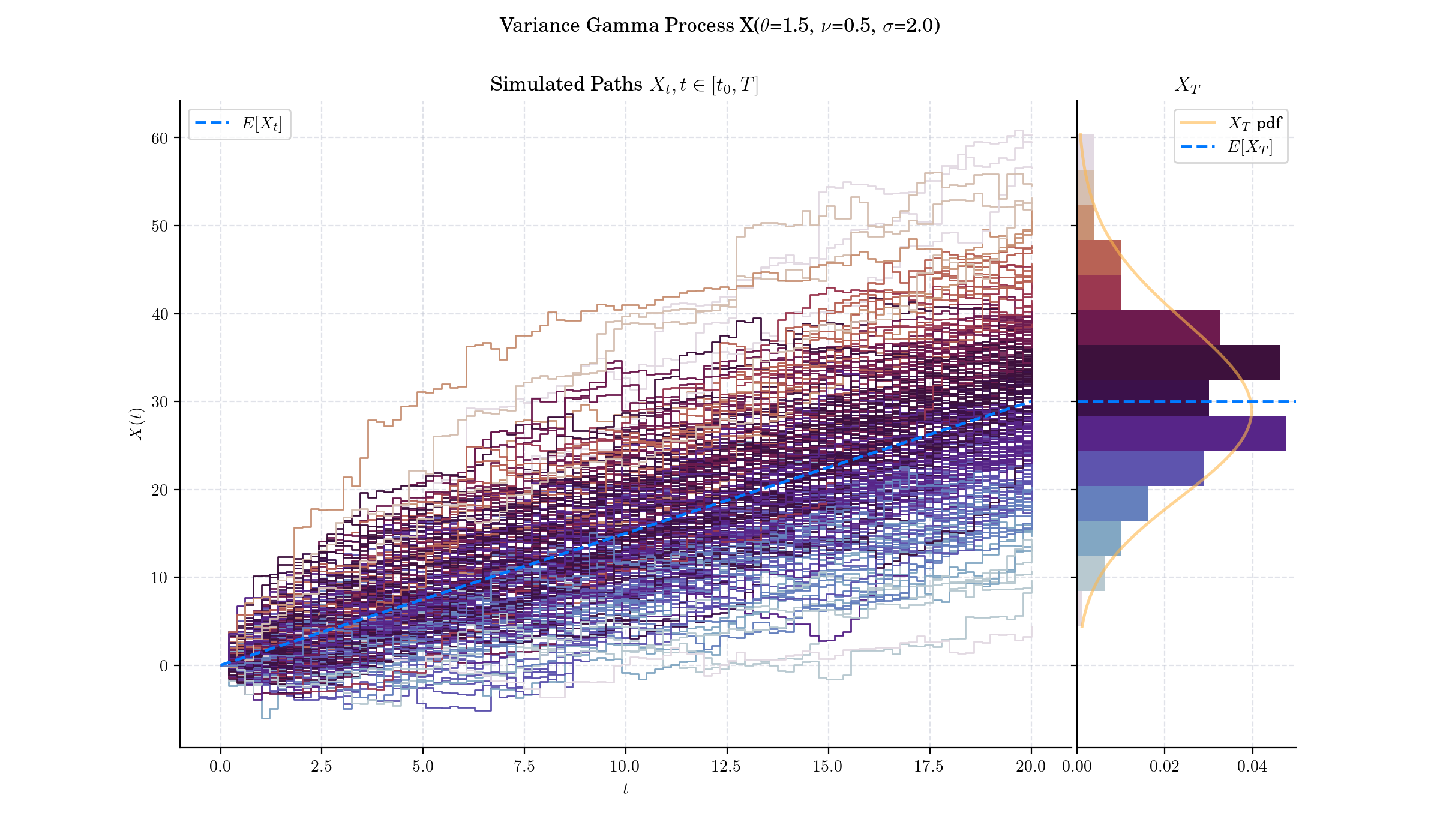
The Variance-Gamma process has finite moments, distinguishing it from many Lévy processes.
The VG process can be advantageous to use when pricing options since it allows for a wider modeling of skewness and kurtosis than the Brownian motion does. As such the variance gamma model allows to consistently price options with different strikes and maturities using a single set of parameters.

Day 21: Variance Gamma Process

Contents

Day 21: Variance Gamma Process#

Definition#

🔔 Random Facts 🔔#

More to Read 📚#