Day 16: CIR Process#

The Cox-Ingersoll-Ross (CIR) model is a widely-used mathematical framework for modelling the evolution of interest rates over time. It is a type of “one factor model” (short-rate model) as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives.

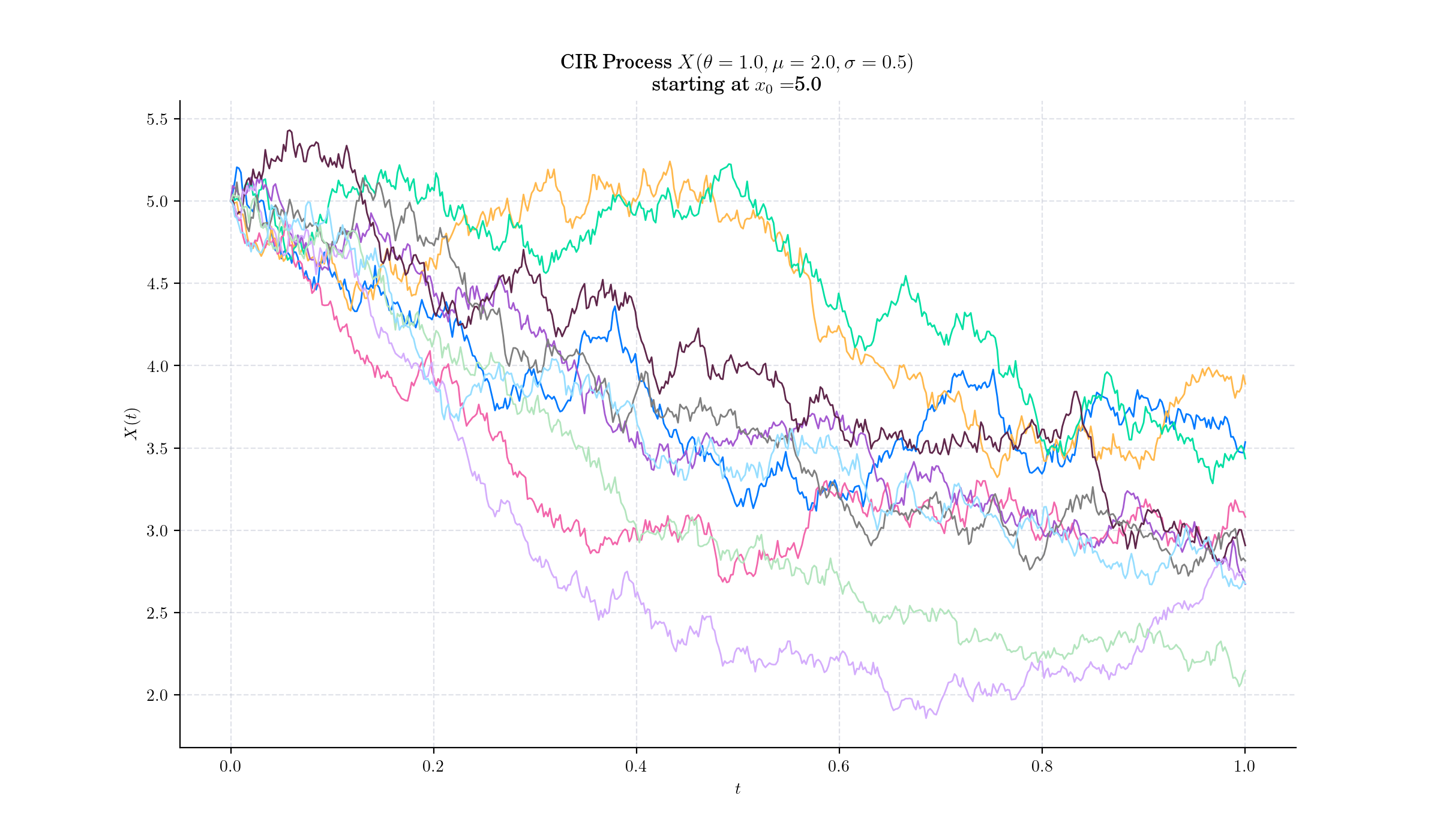
Definition#

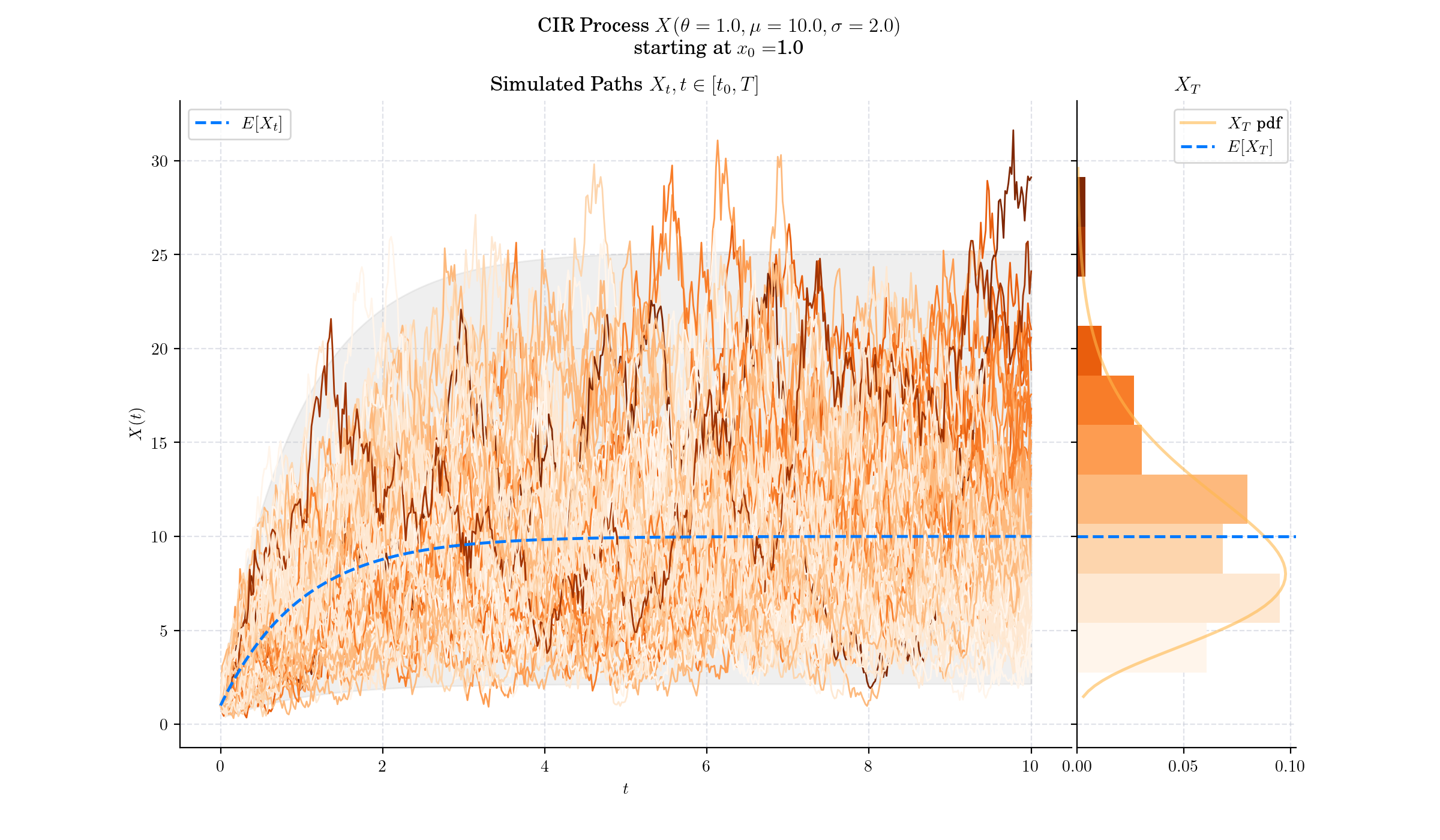
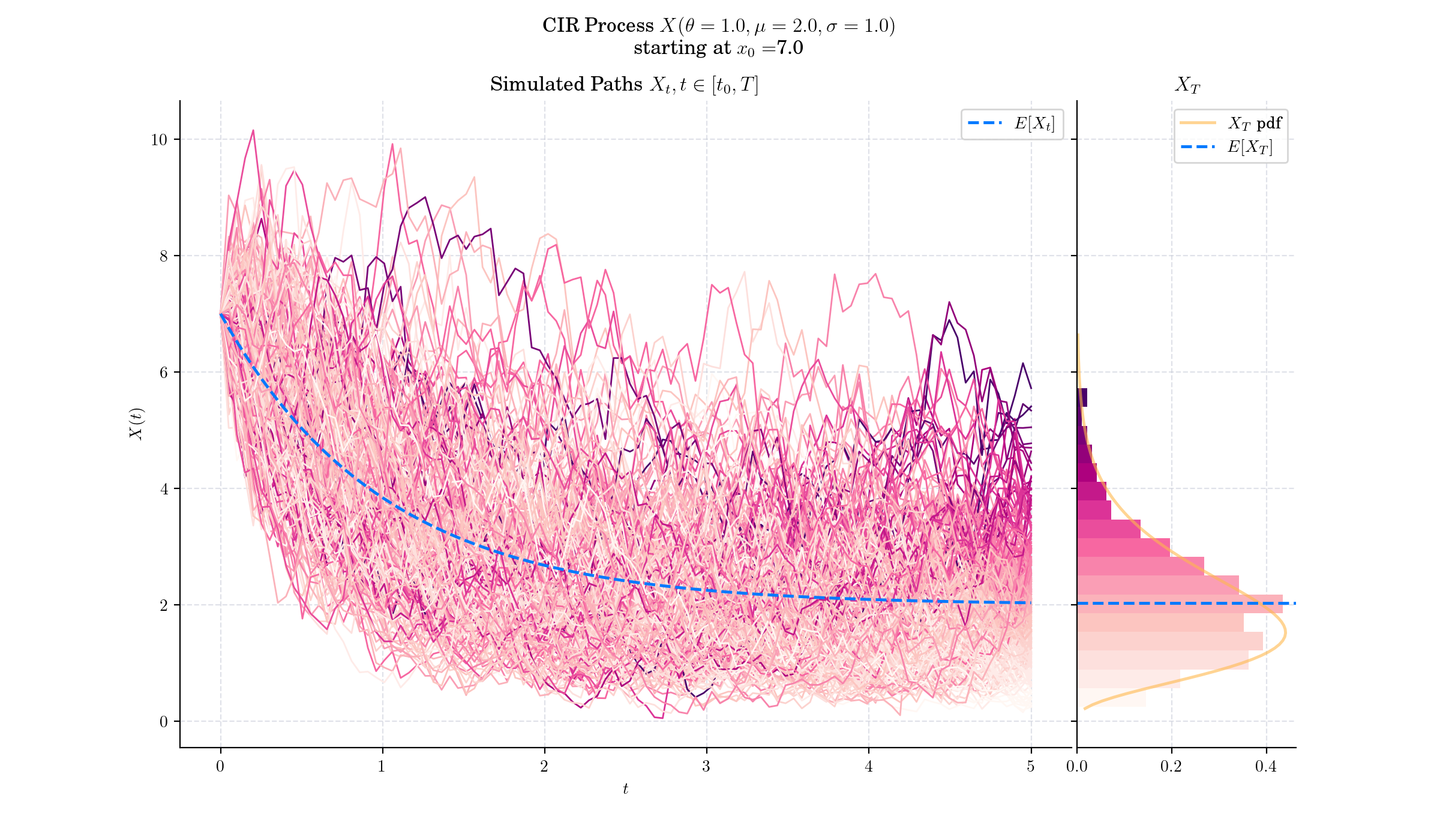
The Cox-Ingersoll-Ross (CIR) model describes the dynamics of interest rates via a stochastic process which can be defined by the following Stochastic Differential Equation (SDE)

\[dX\_t = \theta (\mu - X\_t) dt + \sigma \sqrt{X\_t} dW\_t, \quad t >0,\]

with initial condition \(X\_0 =x\_0\in\mathbb{R}\), and where \(W\_t\) is a standard Brownian motion, and the three parameters are constants:

\(\theta>0\) : speed or mean reversion coefficient
\(\mu >0\) : long term mean
\(\sigma>0\) : volatility.

🔔 Random Facts 🔔#

The CIR model was introduced in 1985, by economists John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model, in their seminal paper “A Theory of the Term Structure of Interest Rates”
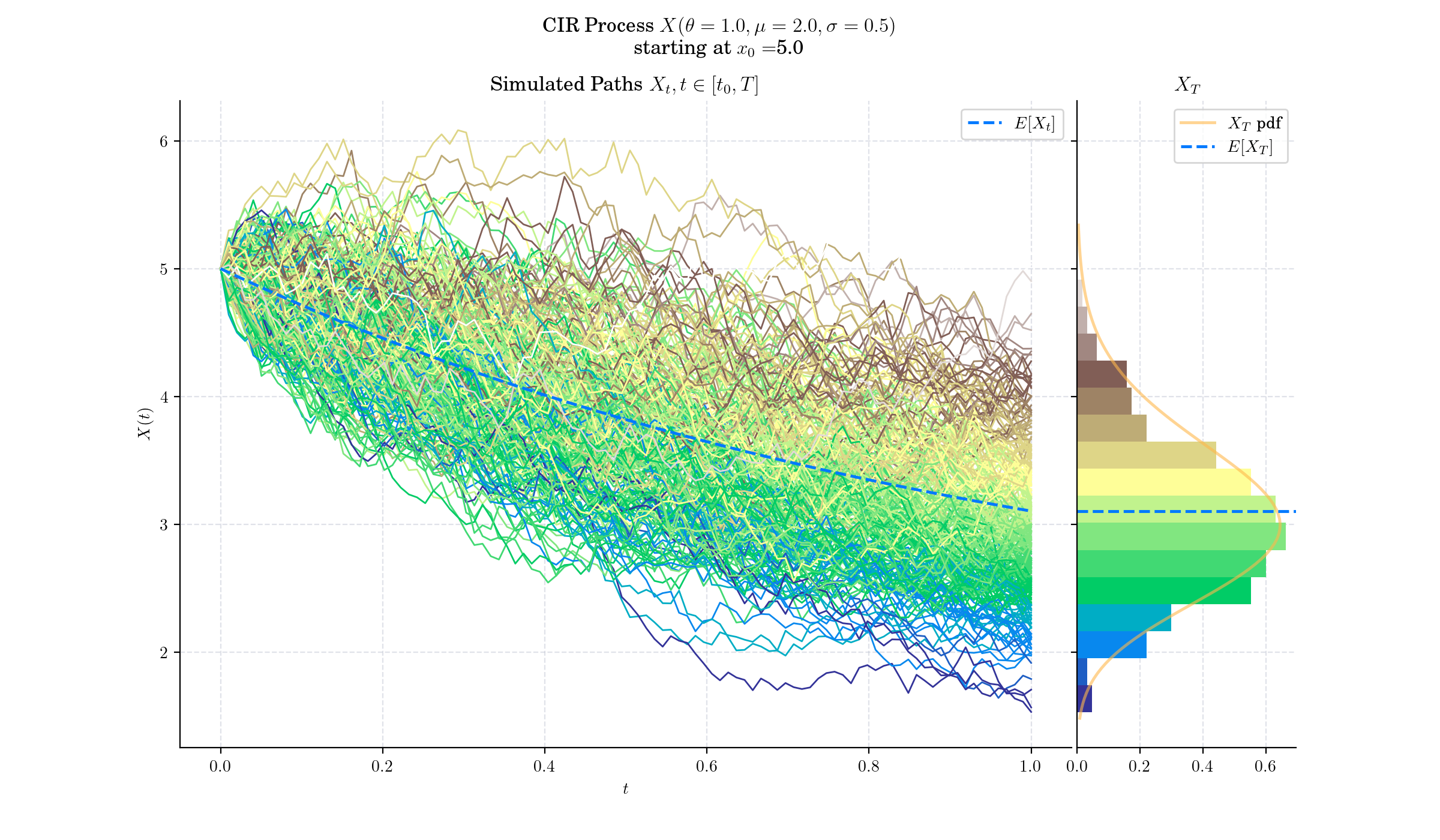
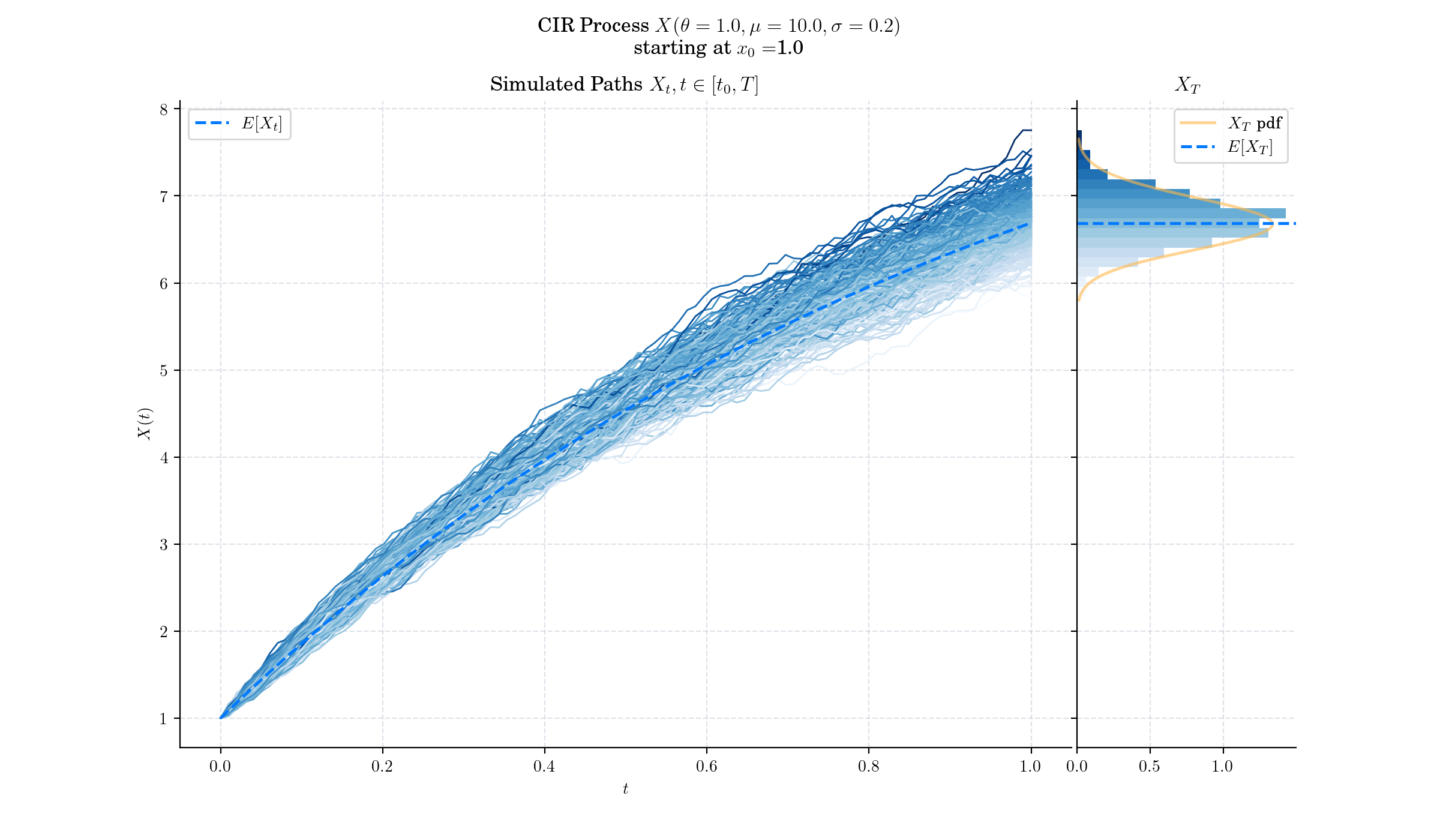
The standard deviation factor in the SDE avoids the possibility of negative interest rates for all positive values of \(\theta\) and \(\mu\). An interest rate of zero is also precluded if the so-called Feller condition \(2\theta\mu \geq \sigma^2\), is met.
The drift factor \(\theta(\mu-X\_t)\), is exactly the same as in the Vasicek model. It ensures mean reversion of the interest rate towards the long run value \(\mu\), with speed of adjustment governed by the strictly positive parameter \(\theta\).
The CIR model allows for closed-form solutions for certain financial instruments, such as zero-coupon bond prices and some interest rate derivatives, making it practical for use in finance.
The CIR process is a Bessel Squared process transformed by a space-time change

Day 16: CIR Process

Contents

Day 16: CIR Process#

Definition#

🔔 Random Facts 🔔#

More to Read 📚#