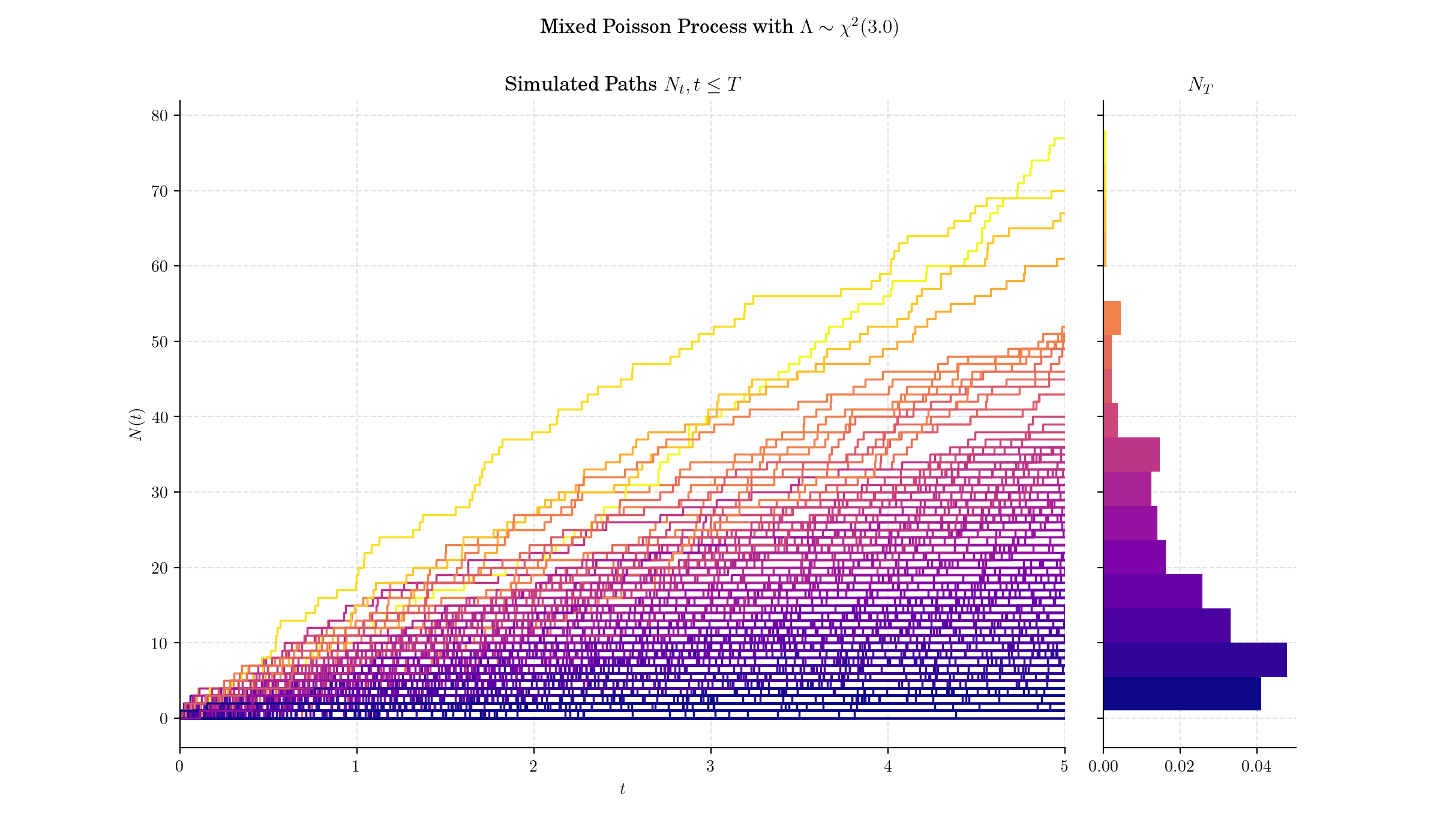
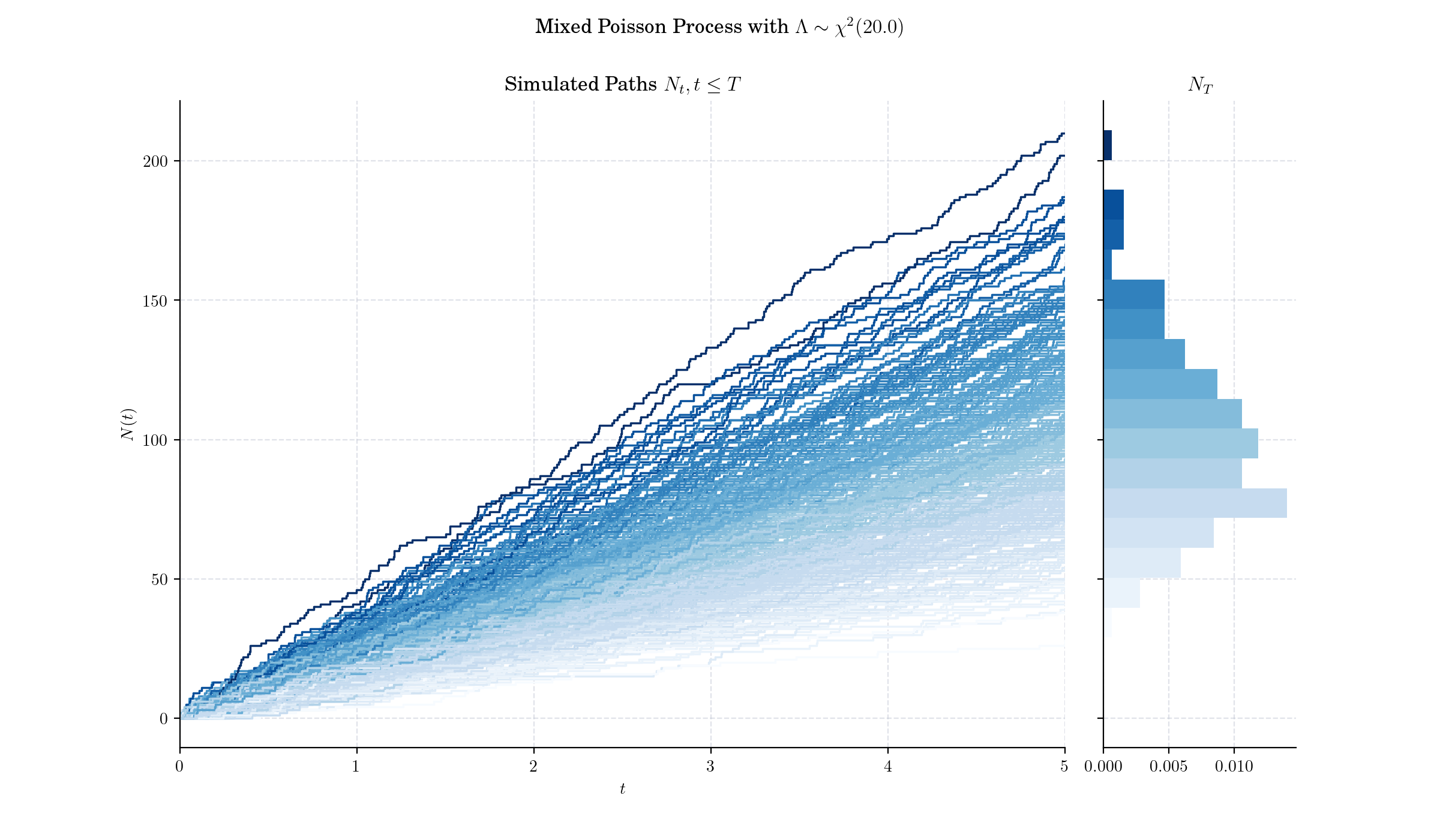
Day 15: Mixed Poisson Process#

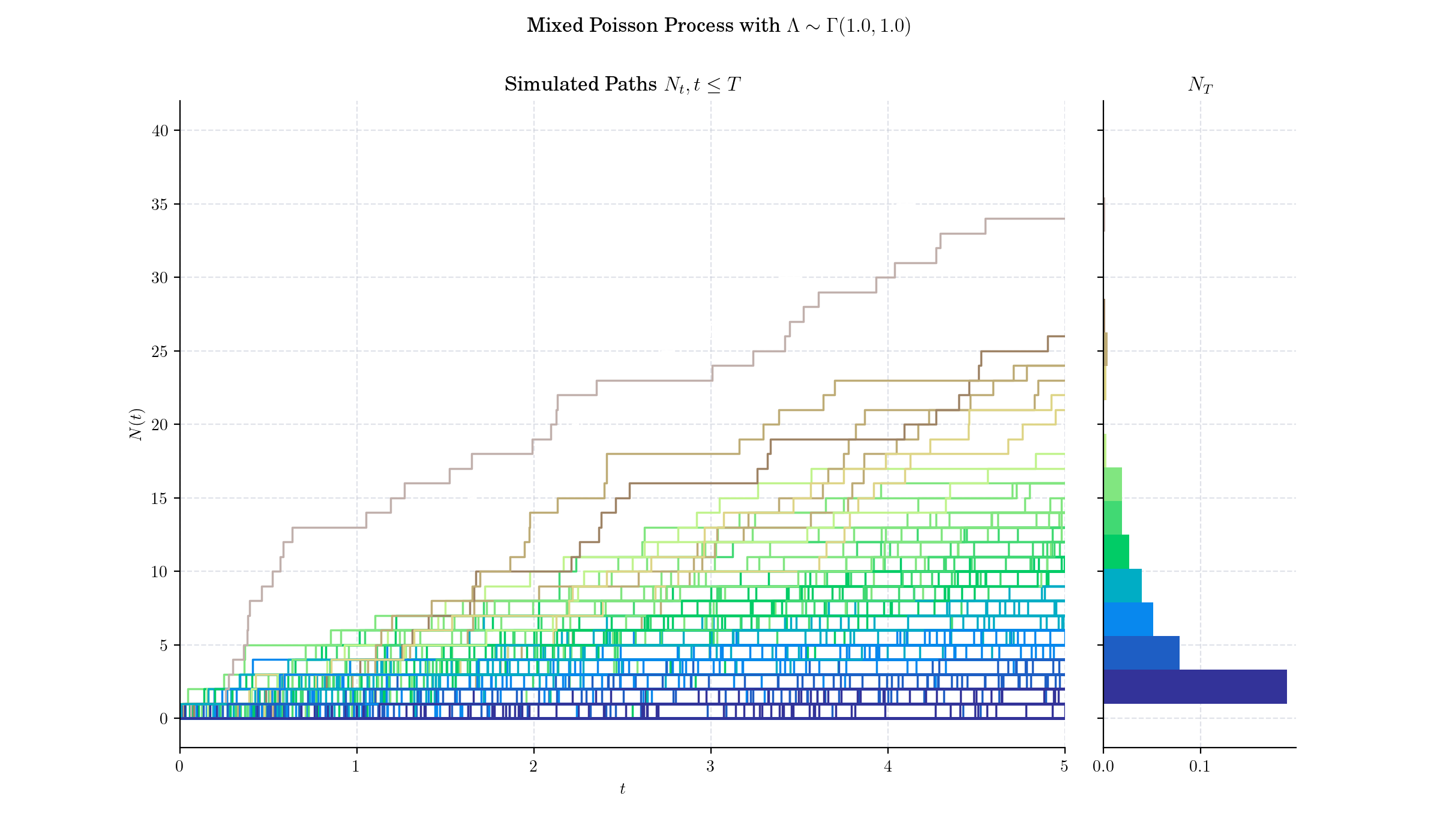
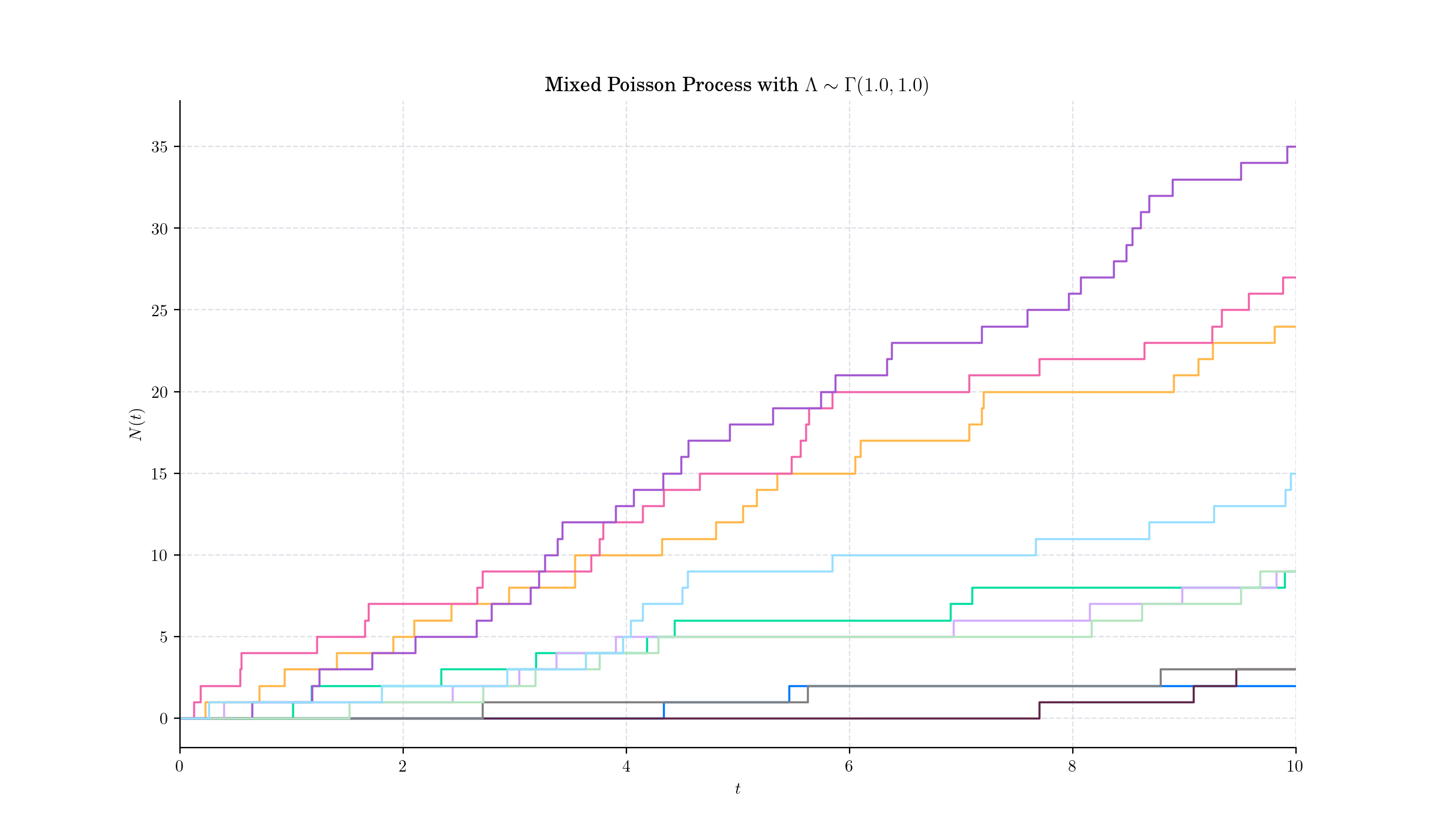
The Mixed Poisson Process (MPP) is an extension of the classical Homogeneous Poisson process that incorporates randomness into the rate parameter \(\lambda\). In a standard homogeneous Poisson process, the rate parameter \(\lambda\) is constant, and events occur independently over time or space. In contrast, a Mixed Poisson Process assumes \(\lambda\) is itself a random variable governed by a specified distribution.

Definition (on the real-line)#

A Mixed Poisson process (MPP) \(\{N(t), t\in \[0, \infty)\}\) is a counting process with counting distribution of the form:

\[P(N(t)= n) = \int\_0^{\infty} \frac{1}{n!} e^{-\lambda t} (\lambda t)^n d \Lambda(\lambda), \qquad n\in \mathbb{N},\]

where \(\Lambda\) is the structure distribution given by \(\Lambda(\lambda) = P(\Lambda \leq \lambda)\) with \(\Lambda(0)=0\). This type of distribution is known as mixed Poisson distribution which gives the name to the processes.

Note that if \(\Lambda\) has density function \(g\), we have

\[P(N(t)= n) = \int\_0^{\infty} \frac{1}{n!} e^{-\lambda t} (\lambda t)^n g(\lambda) d\lambda, \qquad n\in \mathbb{N}.\]

Thus, given \(\Lambda = \lambda\), \(N(t)\) follows a Poisson distribution with parameter \(\lambda t\), i.e.:

\[P\left(N(t)= n| \Lambda=\lambda\right) = \frac{1}{n!} e^{-\lambda t} (\lambda t)^n, \qquad n\in\mathbb{N}.\]

🔔 Random Facts 🔔#

Mixed Poisson processes were first introduced in 1938 by French mathematician J. Dubourdieu, who wanted to describe the number of claims, in fixed periods, occurring in sickness and accident insurance
If the intensity random variable \(\Lambda\) is degenerate at a constant \(\lambda\) (\(\lambda > 0\)), then we have the Homogeneous Poisson process. This is the only MPP that is simultaneously a renewal process.
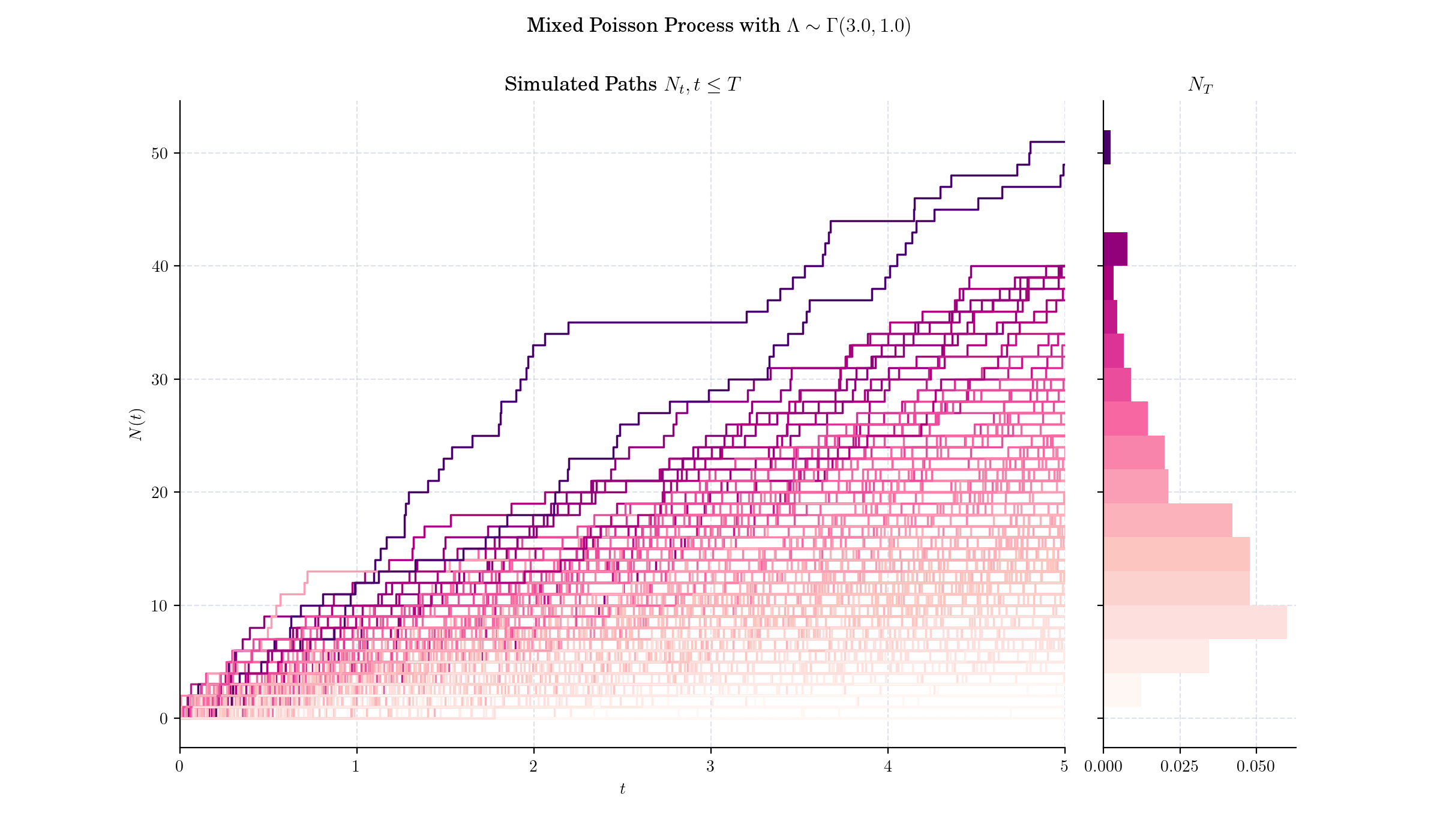
If the intensity random variable \(\Lambda\) follows a Gamma distribution, then the resulting counting process \(N(t)\) follows a Pascal or negative Binomial distribution. This case is known as the Pascal or Polya process.
The Mixed Poisson Process is a specific case of a Cox Process, also known as a doubly stochastic Poisson process. The Cox process generalises the Poisson process even further by allowing the intensity/rate to vary over time according to an underlying stochastic process

Day 15: Mixed Poisson Process

Contents

Day 15: Mixed Poisson Process#

Definition (on the real-line)#

🔔 Random Facts 🔔#

More to Read 📚#