Day 24: Fractional Brownian motion

Day 24: Fractional Brownian motion#

Fractional Brownian Motion (fBm) is a generalisation of classical Brownian motion introduced to model complex phenomena exhibiting long-range dependence and self-similarity. Since its inception, fBm has become a cornerstone in fields like finance, physics, and telecommunications.

Definition#

The fractional Brownian motion (fBM) is a continuous-time Gaussian process \(B\_H(t)\) on \(\[0,T\]\) that starts at zero, has expectation zero for all \(t\) in \(\[0,T\]\), and has the following covariance function:

\[E\left\[B\_H(t) B\_H(s) \right\] = \frac{1}{2}(|t|^{2H}+ |s|^{2H}- |t-s|^{2H}),\]

where H is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. The value of H determines what kind of process the fBm is:

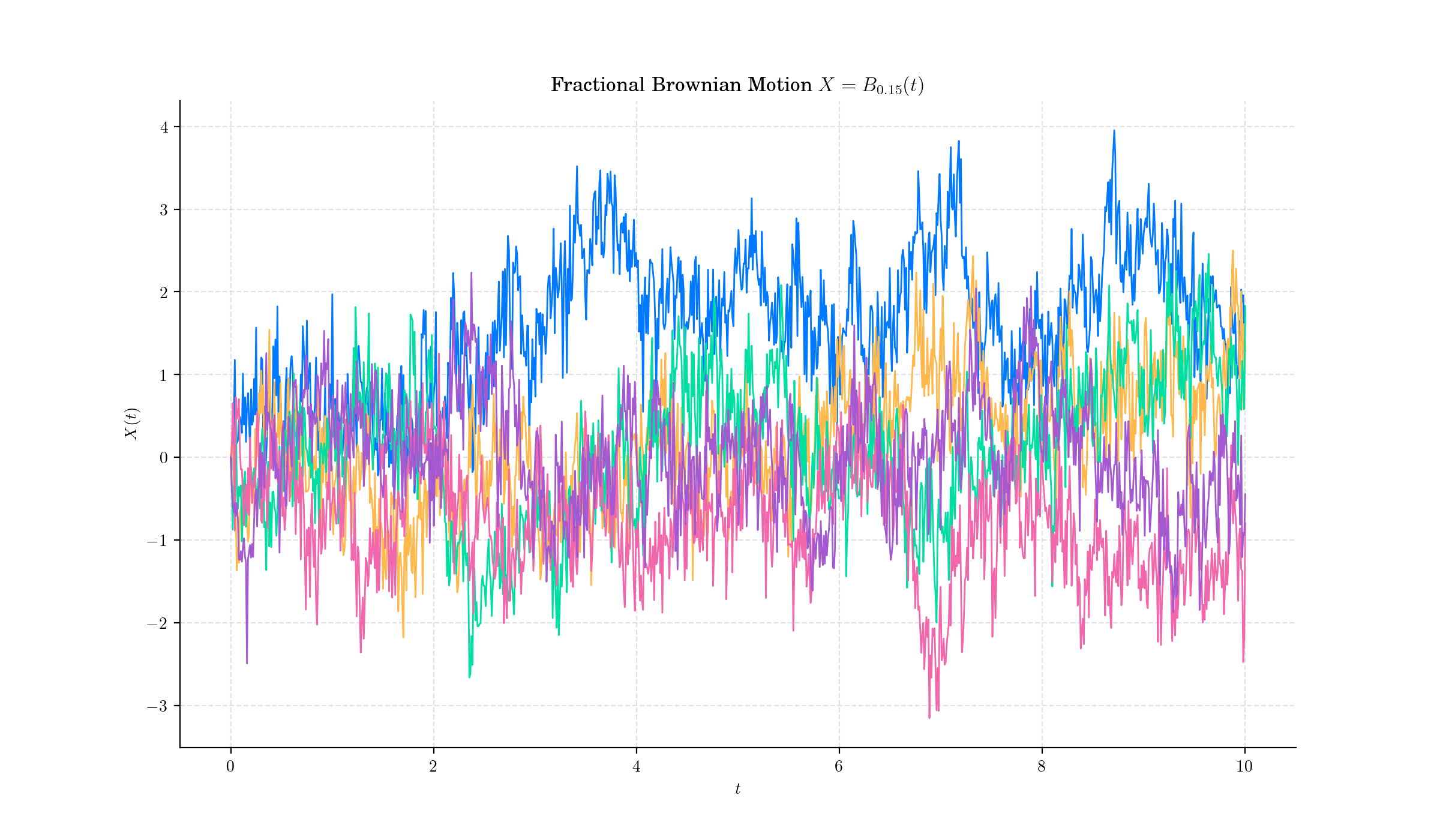
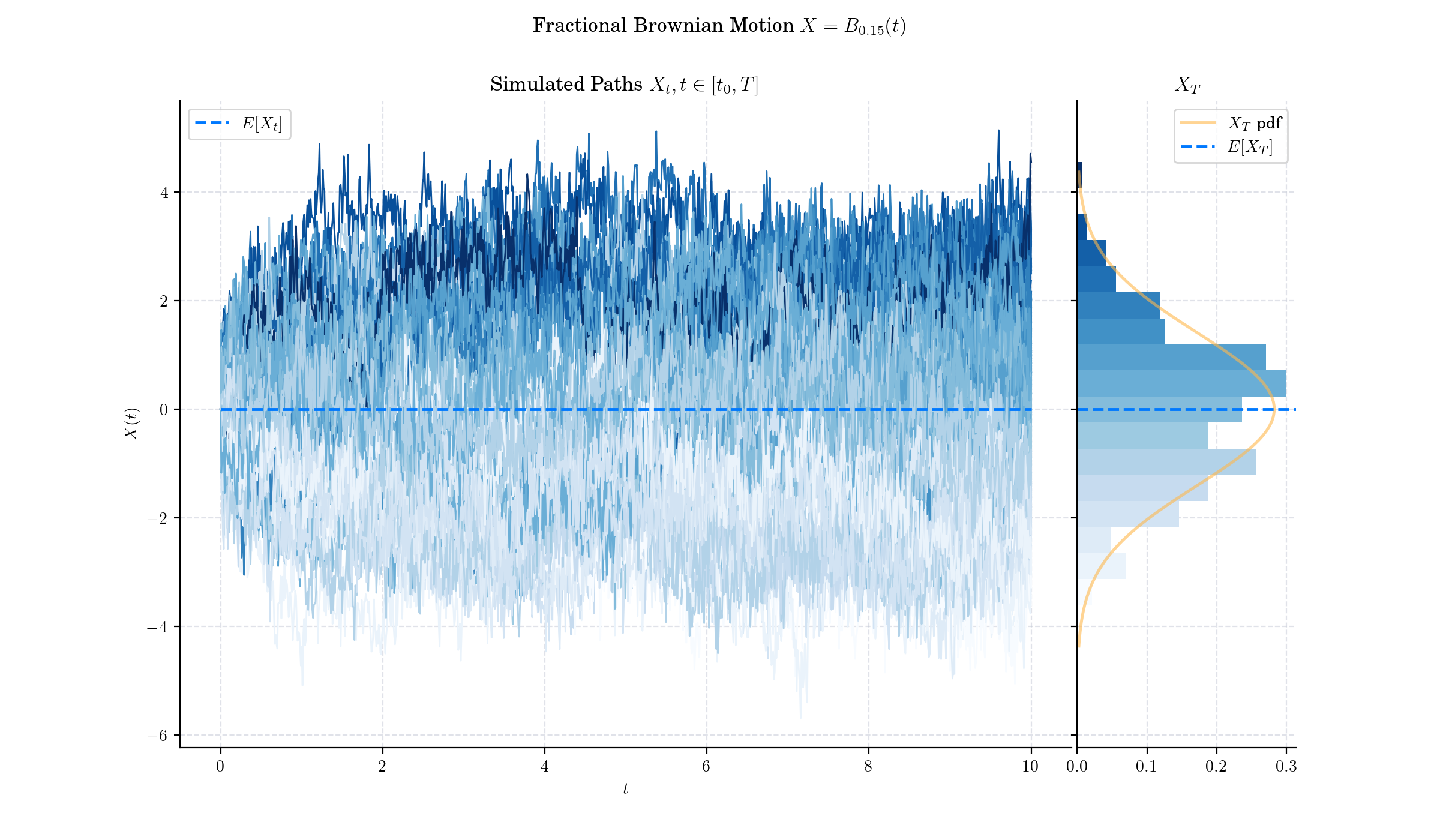
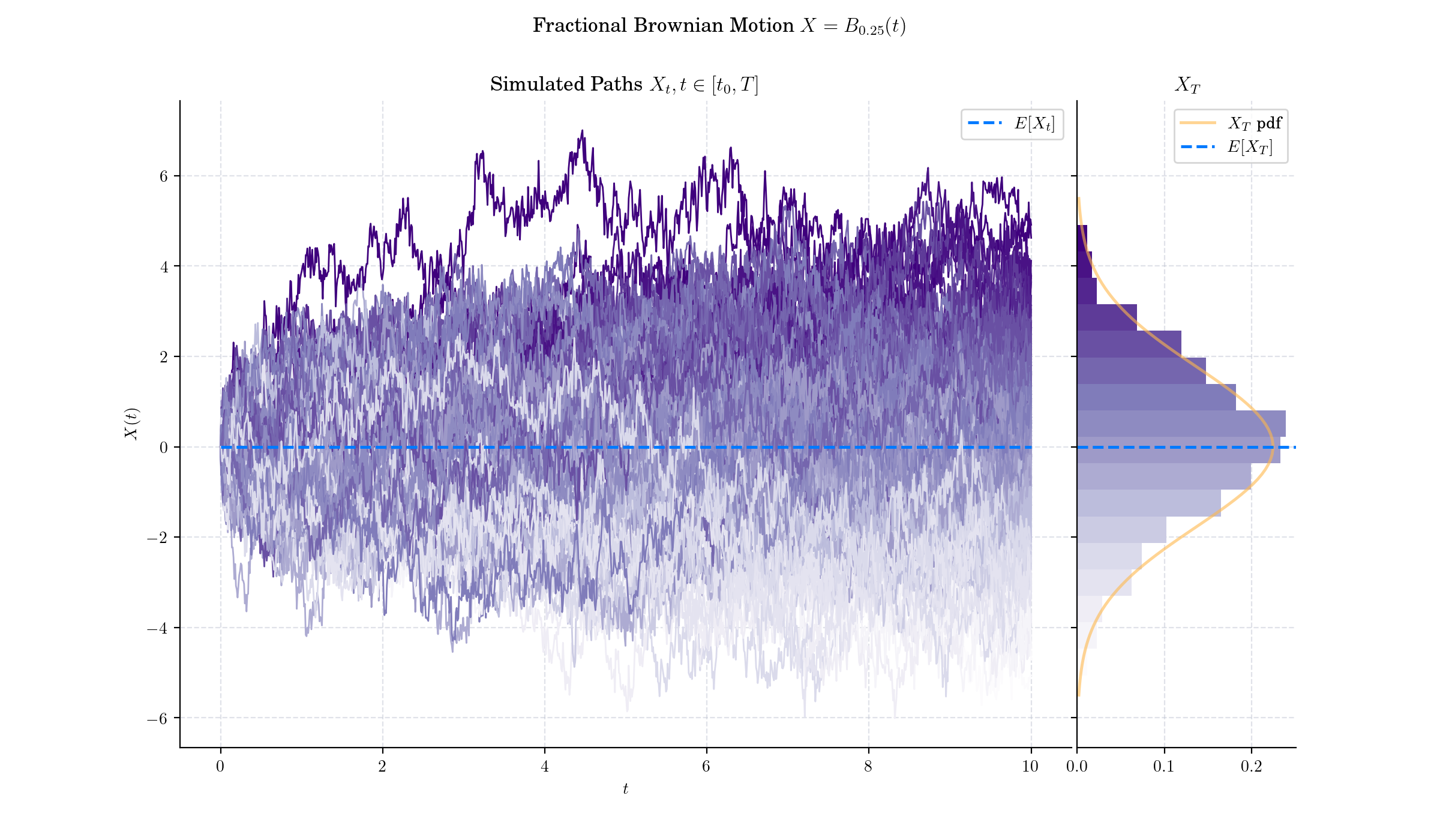
  • if H < 1/2 then the increments of the process are negatively correlated.

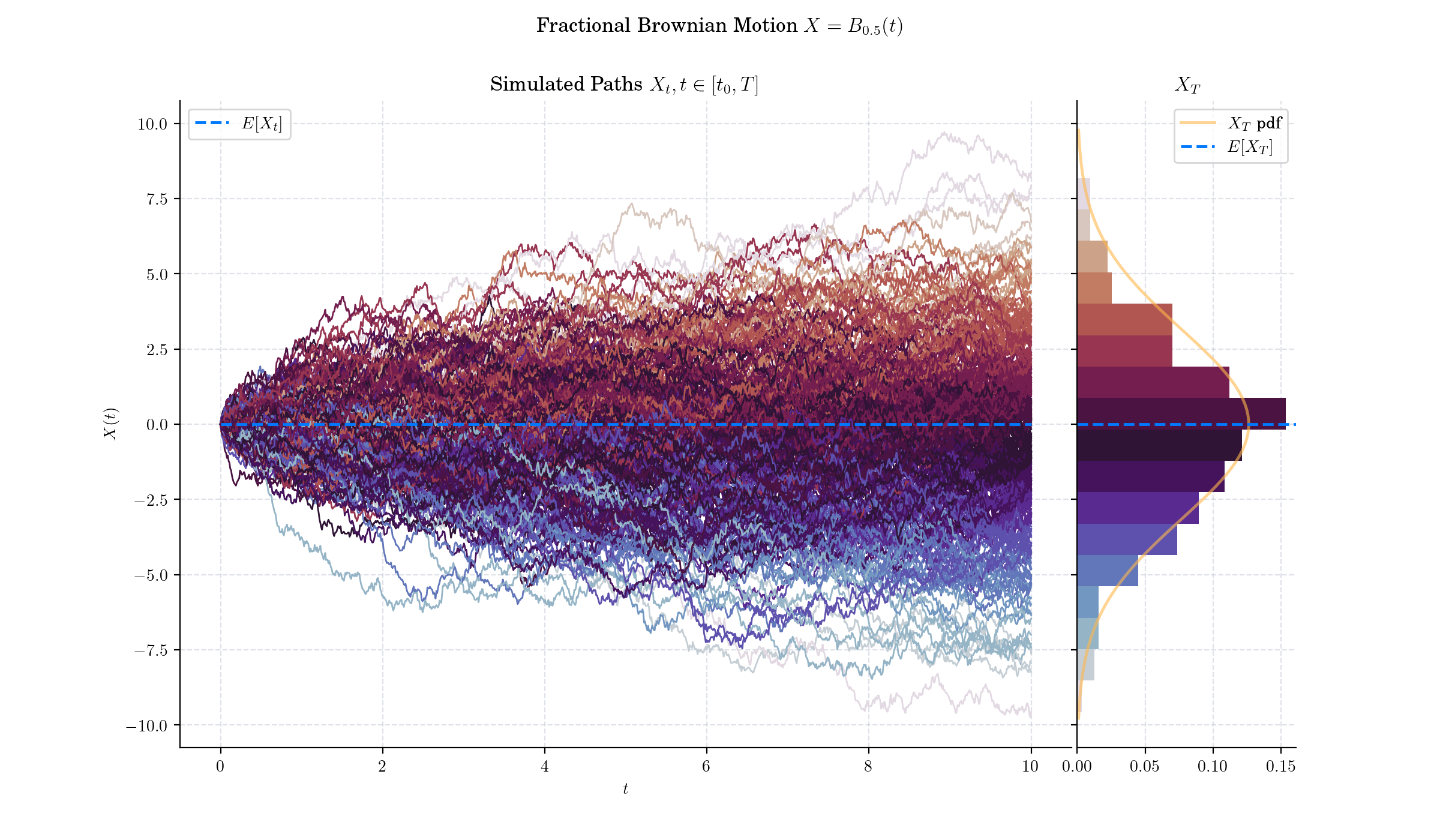
  • if H = 1/2 then the process is in fact a Brownian motion or Wiener process;

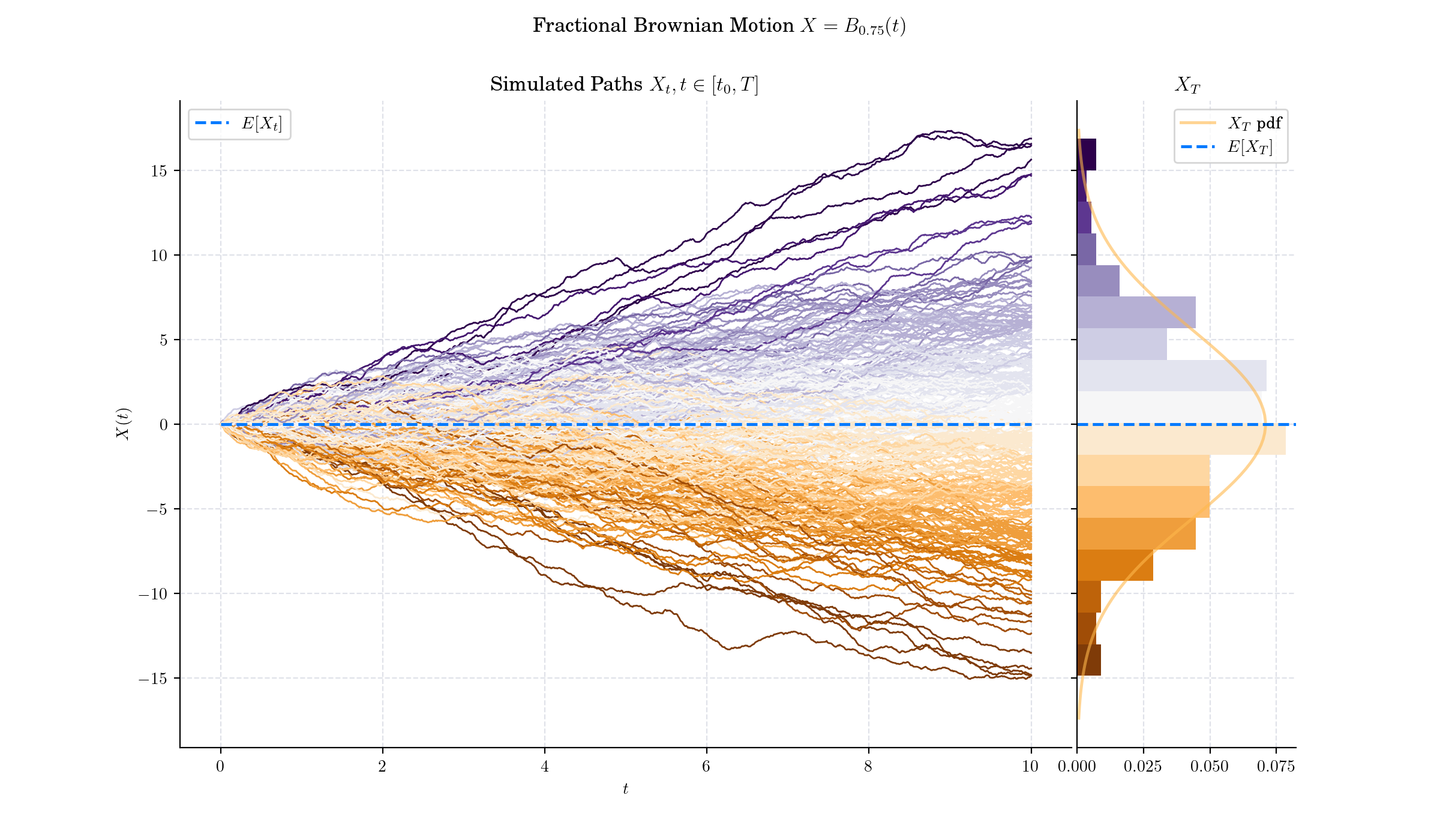
  • if H > 1/2 then the increments of the process are positively correlated;

đź”” Random Facts đź””#

  • Although the main principles of fBM were introduced earlier by Kolmogorov, the name was introduced by Mandelbrot and van Ness (1968) who defined the process as a stochastic integral

  • The Hurst exponent describes the raggedness of the resultant motion, with a higher value leading to a smoother motion. It was introduced by Mandelbrot & van Ness (1968).

  • There is a generalisation of fractional Brownian motion: n-th order fractional Brownian motion, abbreviated as n-fBm.  n-fBm is a Gaussian, self-similar, non-stationary process whose increments of order \(n\) are stationary.

  • The main difference between fractional Brownian motion and regular Brownian motion is that while the increments in Brownian Motion are independent, increments for fractional Brownian motion are not.

  • Various methods have been developed to generate samples of fBm efficiently. To produce our visualisations we use the Davies-Harte method which relies on the Fast Fourier Transform (FFT) and is computationally efficient with complexity \(O(n log(n))\).

More to Read đź“š#

  • Mandelbrot, Benoit B., and John W. Van Ness. “Fractional Brownian Motions, Fractional Noises and Applications.” SIAM Review, vol. 10, no. 4, 1968, pp. 422–37. JSTOR, http://www.jstor.org/stable/2027184.

  • Davies, R. B., and D. S. Harte. “Tests for Hurst Effect.” Biometrika, vol. 74, no. 1, 1987, pp. 95–101. JSTOR, https://doi.org/10.2307/2336024.

  • Sainty, P. (1992), “Construction of a complex-valued fractional Brownian motion of order N”, Journal of Mathematical Physics, 33 (9): 3128, Bibcode:1992JMP….33.3128S, doi:10.1063/1.529976

P.s. If you are curious about probability distributions visit the Advent Calendar 2023 ✨

Contents