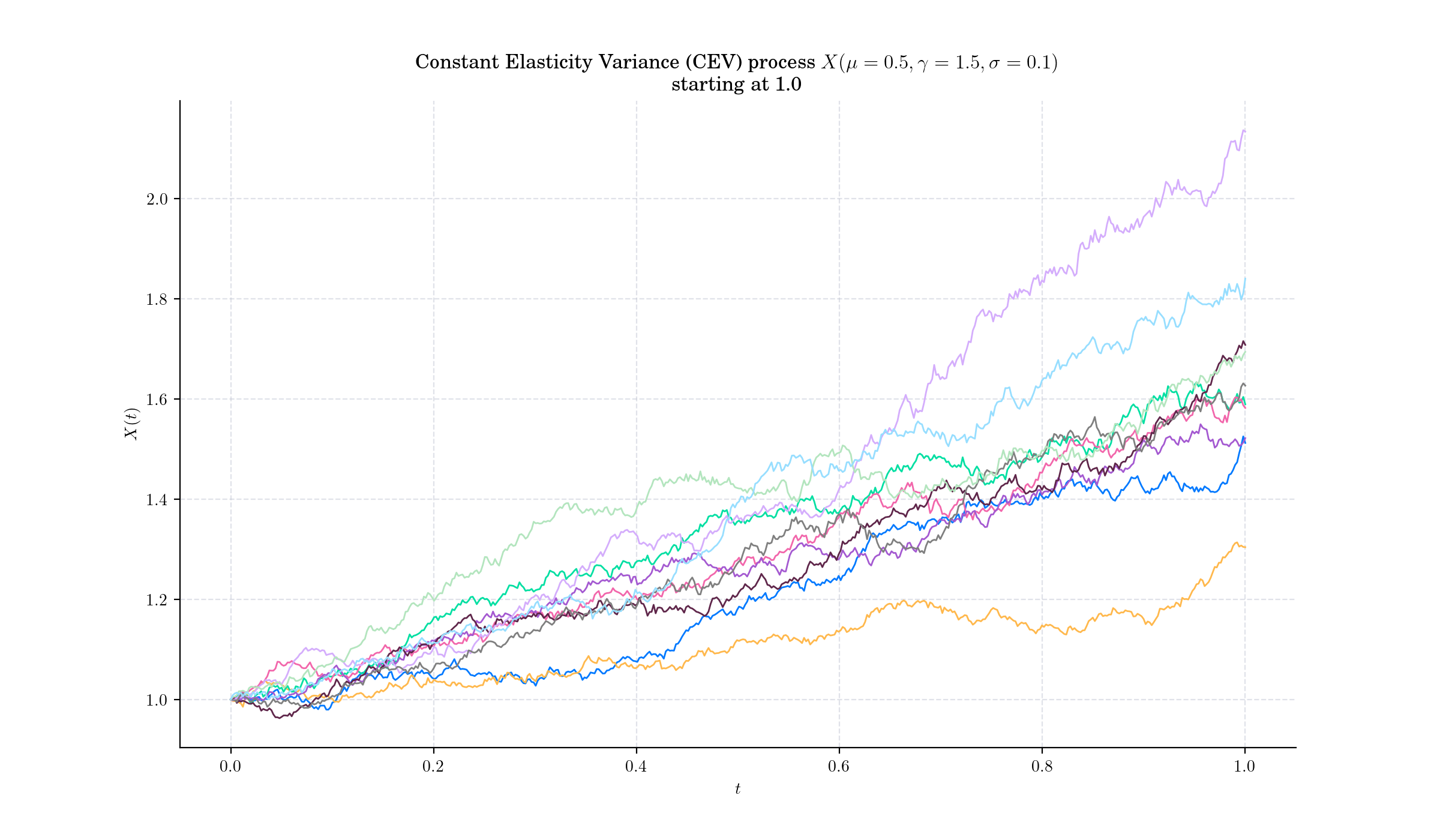
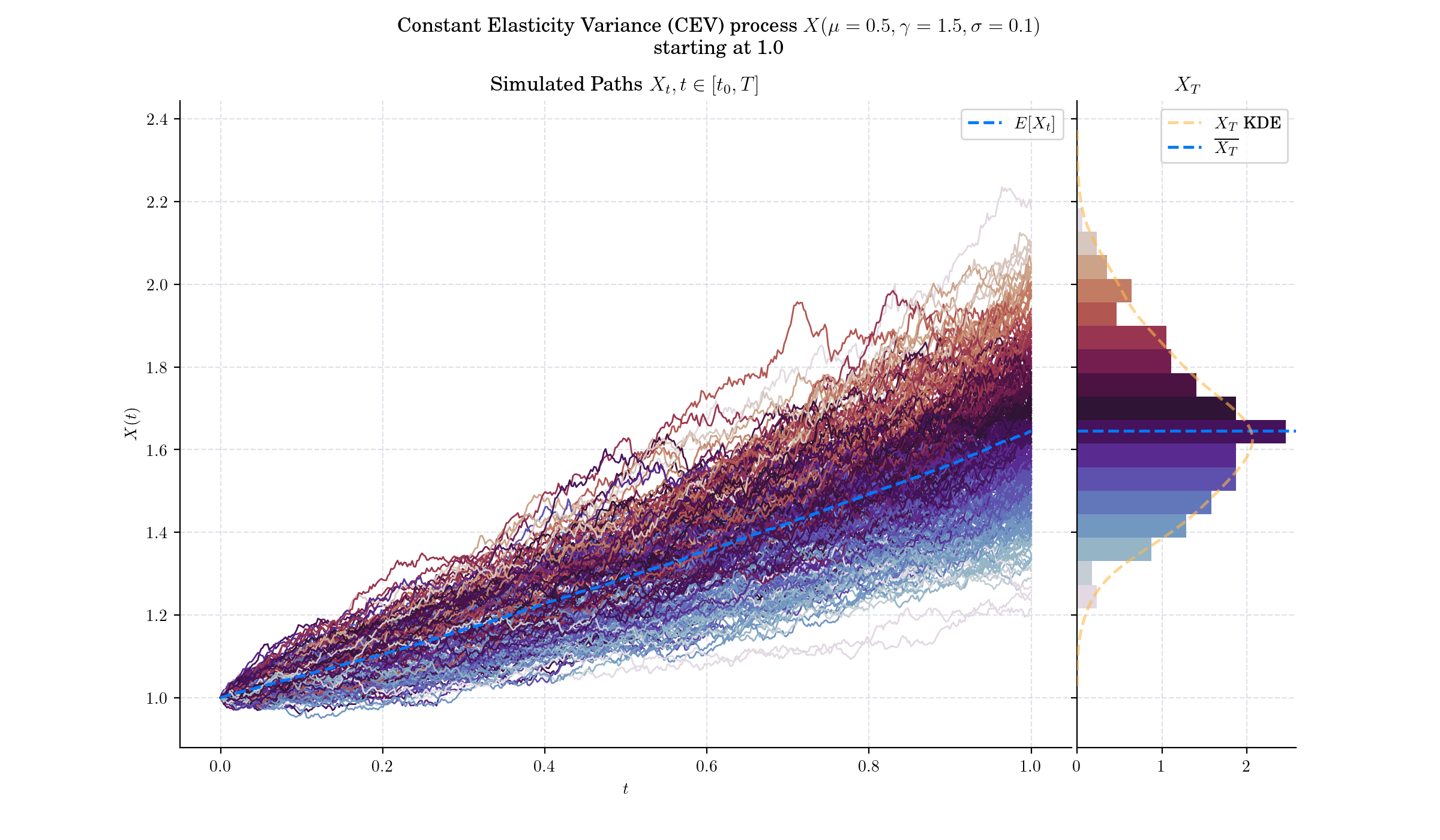
Day 17: CEV Process

In mathematical finance, the Constant Elasticity of Variance (CEV) model is a local volatility model, that attempts to capture stochastic volatility and the leverage effect. The model is widely used by practitioners in the financial industry, especially for modelling equities and commodities.

Definition

The Constant Elasticity of Variance (CEV) model describes a process following Stochastic Differential Equation (SDE)

\[dX\_t = \mu X\_t dt + \sigma X\_t^{\gamma} dW\_t, \quad t >0,\]

with initial condition \(X\_0 =x\_0\in\mathbb{R}\); where \(W\_t\) is a standard Brownian motion, and the three parameters are constants.

• \(\mu\) is the drift parameter

• \(\sigma\) is the constant volatility coefficient

• \(\gamma\) is the elasticity parameter

• 

🔔 Random Facts 🔔

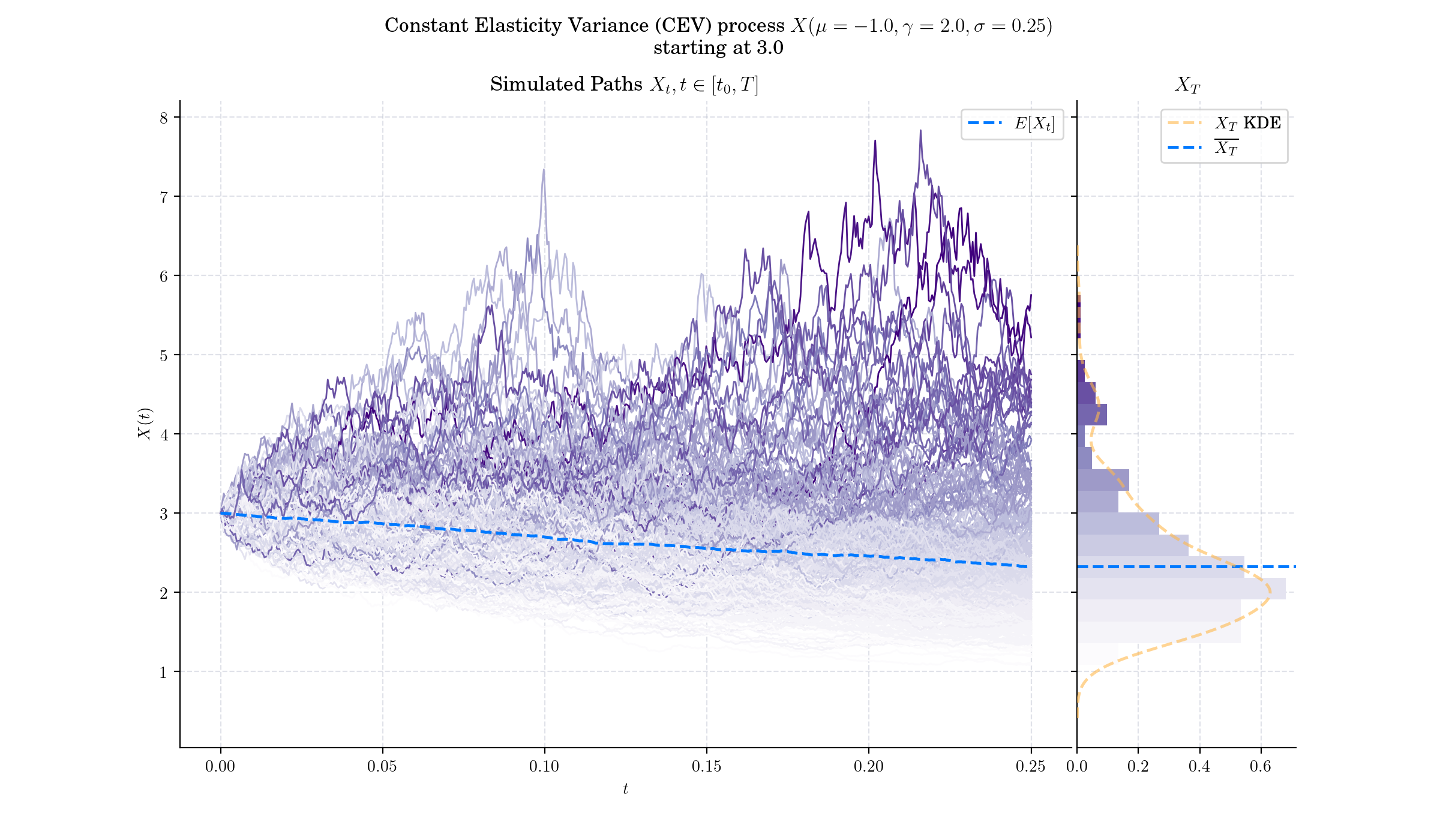
• The CEV model was first introduced by economist John Cox in 1975 in his seminal paper “Notes on Option Pricing I: Constant Elasticity of Variance Diffusions.” Cox proposed the model as a more realistic alternative to the Black-Scholes framework to better capture the behaviour of financial markets, especially the relationship between volatility and asset price levels.

• The key feature of the CEV model lies in the difussion coefficient \(\sigma X\_t^{\gamma}\), which scales the volatility of the asset.

  • When \(\gamma=1,\) the process in the CEV model corresponds to a Geometric Brownian motion, which means that the model reduces to the the Black-Scholes model

  • For \(\gamma<1,\) the volatility decreases as the asset price increases –this is commonly observed in the Equities markets

  • For \(\gamma>1,\) the volatility increases with the asset price –observed in the Commodity markets

• Since its introduction, the CEV model has been widely studied and extended. It remains a cornerstone in the field of stochastic processes and financial modeling, particularly for its ability to explain phenomena observed in real-world markets.

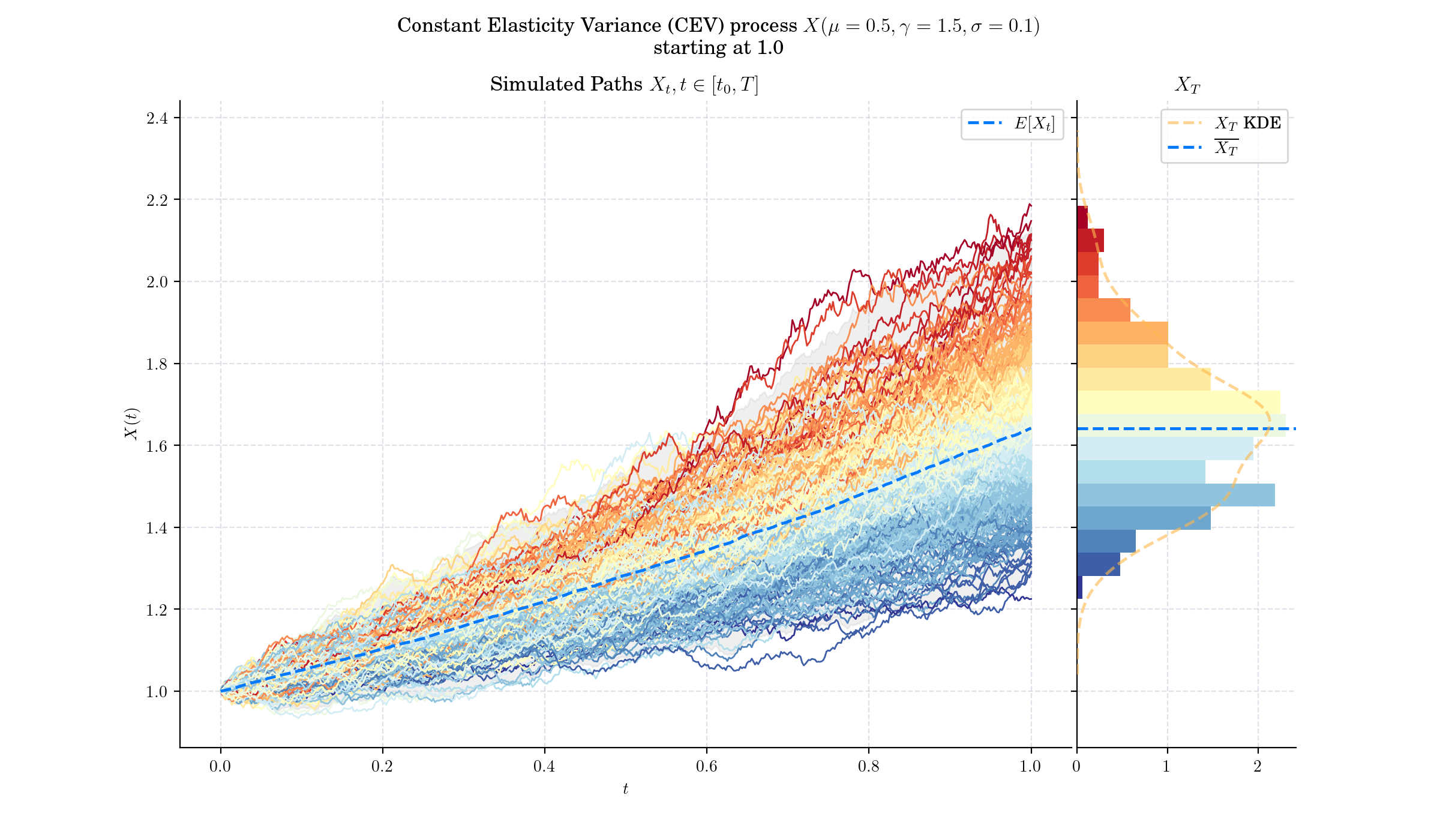
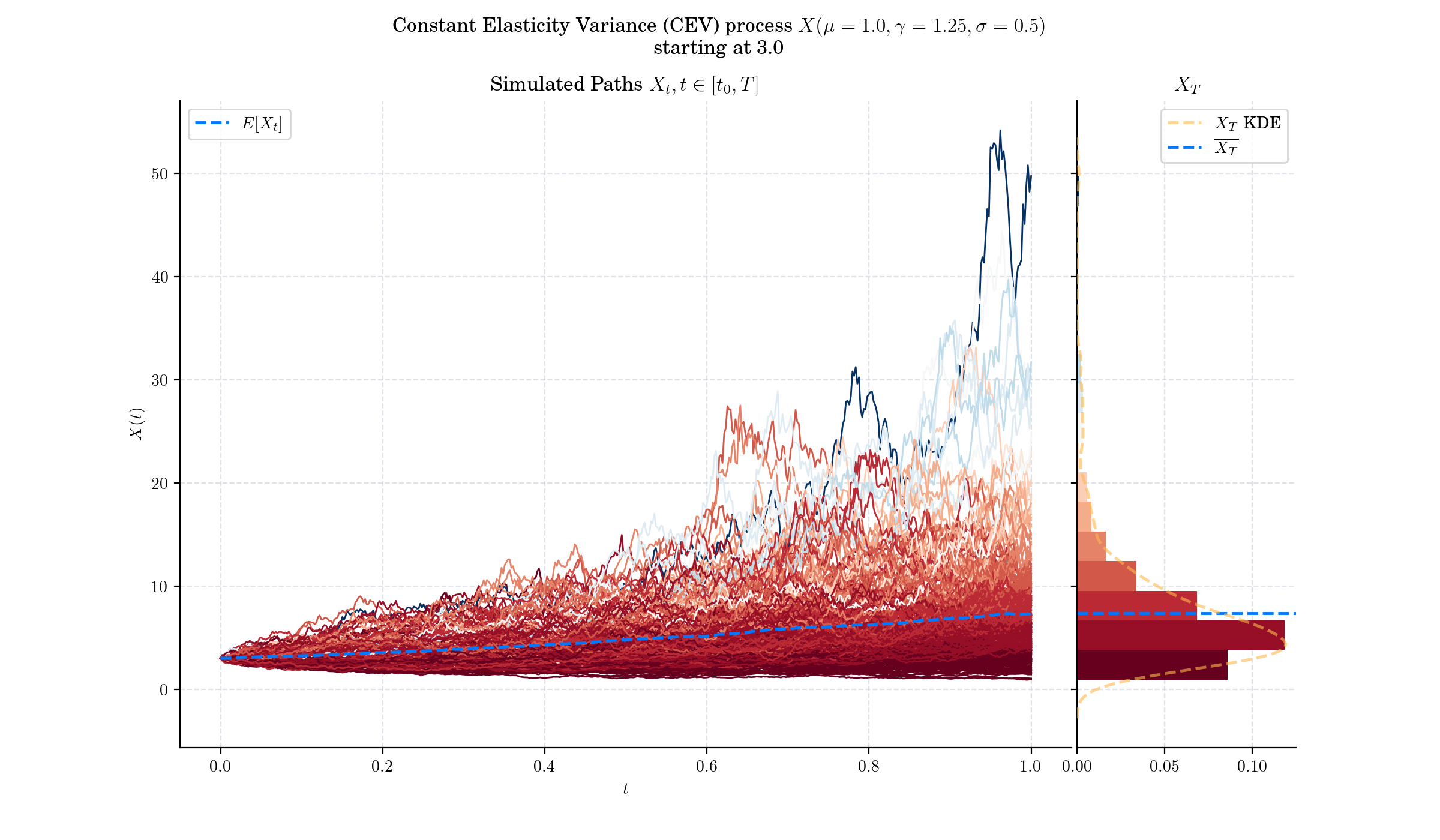
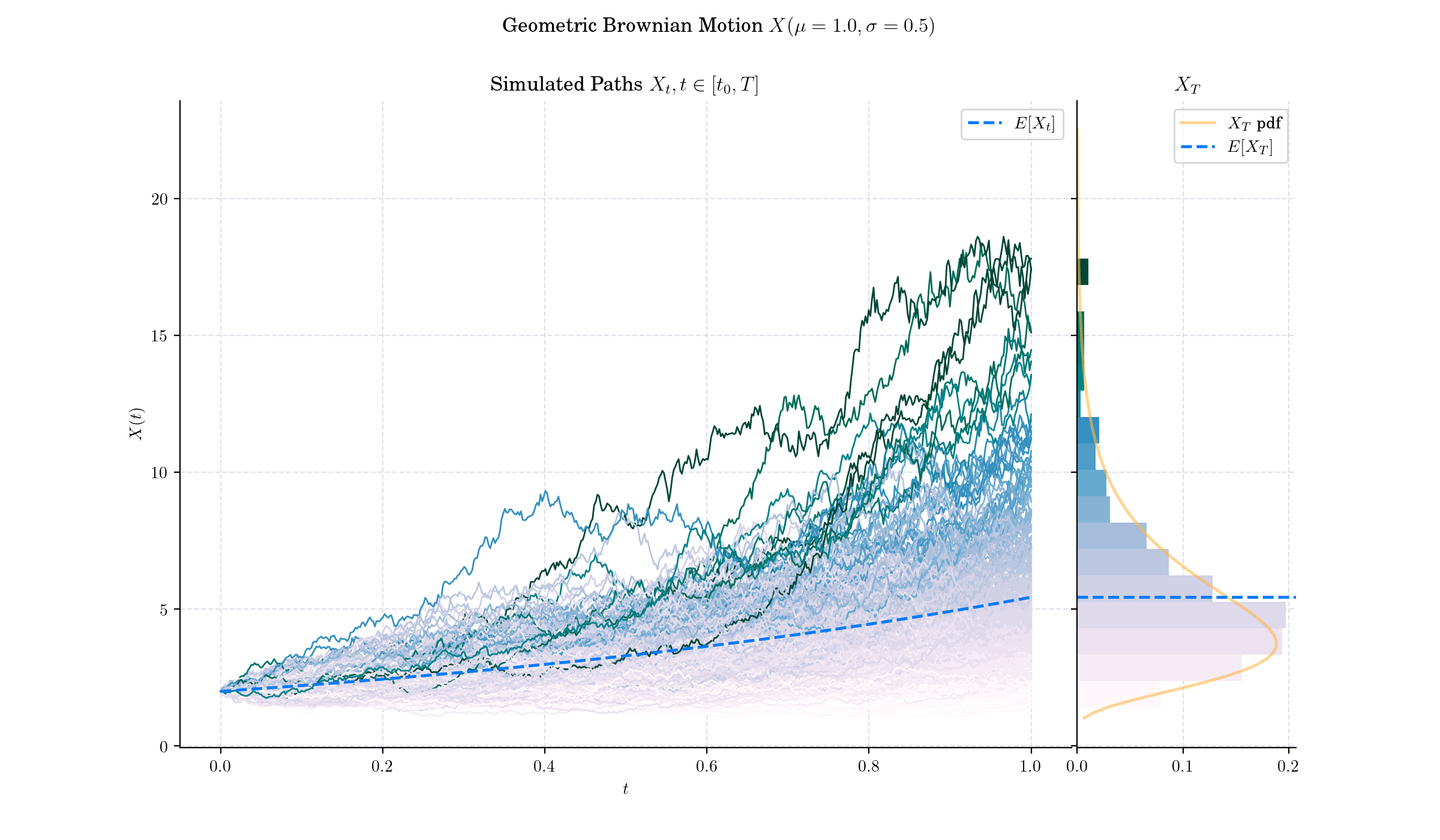
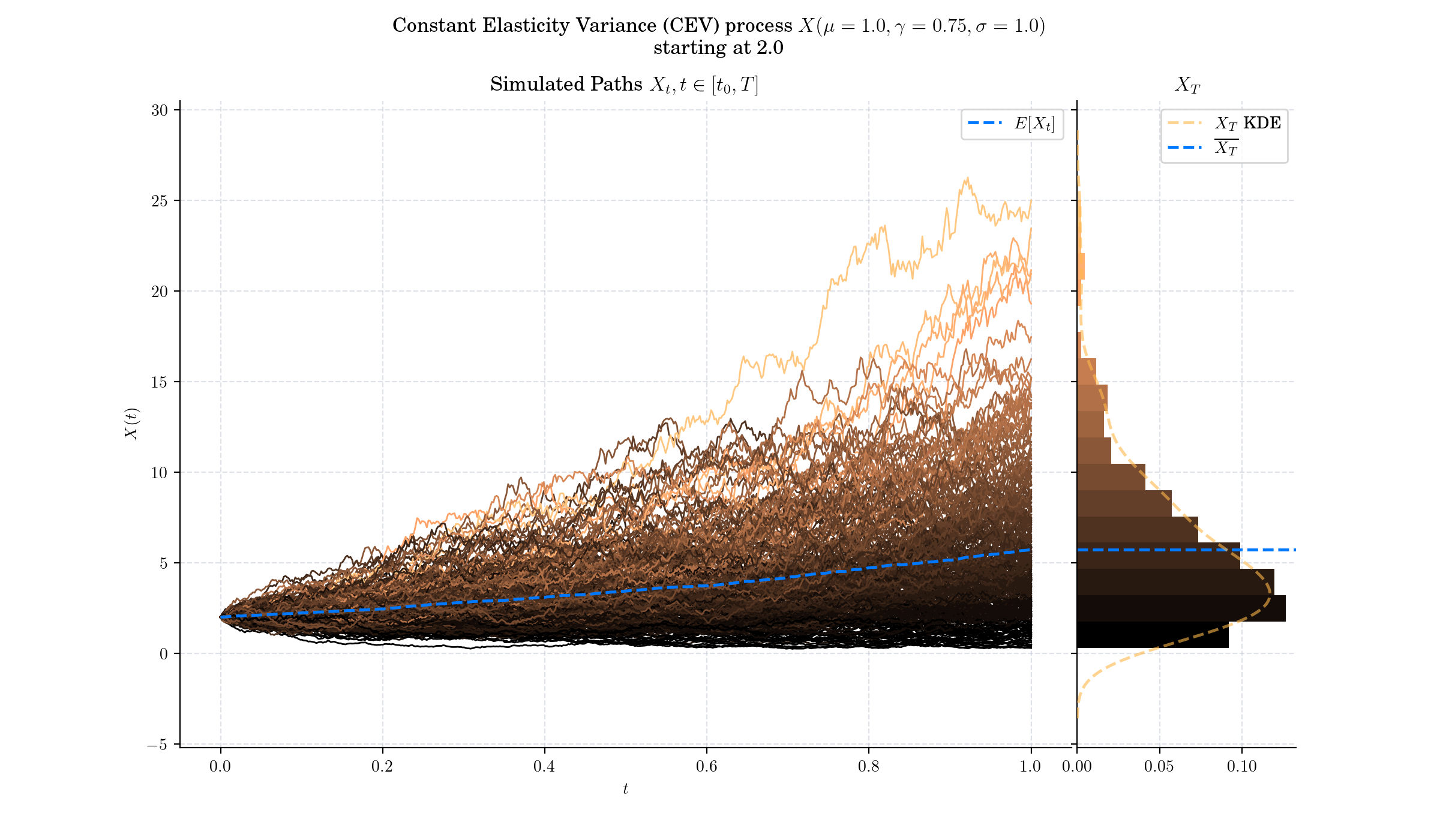
More to Read 📚

• Cox, J. “Notes on Option Pricing I: Constant Elasticity of Diffusions.” Unpublished draft, Stanford University, 1975.

• Yuen, K. C., et al. “ESTIMATION IN THE CONSTANT ELASTICITY OF VARIANCE MODEL.” British Actuarial Journal, vol. 7, no. 2, 2001, pp. 275–92. JSTOR, http://www.jstor.org/stable/41141790. Accessed 17 Dec. 2024.

• Lindsay, Alan and Brecher, Dominic, Results on the CEV Process, Past and Present (March 9, 2010). Available at SSRN: https://ssrn.com/abstract=1567864 or http://dx.doi.org/10.2139/ssrn.1567864

• Y.L. Hsu, T.I. Lin, C.F. Lee, Constant elasticity of variance (CEV) option pricing model: Integration and detailed derivation, Mathematics and Computers in Simulation, Volume 79, Issue 1, 2008, Pages 60-71, ISSN 0378-4754, https://doi.org/10.1016/j.matcom.2007.09.012.

P.s. If you are curious about probability distributions visit the Advent Calendar 2023 ✨