Day 4 : Pareto

The Pareto distribution, named after the Italian polymath Vilfredo Pareto, is a probability distribution that is used to describe many types of observable phenomena (e.g. in social and actuarial sciences, quality control, and economics ); the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto distribution is defined by a a shape parameter (also called a slope parameter or Pareto index) \(\alpha>0\), and a scale parameter \(x_m>0\).

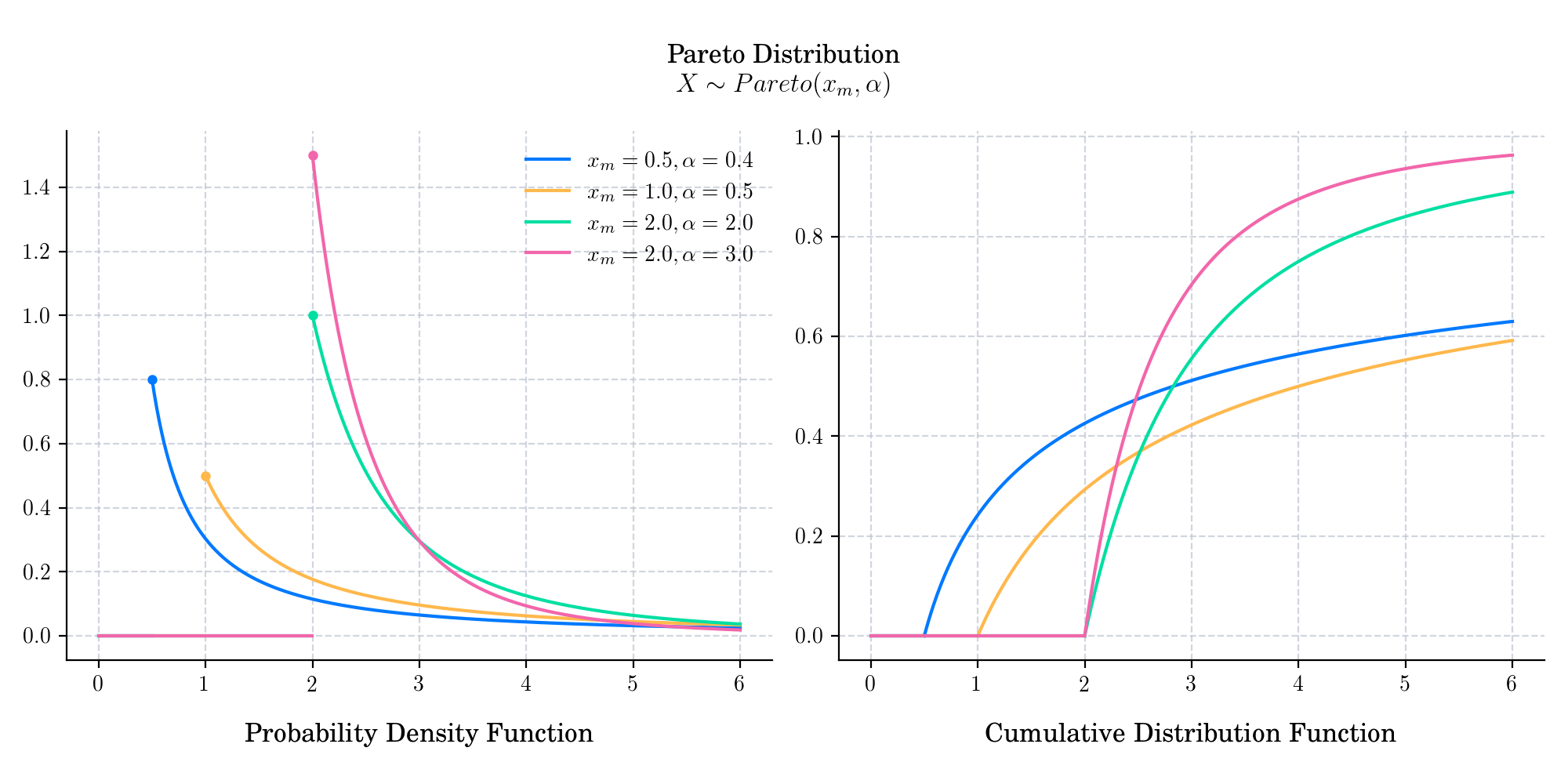
The probability density function is given by

\[f(x) = \frac{\alpha x_m^{\alpha}}{x^{\alpha + 1}} 1_{[x_m, \infty)}(x).\]

The cumulative distribution function is given by

\[F(x) = \left[ 1 - \left(\frac{ x_m}{x}\right)^{\alpha} \right] 1_{[x_m, \infty)}(x).\]

🔔 Random Facts 🔔

• Let \(X\) be a random variable which follows a Pareto distribution \(X\sim Pareto(x_m, \alpha)\), and \(x_1> x_m\). The conditional distribution of \(X\) given \(X\geq x_1\), is also Pareto with the same Pareto index \(\alpha\) and scale parameter \(x_1\). This property means that the Pareto distribution is closed with respect to conditioning on a right-tail event.

• The moment generating function of the Pareto distribution does not exist.