Day 11 : F

The F-distribution is also known as F-ratio, Snedecor’s F distribution, or the Fisher–Snedecor distribution after British polymath Ronald Fisher and American mathematician George W. Snedecor. It is a continuous probability distribution with support on \([0, \infty)\), defined by two parameters \(d_1, d_2 >0\) which are called degrees of freedom. More precisely, the \(F\) distribution with \(d_1\) and \(d_2\), degrees of freedom is the distribution given by \(X = \frac{S_1/ d_1}{ S_2/d_2}\) where \(S_1\) and \(S_2\) are independent random variables with chi-square distributions with respective degrees of freedom \(d_1\) and \(d_2\).

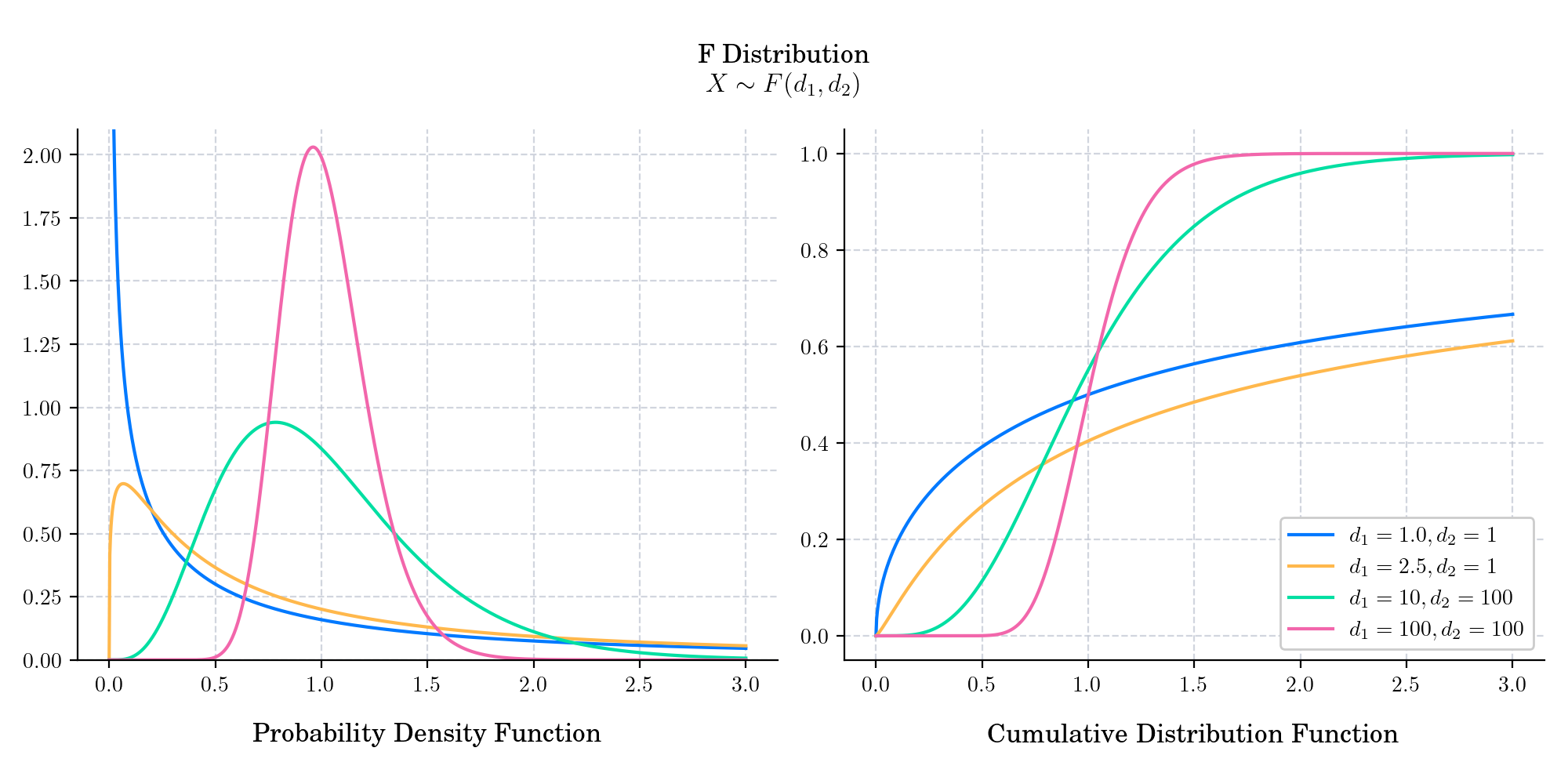
The probability density function is given by

\[f(x) = \frac{1}{x B\left(\frac{d_1}{2}, \frac{d_2}{2} \right)} \sqrt{ \frac{ (d_1x)^{d1} d_2^{d2} }{ (d_1x + d_2)^{d_1 + d_2} } }\]

where \(B\) is the beta function.

The cumulative distribution function is given by

\[F(x) = I_{d_1x/(d_1x + d_2)}\left( \frac{d_1}{2}, \frac{d_2}{2} \right)\]

where \(I\) is the regularized incomplete beta function.

🔔 Random Facts 🔔

• It arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA)

• If \(X \sim F(d_1, d_2)\), then \(X^{-1} \sim F(d_2, d_1)\).

• Its moment generating function does not exist

• There is no analytical expression for the characteristic function of the F distribution. But it can be written in terms of the confluent hypergeometric function of the second kind. This was shown by British econometrician P.C.B Phillips in his paper The True Characteristic Function of the F Distribution (1982, Biometrika)