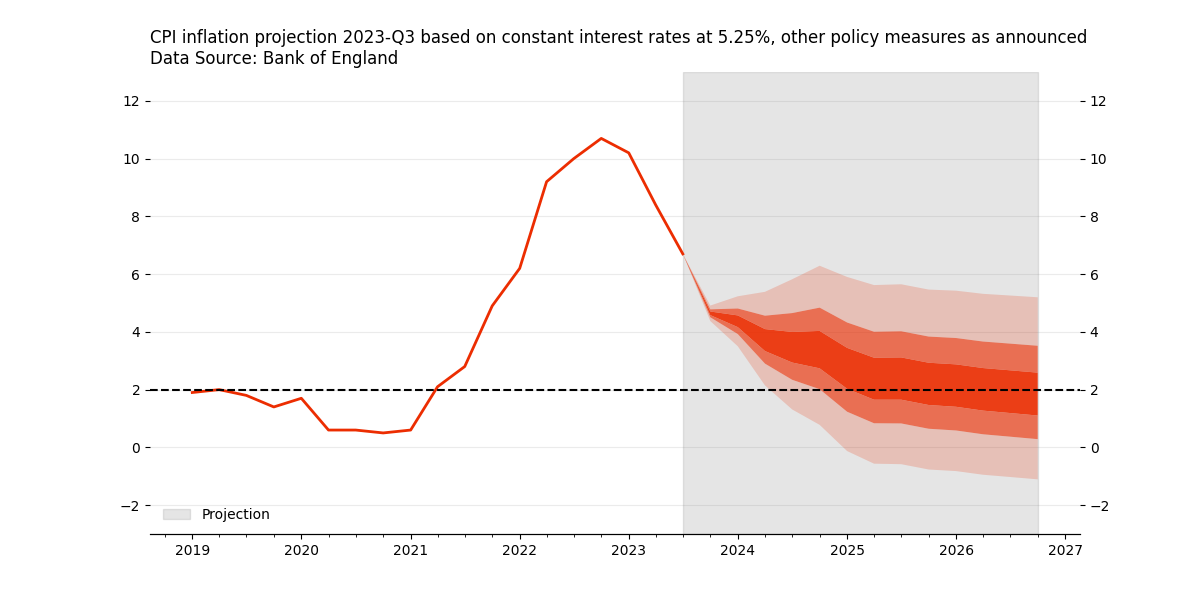
Day 23 : Two-Piece Normal Distribution

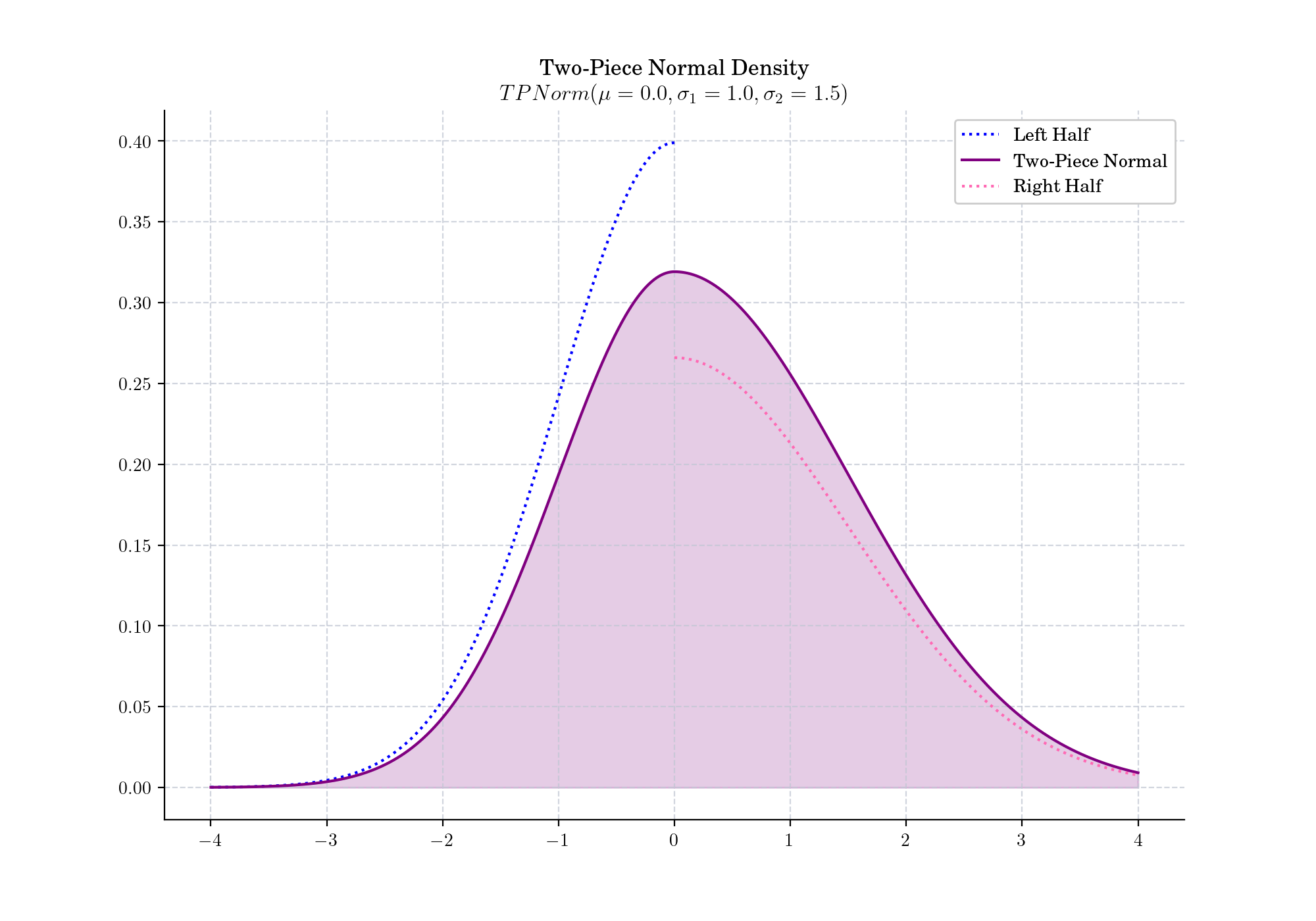
The two-piece normal, also known as split normal, binormal, or double-Gaussian, results from joining at the mode the corresponding halves of two normal distributions with the same mode \(\mu\) but different standard deviations \(\sigma_1\) and \(\sigma_2\). This idea can be seen in the following plot where we can see the two half densities (in blue and pink) and the resulting two-piece normal density (in purple).

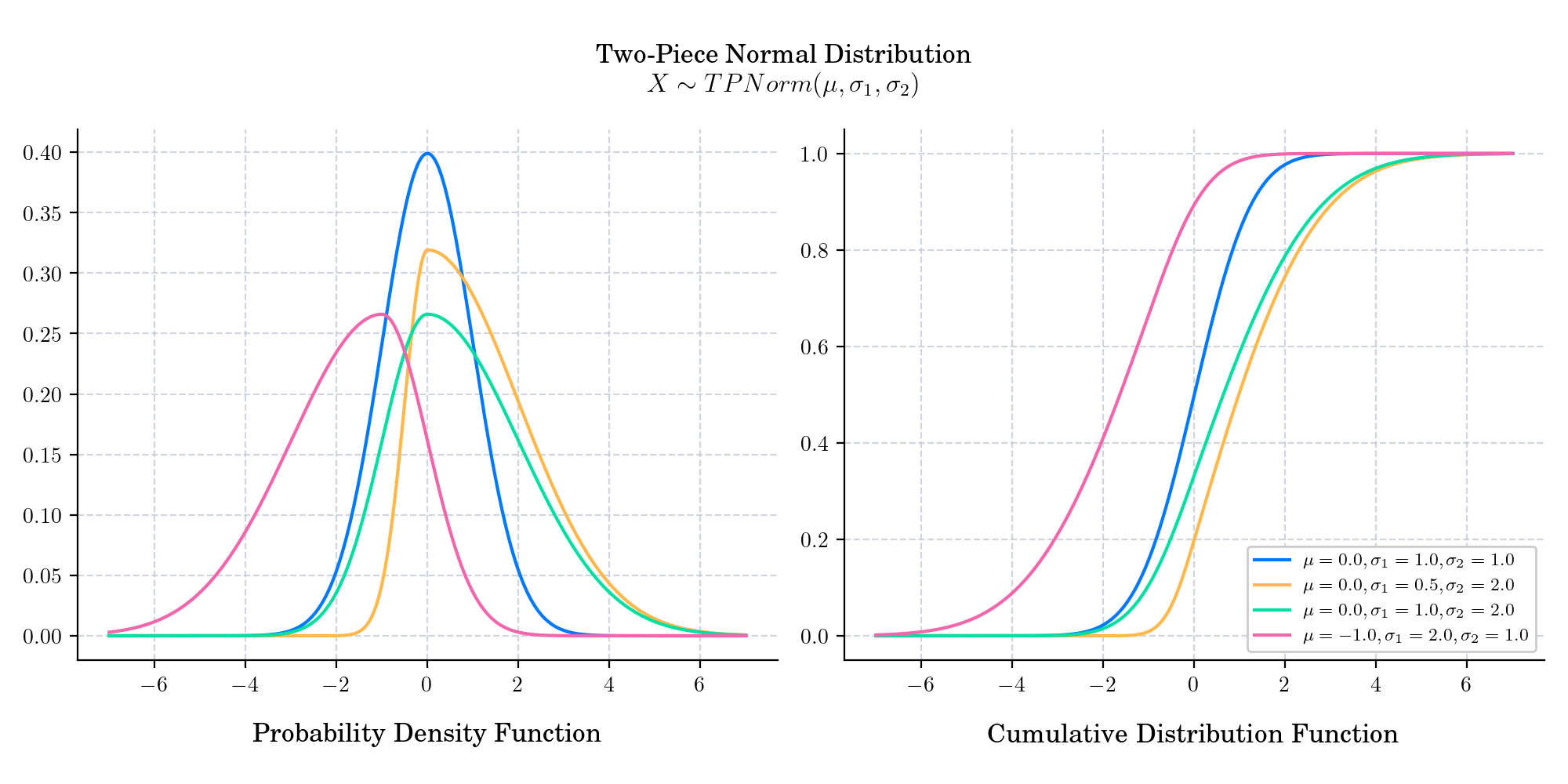
The probability density function is given by

\[\begin{split} f(x) = \begin{cases} \dfrac{2}{\sigma_1+\sigma_2}\phi\left(\dfrac{x-\mu}{\sigma_1}\right), \qquad \mbox{if } x < \mu, \\ \dfrac{2}{\sigma_1+\sigma_2}\phi\left(\dfrac{x-\mu}{\sigma_2}\right), \qquad \mbox{if } x \geq \mu. \\ \end{cases} \end{split}\]

where \(\phi\) denotes the density function of a standard normal distribution.

🔔 Random Facts 🔔

• The two-piece normal was proposed by German physicist and phycologist Gustav Fechner -who is also consider the founder of psychophysics- around 1887 but published posthumously ten years later. Unfortunately, Fechner work did not become popular and this lead to a series of re discoveries (as recent as 2016!).

• If \(\sigma_1=\sigma_2\), then the two-piece normal becomes a normal distribution.

• The Two-Piece normal, and more generally the family of two-piece distributions, have been extensively used in applications such as:

  • Bank of England Fan Charts for Inflation Report

  • Measurement Errors Models

  • Forecasting and Estimation of Risk

Today’s bonus plot is a fan chart showing the historical CPI inflation as well as its projection as of 2023-Q3. The Bank of England uses a two-piece normal distribution to model the quarterly inflation forecasts.