Day 6 : Arcsin

The standard arcsine (or simply arcsine) distribution is a special case of the beta distribution (see Day 2 of the Calendar) with α = β = 1/2.

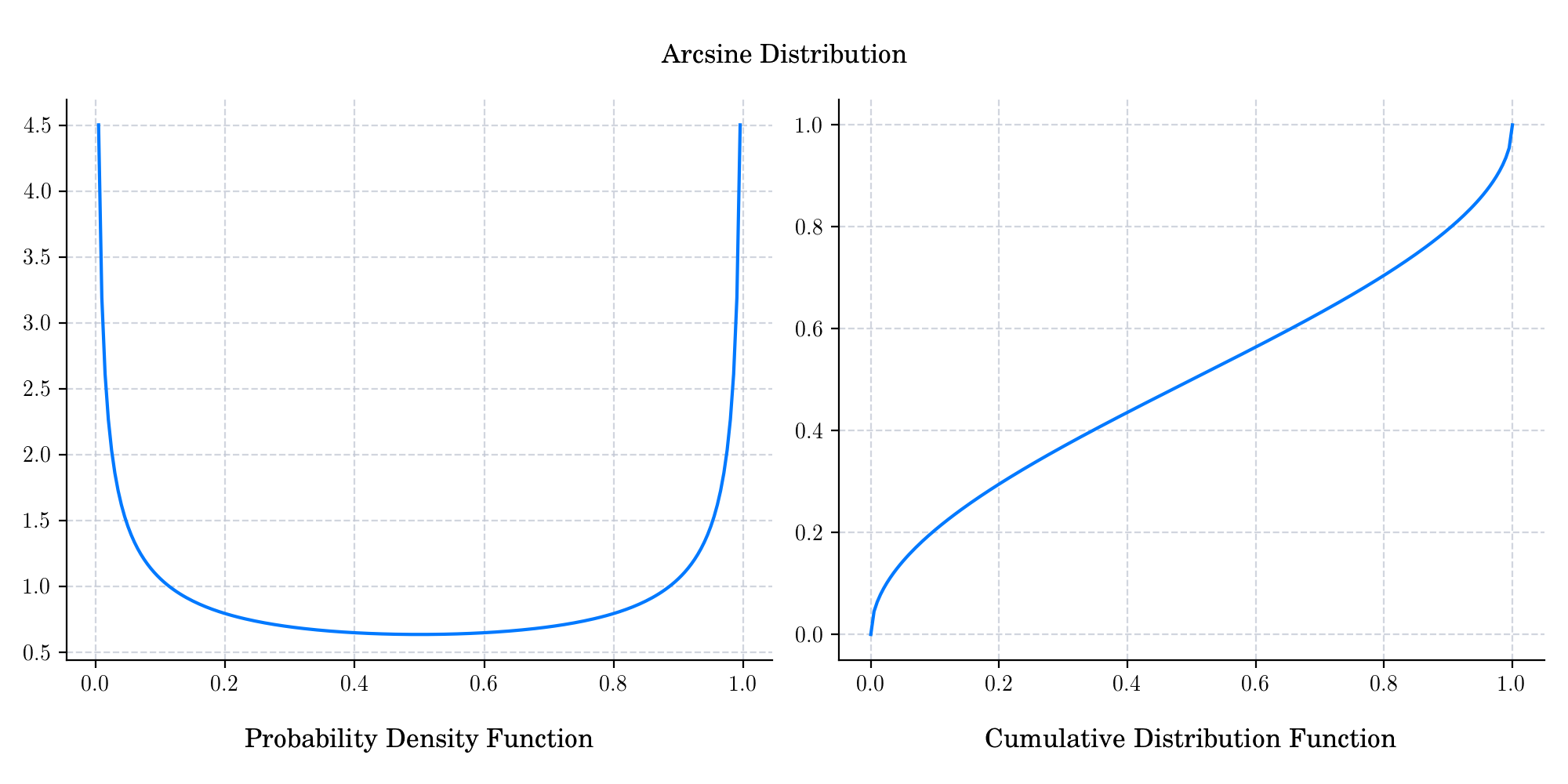
The probability density function is given by

\[f(x) = \frac{1}{\pi \sqrt{x(1-x)}}, \qquad x\in [0,1].\]

The cumulative distribution function is given by

\[F(x) = \frac{2}{\pi} \arcsin (\sqrt{x}), \qquad x\in [0,1].\]

🔔 Random Facts 🔔

• Let \(\{W(t) : t\in[0,1] \}\) be a standard Brownian motion on \([0,1]\), and consider the following random variables:

• The proportion of the time that \(W\) remains positive:

\[T^{+} = \lambda(\{ t\in[0,1] : W(t) >0\}),\]

where \(\lambda\) denotes the Lebesgue measure.

• The last time that \(W\) crosses the origin:

\[L = \sup \{ t \in [0,1] : W(t) = 0\}.\]

• The time at which \(W\) reaches its maximum:

\[M^{\ast} = \arg \max_{0\leq t\leq 1} W(t).\]

• These three random variables follow the arcsin distribution. These properties are known as arcsin laws (or Levy arcsine laws). In particular, the fact that \(L\sim Arcsin\), was noted by French mathematician Paul Lévy in 1939, in his paper “On certain homogeneous stochastic processes”.

• The prime divisors of natural numbers follow a distribution which is closely related to the Arcsine distribution. This was stated without proof in 1969 by Hungarian mathematician Paul Erdős, and subsequently proved (see e.g. Manstavičius, E. (1994), “A proof of the Erdős arcsine law”) and is now known as the Erdős arcsine law.