Day 13 : Exponential

The exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It has support \([0, \infty)\) and is defined by a parameter \(\lambda>0\) which is called rate (or inverse scale).

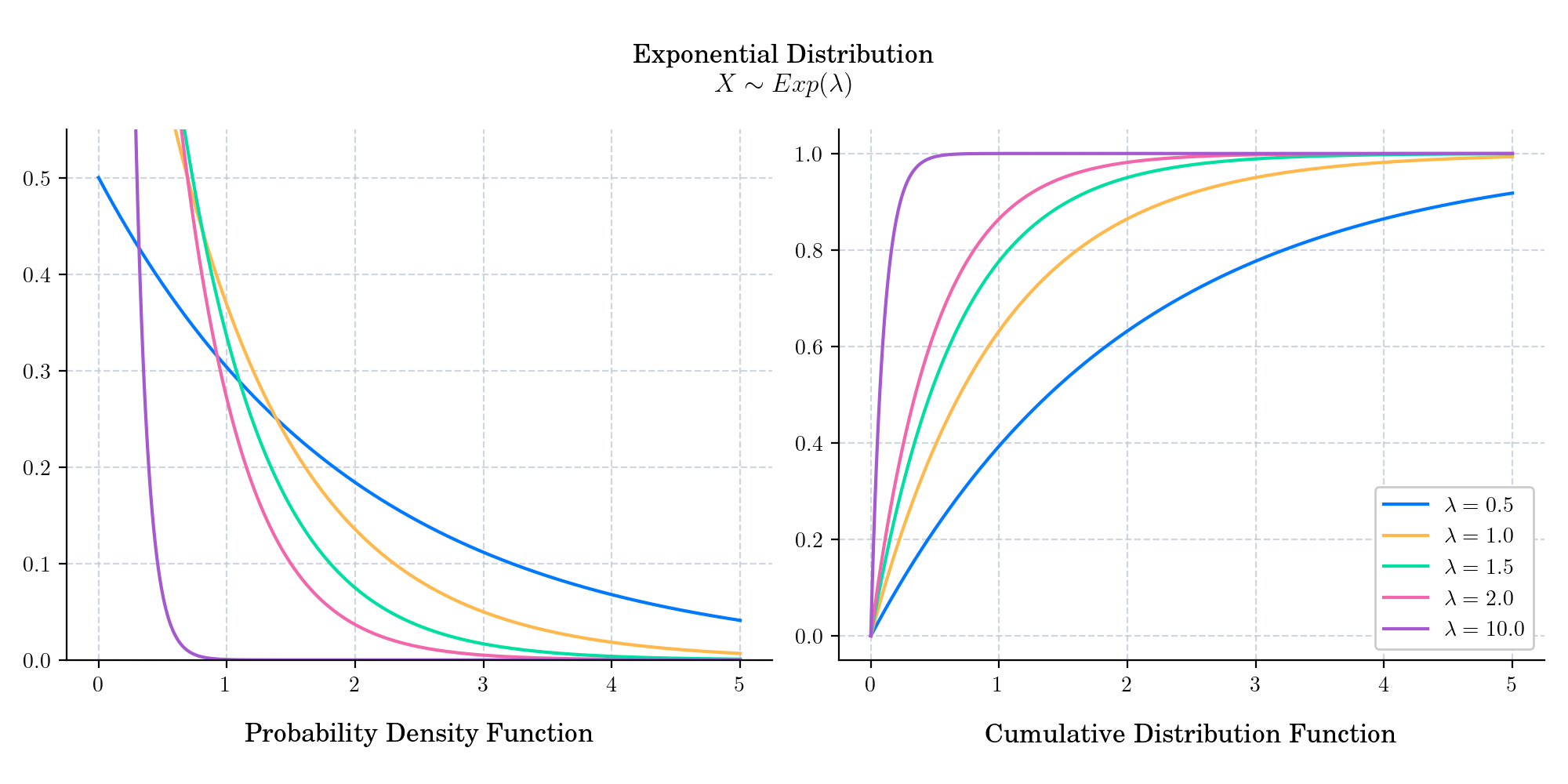
The probability density function is given by

\[f(x) = \lambda e^{-\lambda x}, \qquad x\geq 0.\]

The cumulative distribution function is given by

\[F(x) = 1 - e^{-\lambda x}, \qquad x\geq 0.\]

🔔 Random Facts 🔔

• An exponentially distributed random variable \(T\sim Exp(\lambda)\) obeys the relation \(P(T>s+t| T>s) = P(T>t)\). This property is known as memorylessness.

• The exponential distribution and the geometric distribution are the only memoryless probability distributions. The exponential distribution is consequently also necessarily the only continuous probability distribution that has a constant failure rate.

• If X ~ Pareto(1, λ), then log(X) ~ Exp(λ).

• In physics it is often used to measure radioactive decay, in engineering it is used to measure the time associated with receiving a defective part on an assembly line, and in finance it is often used to measure the likelihood of the next default for a portfolio of financial assets. It can also be used to measure the likelihood of incurring a specified number of defaults within a specified time period.