Day 21 : Zero-One Inflated Beta Distribution

In many instances real life data shows exact 0’s and 1’s occurring in additional to values between 0 and 1. Though the beta distribution covers a variety of the distribution shape, it does not accommodate excessive values at 0 and 1. The Zero-One Beta extends the Beta distribution to a piecewise distribution that accounts for probability mass at 0 and 1, in addition to the probability density within (0, 1). It is defined by four parameters \(0<\alpha, \gamma, \mu<1\), and \(\phi>0\).

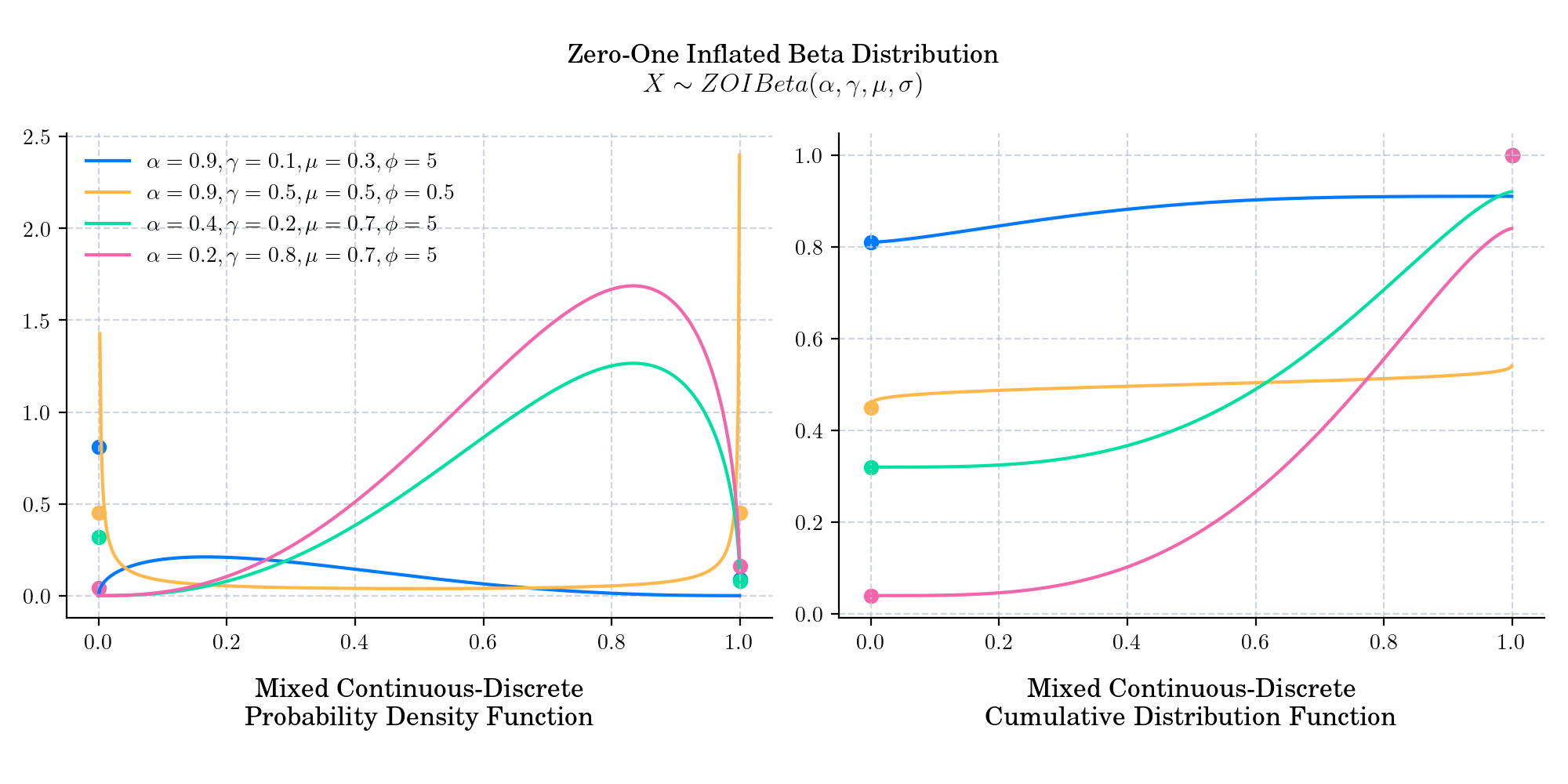
The probability density function is given by

\[\begin{split}f(x) = \begin{cases} \alpha(1-\gamma) & \hbox{if } x=0,\\ (1-\alpha) g(x, \mu, \phi)& \hbox{if } x\in(0,1)\\ \alpha\gamma & \hbox{if } x=1. \end{cases},\end{split}\]

where \(g(x,\mu,\phi)\) is the density of a (reparameterised) Beta distribution

\[g(x,\mu,\phi) =\frac{\Gamma(\phi)}{\Gamma(\mu \phi)\Gamma((1-\mu)\phi)} x^{\mu \phi -1}(1-x)^{(1-\mu)\phi -1}, \quad x\in(0,1).\]

The cumulative distribution function is given by

\[F(x) =(1 - \alpha) G(x, \mu, \phi) + \alpha B(x, \gamma),\]

where \(G(x, \mu, \phi)\), and \(B(x, \gamma),\) denote the cdf of a Beta and a Bernoulli distribution, respectively.

🔔 Random Facts 🔔

• The Zero-One Inflated Beta appears in any application where the variable of interest takes values on the closed interval [0,1]. In particular, it has been widely used to model proportions.

• It is a mixture distribution

• Some interesting applications of this distribution can be found here:

  • A Bayesian Zero-One Inflated Beta Model for Estimating Poverty in U.S. Counties

  • An Application of Zero-One Inflated Beta Regression Models for Predicting Health Insurance Reimbursement

  • Modeling Loss Given Default

  • Estimating plant abundance using inflated beta distributions: Applied learnings from a lichen–caribou ecosystem

Today’s bonus is a histogram showing the empirical distribution of the Bank of Italy’s recovery rates. This picture illustrates the fac that recovery rates take value on the closed interval [0,1].

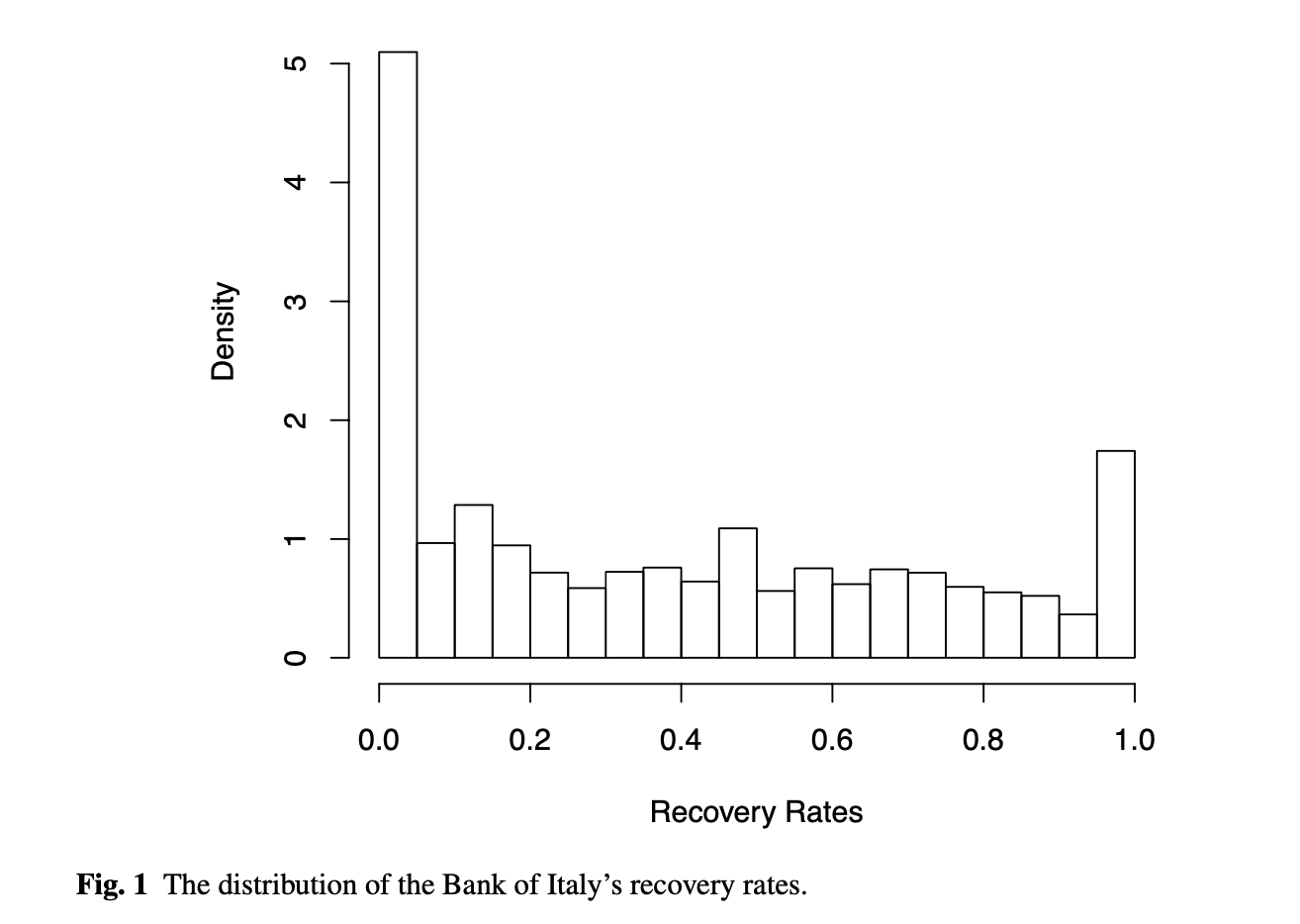
More about this plot: The Bank of Italy conducts a comprehensive survey on the loan recovery process of Italian banks in the years 2000-2001. Its purpose is to gather information on the main characteristics of the Italian recovery process and procedures, by collecting information about recovered amounts, recovery costs and timing. By means of a questionnaire, about 250 banks are surveyed. Since they cover nearly 90% of total domestic assets of 1999, the sample is representative of the Italian re- covery process. The database comprises 149,378 defaulted borrowers. Data concern individual loans which are privately held and not listed on the market. In particular, loans are towards Italian resident defaulted borrowers on the 31/12/1998 and written off by the end of 1999. Source: Raffaella Calabrese Raffaella Calabrese, 2012. Regression Model for Proportions with Probability Masses at Zero and One, Working Papers 201209, Geary Institute, University College Dublin.