Day 22 : Marchenko-Pastur Distribution

The Marchenko–Pastur distribution, or Marchenko–Pastur law, describes the asymptotic behavior of singular values of large rectangular random matrices. It is named after soviet mathematicians Volodymyr Marchenko and Leonid Pastur who published it in 1967 (Distribution of Eigenvalues for Some Sets of Random Matrices).

🔔 Random Facts 🔔

• The Marchenko-Pastur law was proved a little over a decade after the Wigner’s semicircle law but comes from a similar motivation. Instead of looking at the distribution of eigenvalues of a symmetric matrix, it looks at the distribution of eigenvalues of the covariance matrix of a given rectangular matrix.

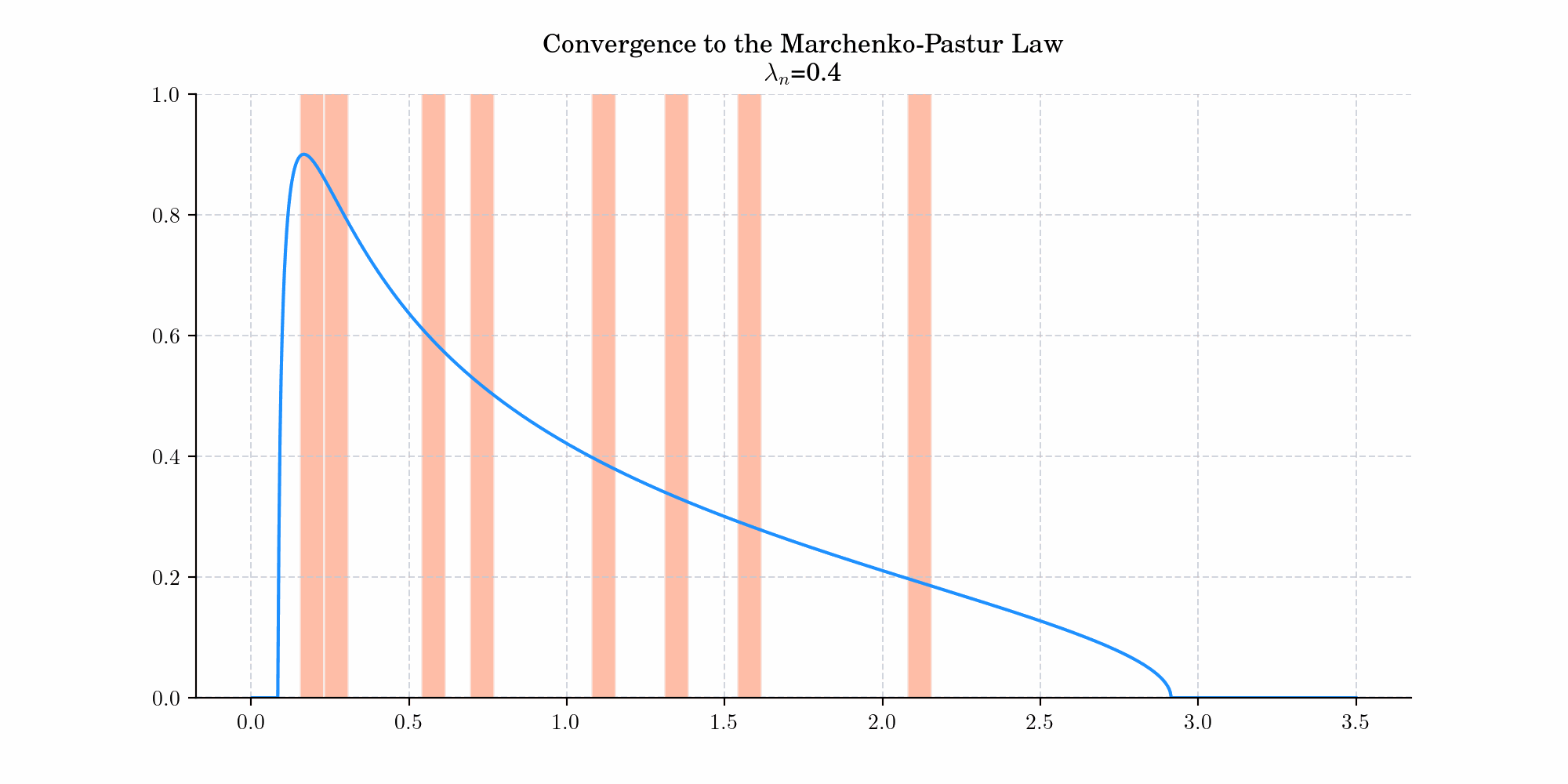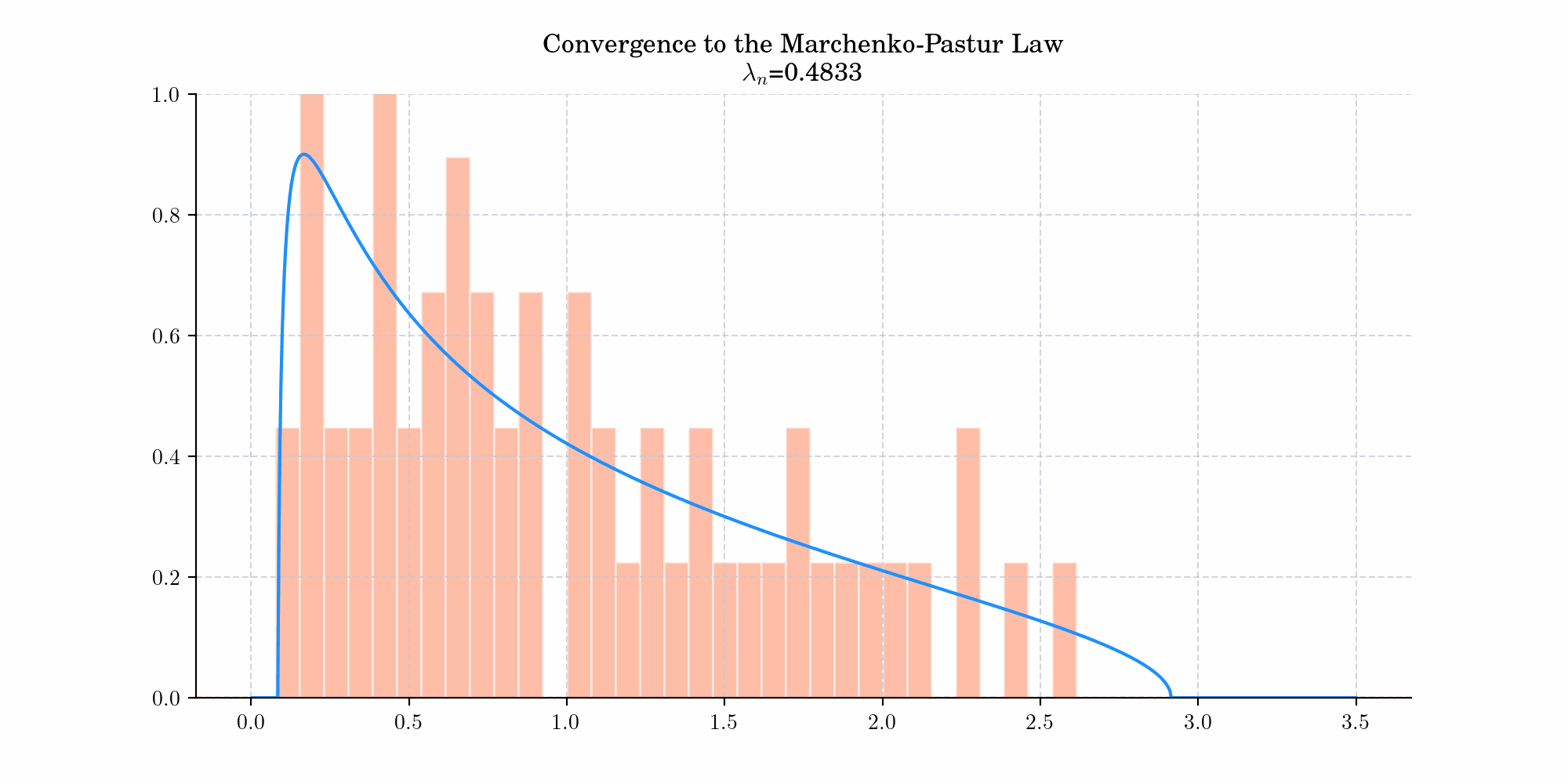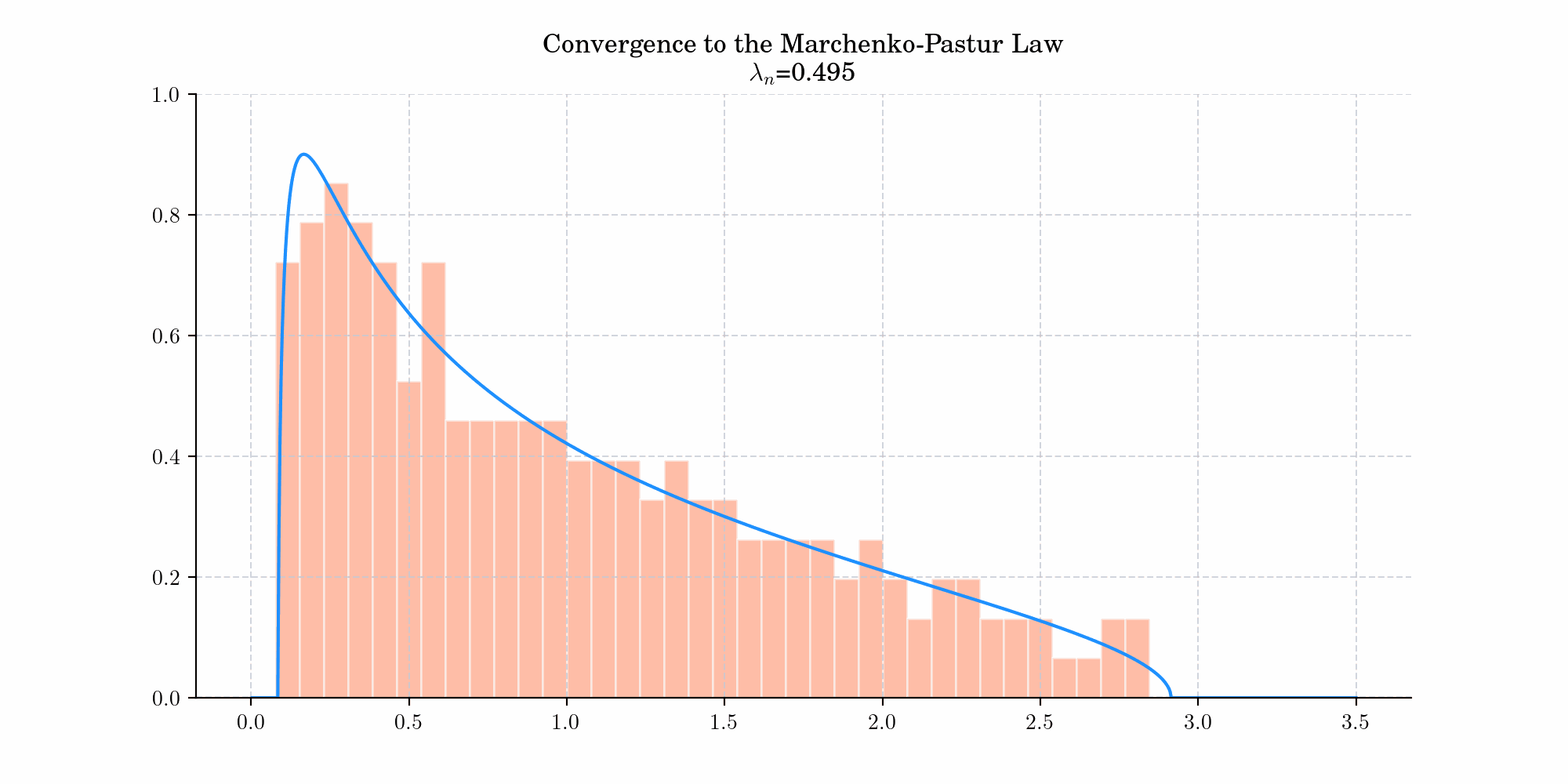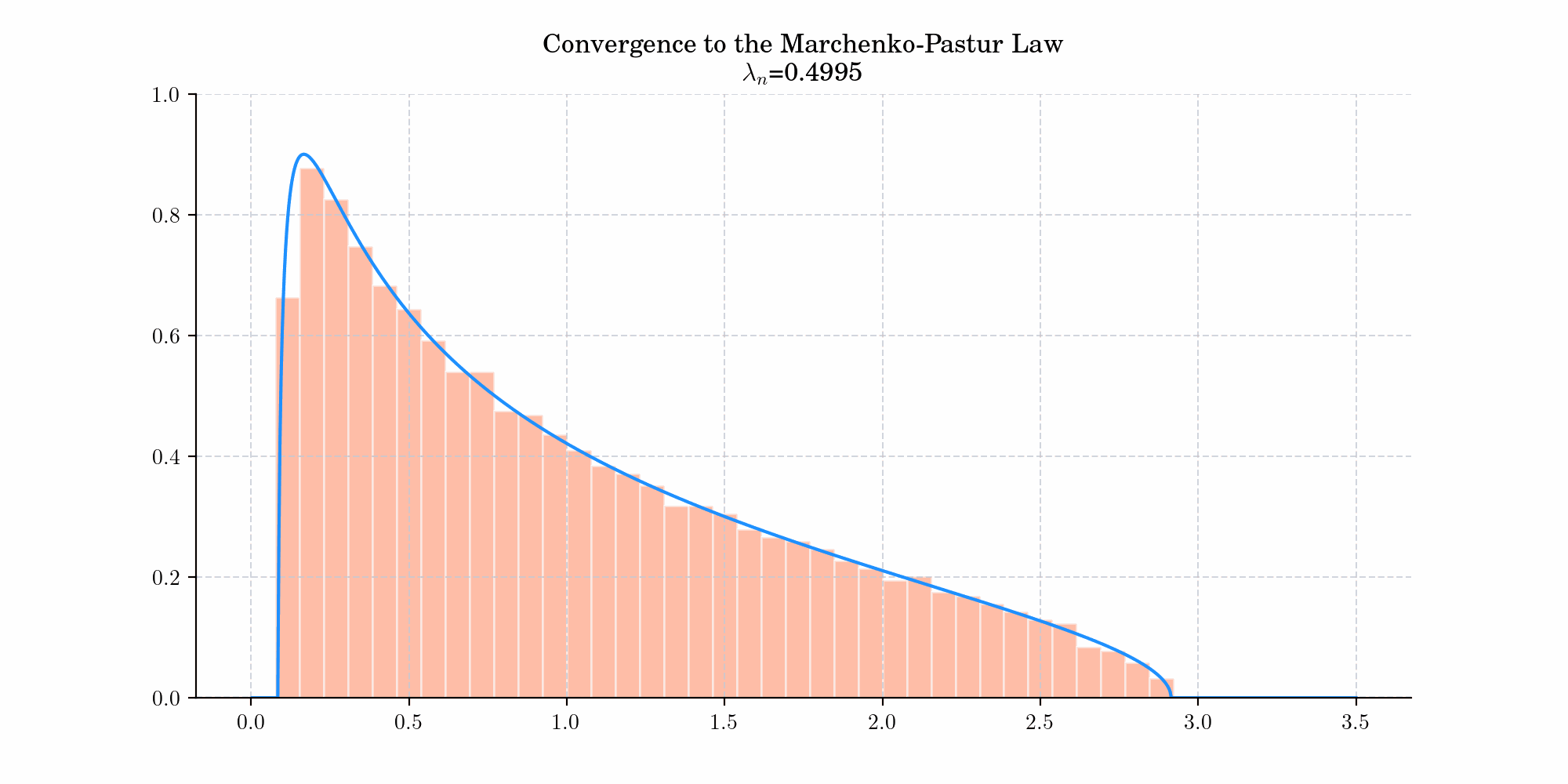
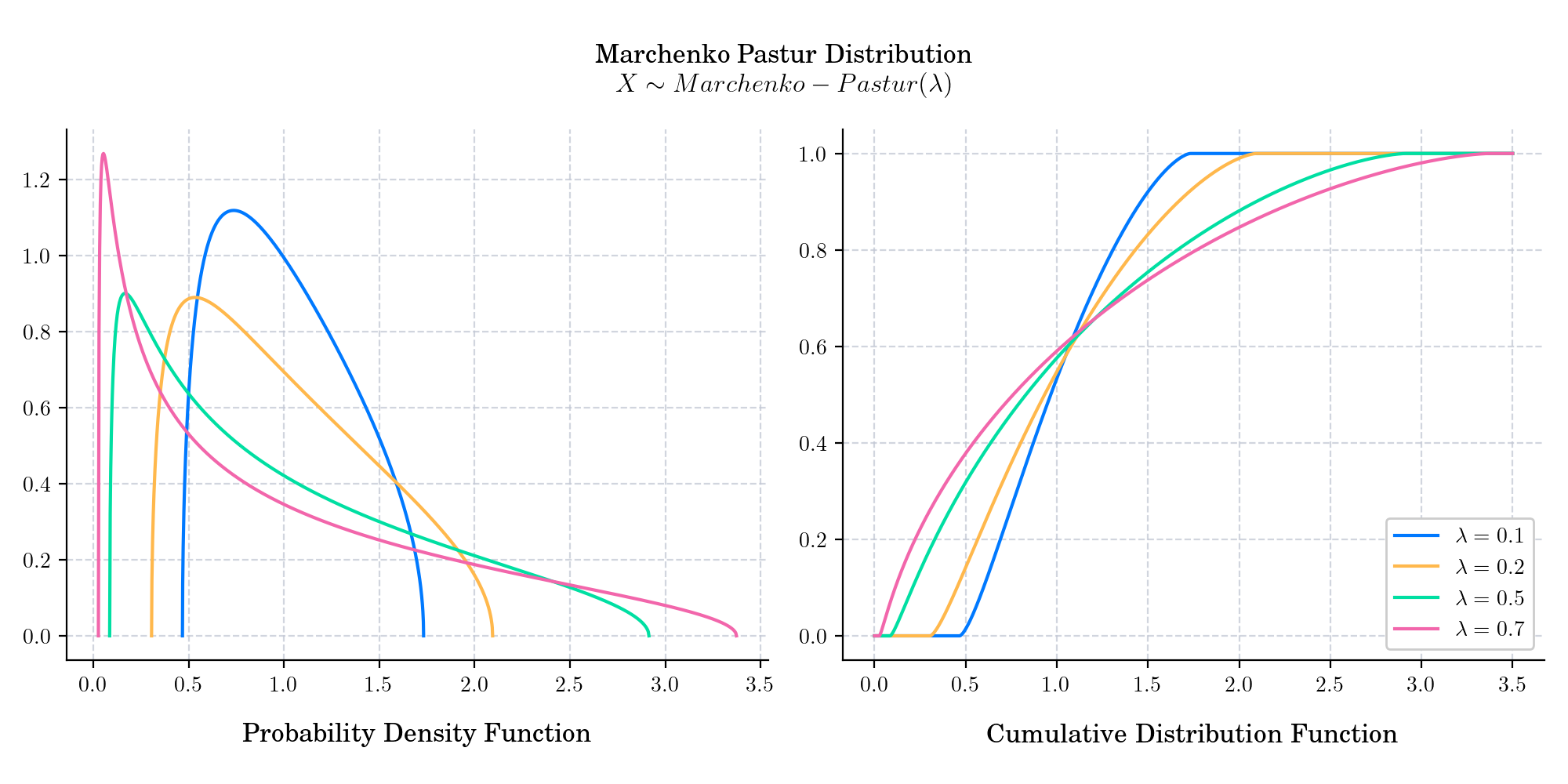
• If \(X\) denotes a \(m\times n\) random matrix whose entries are independent identically distributed random variables with zero mean and variance \(\sigma^2<\infty\), let $\(S_n = \frac{1}{n}XX^{t},\)\( and let \)\lambda_1, \cdots, \lambda_m\( be the eigenvalues of \)S_n\(. Assume that both \)m\(, and \)n\( tend to infinity so that the ratio \)m/n \rightarrow \lambda \in (0,1)\(. Then, the empirical spectral distribution \)F_n$ converges weakly to the Marchenko-Pastur distribution with density

\[f(x) = \frac{\sqrt{(b-x)(x-a)}}{2\pi x \lambda}, \quad x\in[a,b] ,\]

where \(a = \sigma^2 (1- \sqrt{\lambda})^2\) and \(b = \sigma^2 (1+\sqrt{\lambda})^2\).

• The Marchenko–Pastur law also arises as the free Poisson law in free probability theory, having rate \(1/\lambda\) and jump size \(\sigma^2\).

• The moments of the Marchenko-Pastur distribution are related to Narayana numbers which are famous numbers in combinatorics.

Today’s bonus is an animation showing the convergence to the Marchenko-Pastur law.