Day 9 : Gamma

The Gamma distribution is a two-parameter family of continuous probability distributions.

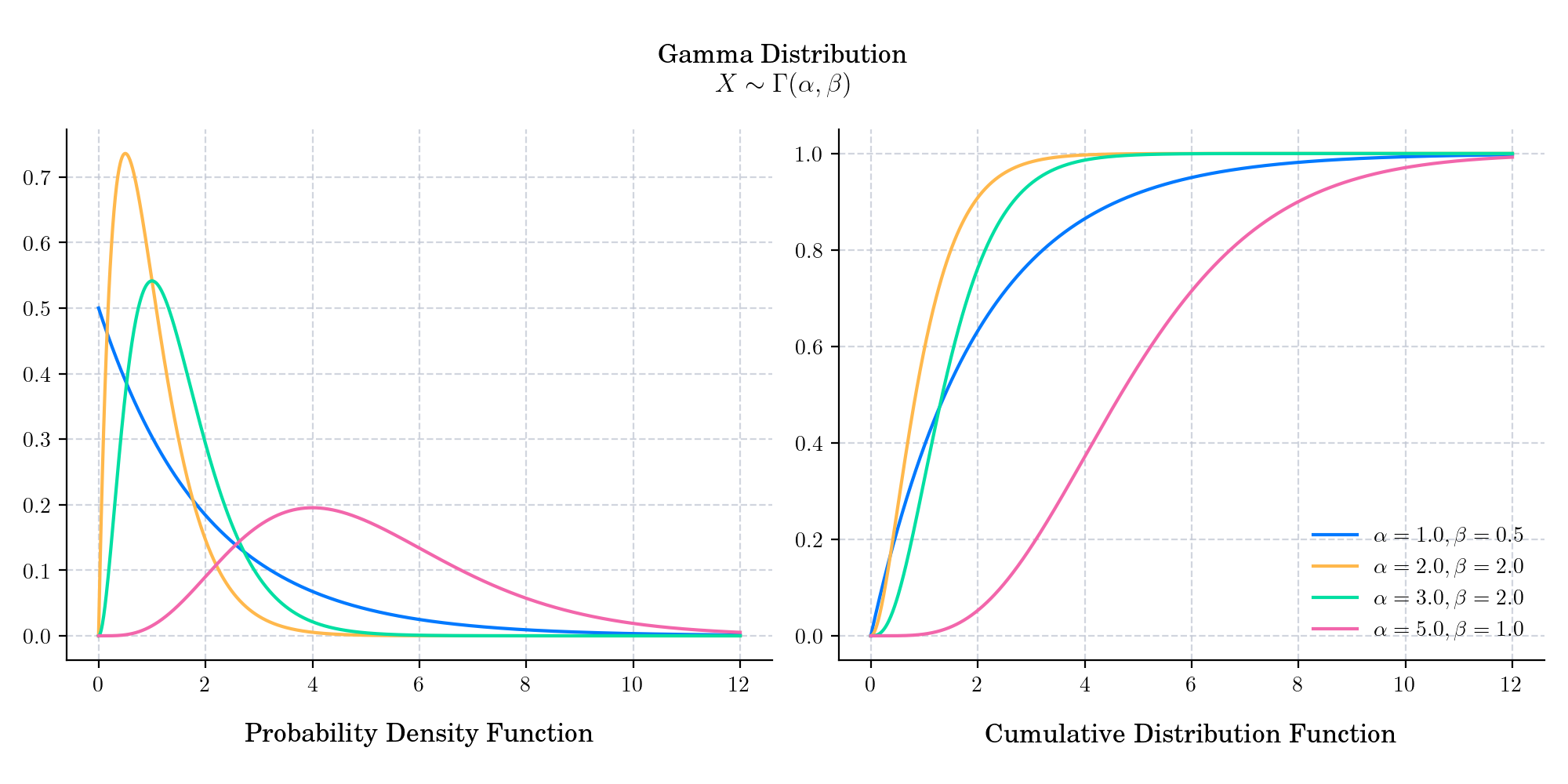
The probability density function is given by

\[f(x) =\frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}, \qquad x\geq 0.\]

The cumulative distribution function is given by

\[F(x) =\frac{1}{\Gamma(\alpha)} \gamma(\alpha, \beta x), , \qquad x\geq 0,\]

where \(\gamma(\alpha, \beta x)\) is the lower incomplete gamma function.

🔔 Random Facts 🔔

• The gamma distribution is widely used in Bayesian statistics as a conjugate prior. It is the conjugate prior for the precision (i.e. inverse of the variance) of a normal distribution. It is also the conjugate prior for the exponential distribution.

• The exponential distribution, Erlang distribution, and the chi-squared distribution are all special cases of the gamma distribution.