Day 15 : Chi

The chi distribution is a continuous probability distribution with support in \([0, \infty)\). It is the distribution of the positive square root of a sum of squared independent standard normal random variables. Equivalently, it is the distribution of the Euclidean distance between a multivariate Gaussian random variable and the origin. It is thus related to the Chi squared (Day 12) distribution by describing the distribution of the positive square roots of a random variable following a Chi squared distribution.

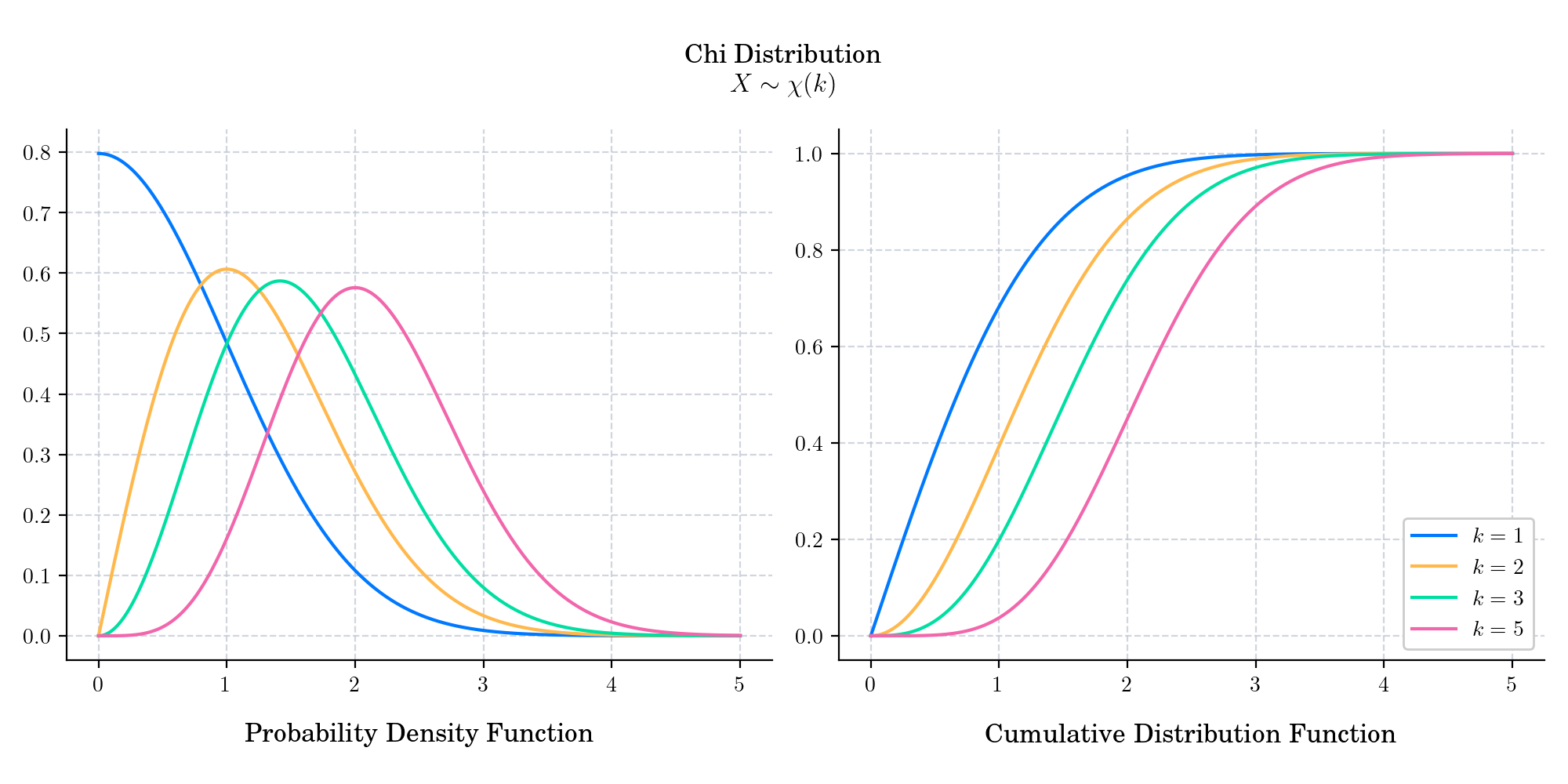
The probability density function is given by

\[f(x) = \frac{1}{2^{(k/2) - 1} \Gamma(k/2) } x^{k-1} e^{-x^2/2}, \qquad x\geq 0.\]

The cumulative distribution function is given by

\[F(x) = P(k/2, x^2/2) , \qquad x\geq 0,\]

where \(P\) is the regularized gamma function.

🔔 Random Facts 🔔

• The Chi distribution with \(k=2\) degrees of freedom is known as the Rayleigh distribution, named after British mathematician and physicist Lord Rayleigh — who won the Nobel Prize in Physics in 1904 “for his investigations of the densities of the most important gases and for his discovery of argon in connection with these studies.

• The Chi distribution with \(k=3\) degrees of freedom is known as the Maxwell–Boltzmann distribution. This distribution originated to describe particle speeds in idealized gases, where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment.

• If \(X\) follows a Chi distribution with \(k\) degrees of freedom, then \(X^2\) follows a Chi Squared distribution with the same degrees of freedom.

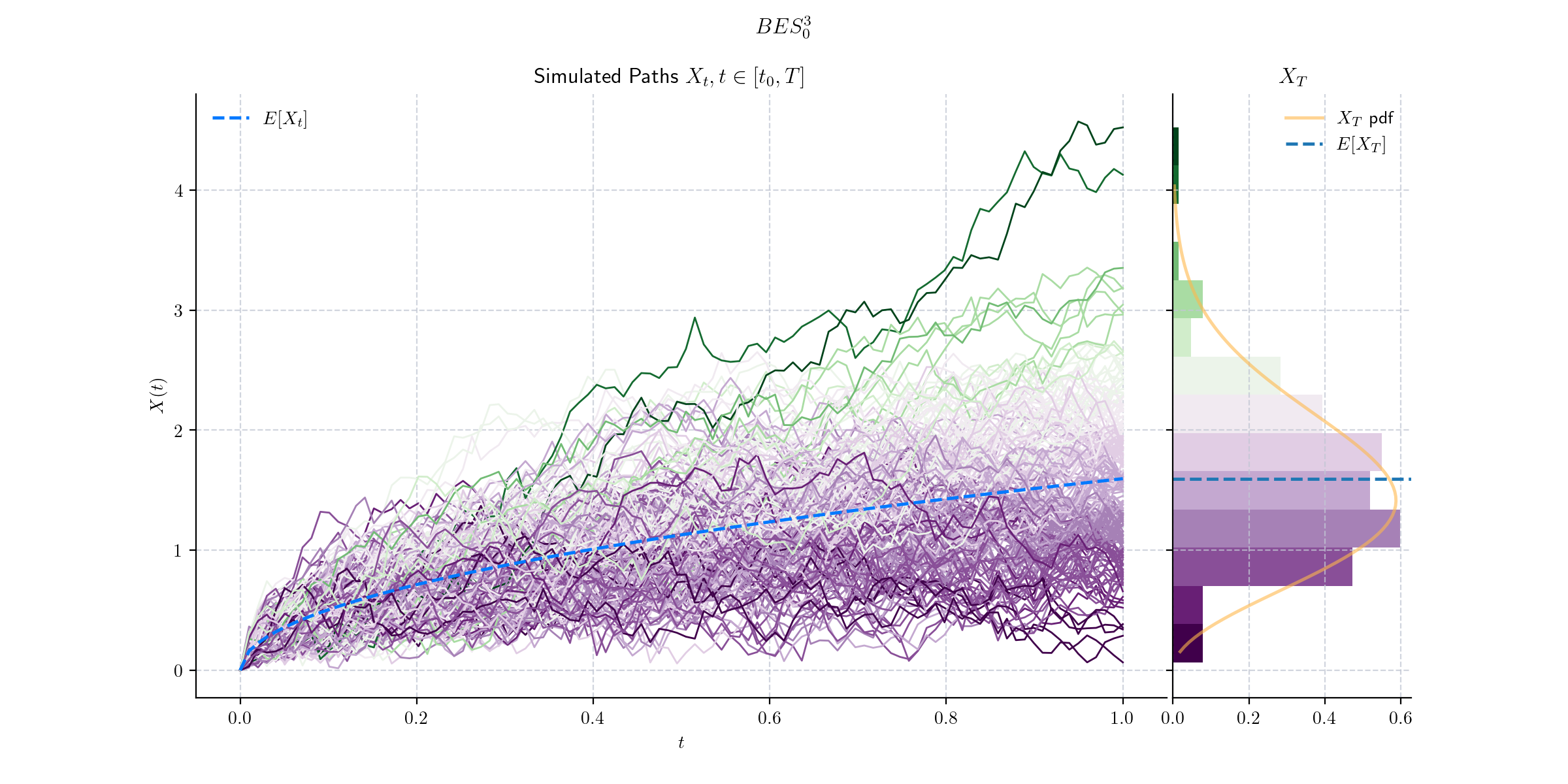
• The Chi distribution also arises in the context of Bessel processes.

Today’s bonus plot shows a simulation from a Bessel process of dimension 3. The marginal distribution on the right side follows a Chi distribution!