Day 20 : Tracy-Widom

Day 20 : Tracy-Widom#

The Tracy–Widom distribution is a probability distribution from random matrix theory introduced by American mathematicians Craig Tracy and Harold Widom in their paper On Orthogonal and Symplectic Matrix Ensembles (1995). It is the distribution of the normalized largest eigenvalue of a random Hermitian matrix.

🔔 Random Facts 🔔#

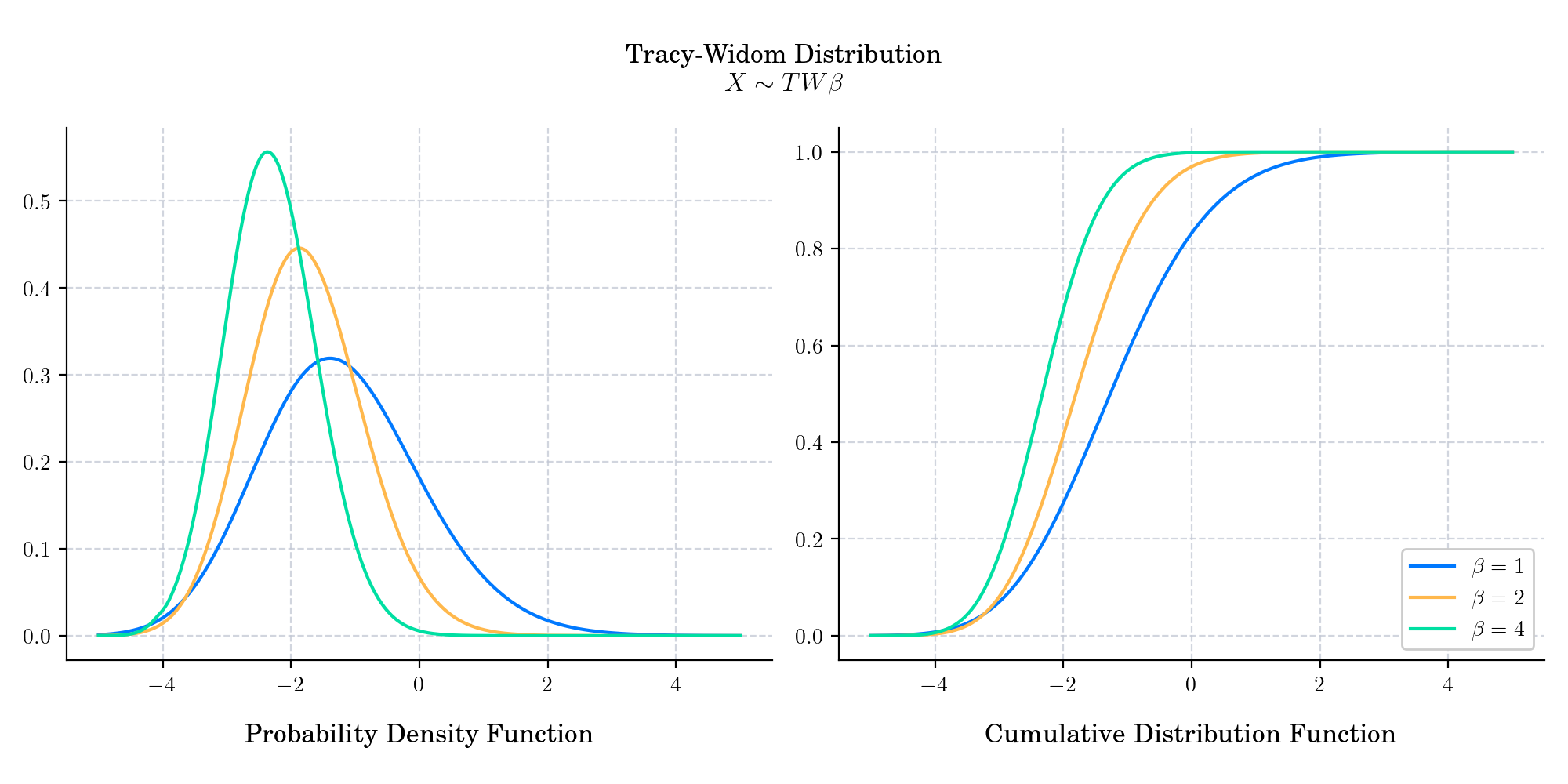
  • Let \(F_{\beta}\) denote the cumulative distribution function of the Tracy–Widom distribution with given \(\beta\). There are typically three Tracy–Widom distributions \(F_{\beta}\), with \(\beta\in\{1,2,4\}\). They correspond to the three Gaussian ensembles:

    • Gaussian orthogonal ensemble (\(\beta=1\)),

    • Gaussian unitary ensemble (\(\beta=2\))

    • Gaussian symplectic ensemble (\(\beta=4\)).

  • The Tracy-Widom distribution also appeared in the solution of a long standing problem from combinatorics, first raised by Ulam in the early 60s. Consider a permutation of the numbers 1, 2, … , N , picked uniformly at random from the N! such permutations. What is the probability distribution of the longest increasing subsequence of this permutation? In 1999, Baik, Deift, and Johansson proved that if \(l_n\) is the longest increasing subsequence, then as \(N\rightarrow \infty\), the distribution of

\[\frac{l_n - 2\sqrt{N}}{N^{1/6}},\]

converges to the Tracy-Widom distribution with \(\beta=2\). For details, see On the Distribution of the Length of the Longest Increasing Subsequence of Random Permutations (1998).

  • The Tracy-Widom distribution is not infinitely divisible. This was proved in 2017 by Mexican mathematician J.A. Domínguez-Molina. See “The Tracy-Widom distribution is not infinitely divisible”, Statistics & Probability Letters, 213 (1): 56–60, arXiv:1601.02898, doi:10.1016/j.spl.2016.11.029, S2CID 119676736.

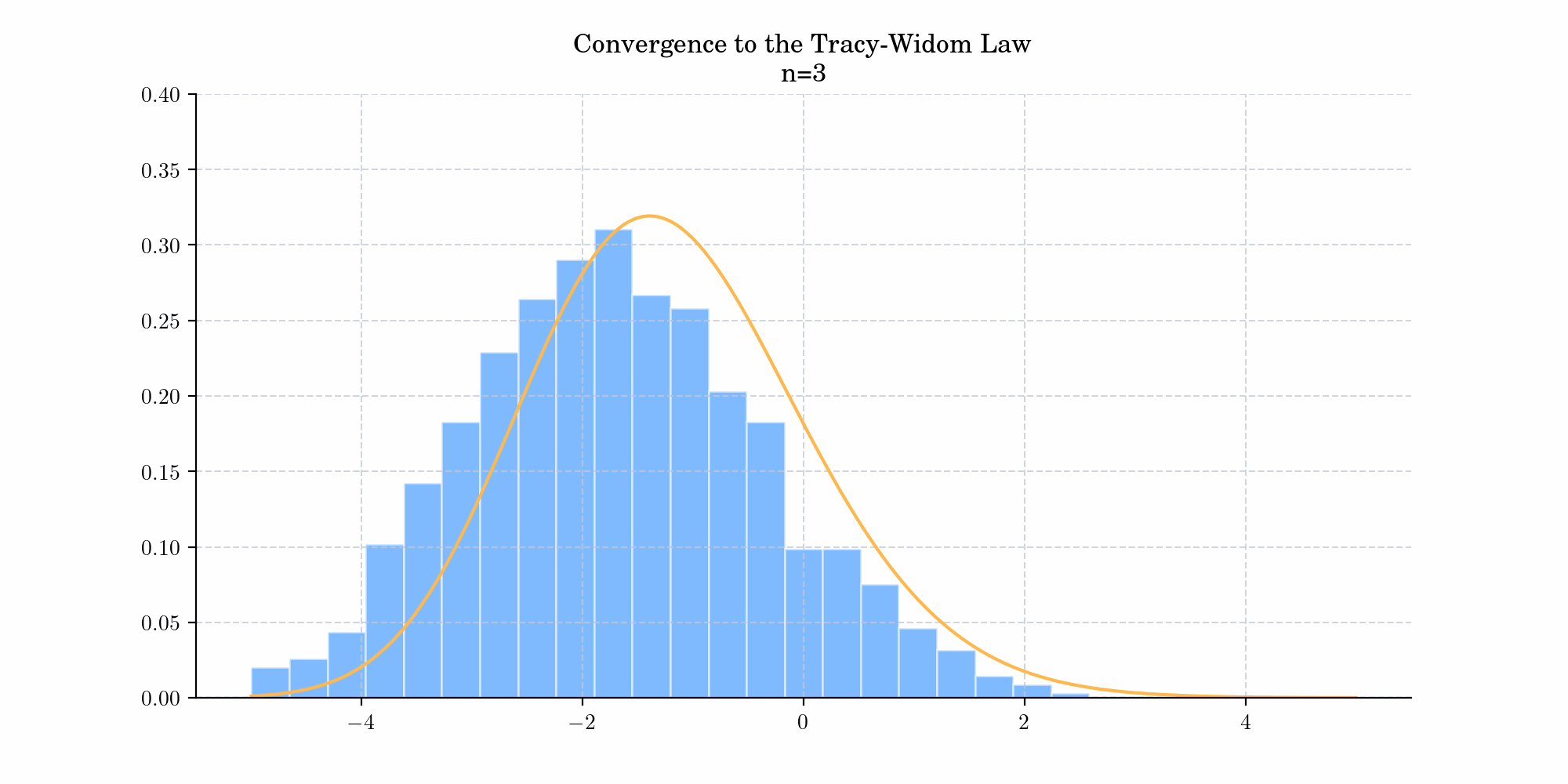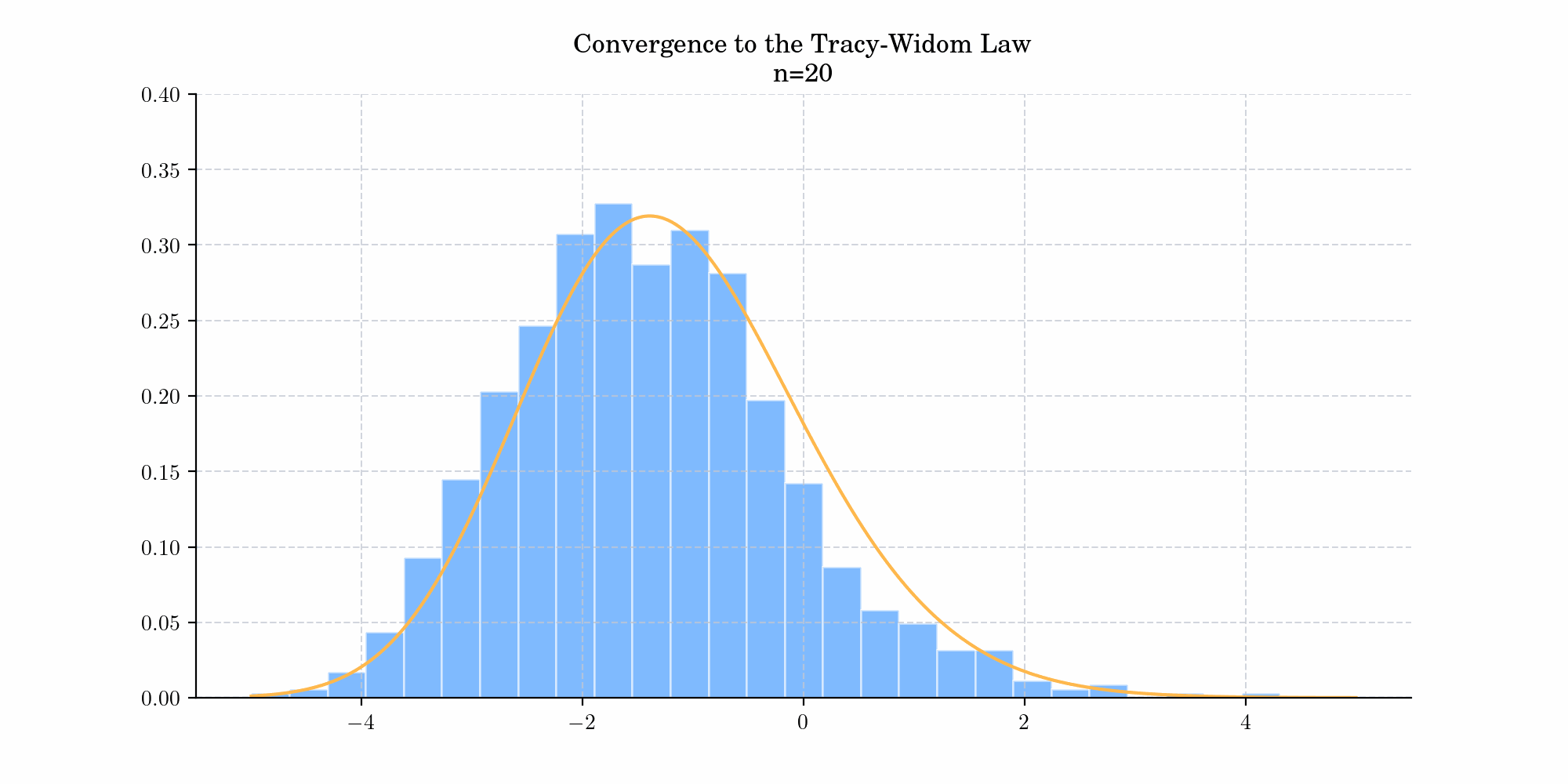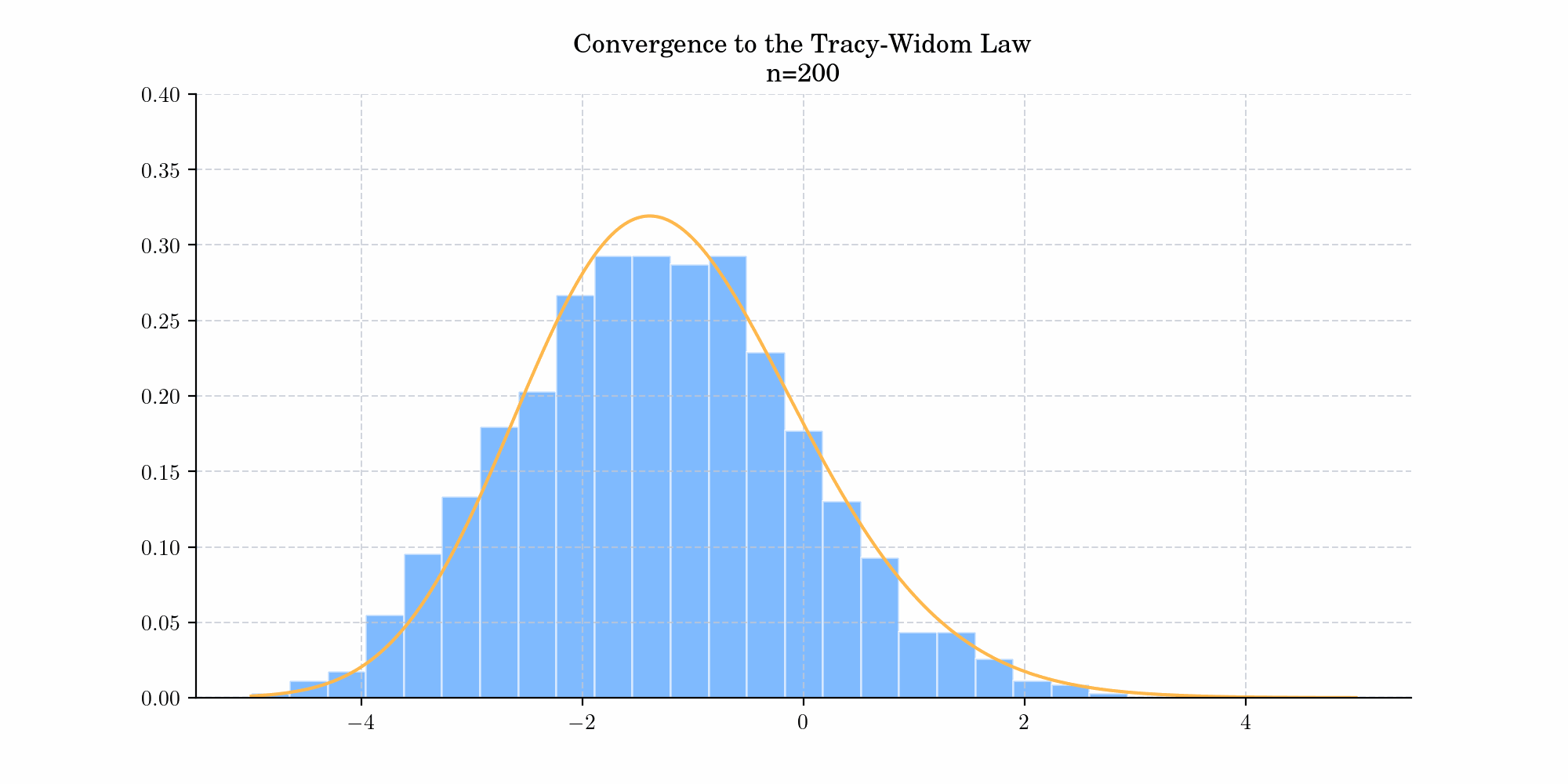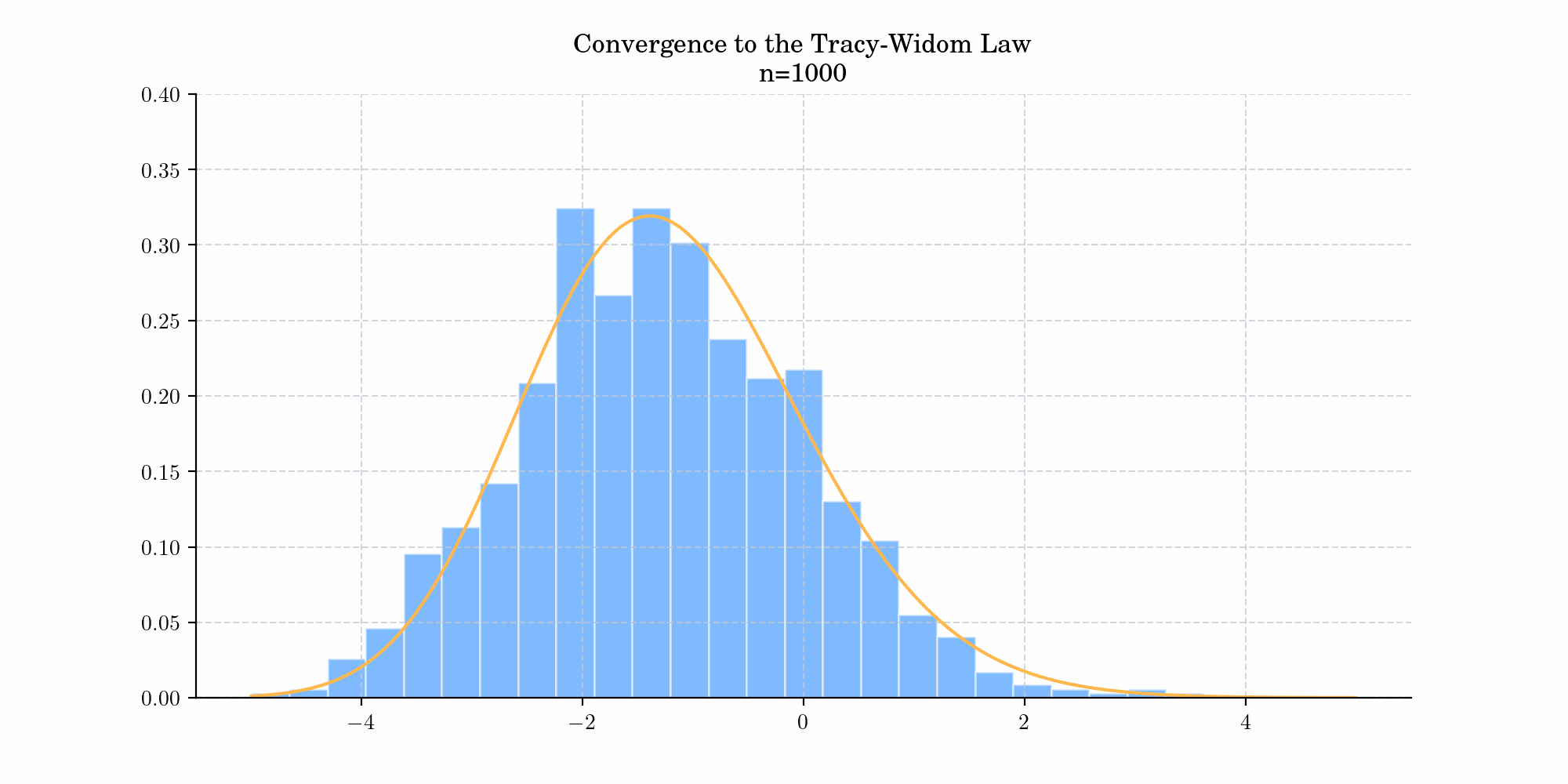
  • In general, consider a Gaussian ensemble, with its diagonal entries having variance 1, and off-diagonal entries having variance \(\sigma^2\), and let \(F_{n,\beta}(s)\) be probability that an \(n\times n\)matrix sampled from the ensemble have maximal eigenvalue \(\leq s\), then

\(F_{\beta }(x)=\lim _{N\to \infty }F_{N,\beta }(\sigma (2N^{1/2}+N^{-1/6}x))=\lim _{N\to \infty }Pr(N^{1/6}(\lambda _{max}/\sigma -2N^{1/2})\leq x)\)

where \(\lambda_{\max}\) denotes the largest eigenvalue of the random matrix. Today’s bonus shows a simulation demonstrating this convergence.

Also, a really nice article about the Tracy-Widom distribution: At the Far Ends of a New Universal Law

Contents