Day 5 : Poisson

Day 5 : Poisson#

The Poisson distribution is a discrete probability distribution with support \(k\in\mathbb{N}_0\) (the natural numbers starting from zero) that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson. It is defined by a parameter λ>0, which is called rate.

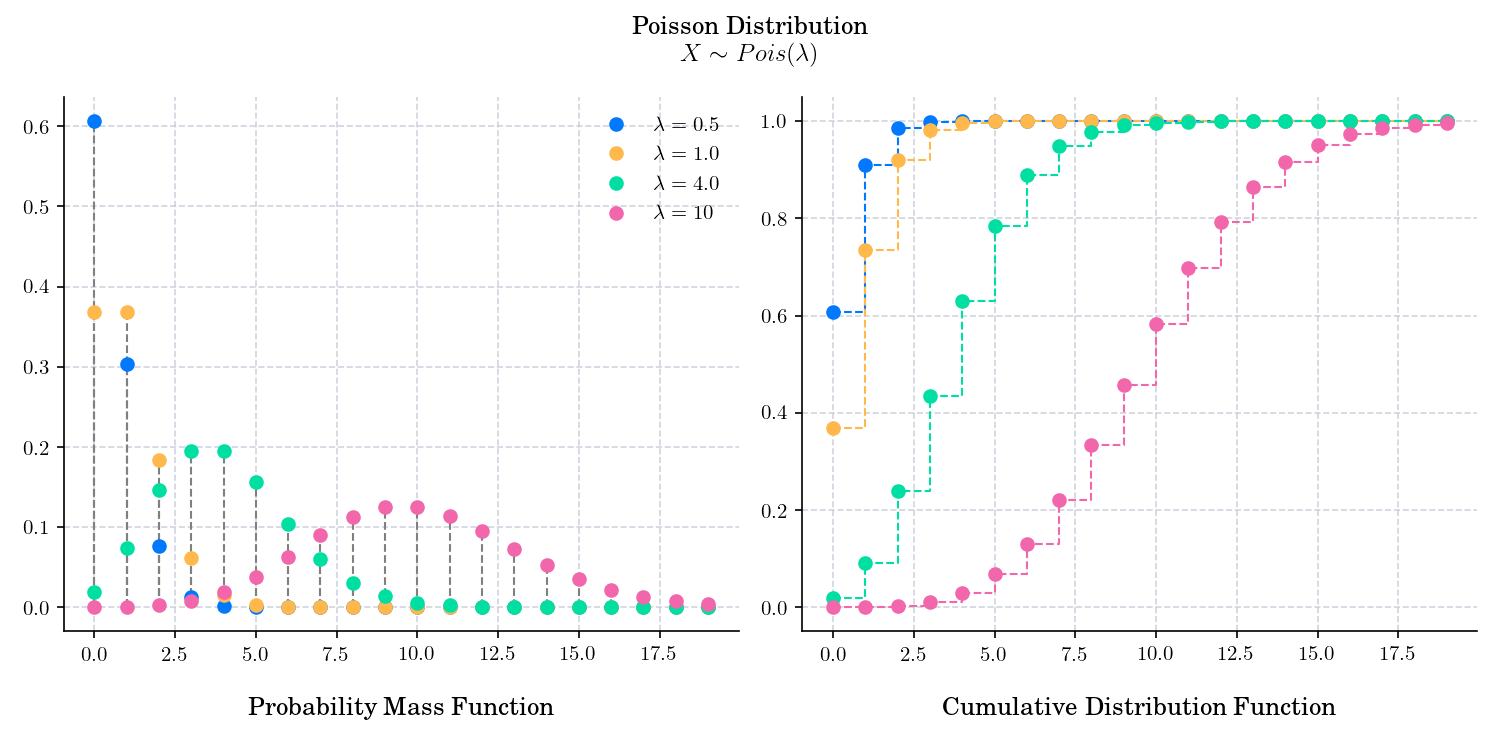
The probability mass function is given by

\[f(k) = \frac{ \lambda^k e^{-\lambda}}{k!}.\]

The cumulative distribution function is given by

\[F(k) = e^{-\lambda} \sum_{j=0}^{\lfloor k \rfloor }\frac{\lambda^{j}}{j!}.\]

🔔 Random Facts 🔔#

  • The expected value and variance of a Poisson-distributed random variable are both equal to its parameter λ. This is probably the most well-known property of the Poisson distribution ✅

  • The Poisson distribution can be used to model the arrival of new buy or sell orders entered into the market 🏪 or the expected arrival of orders at specified trading venues or dark pools. In these cases, the Poisson distribution is used to provide expectations surrounding confidence bounds around the expected order arrival rates.

Contents