Day 12 : Chi Squared#

The chi-squared distribution (also called chi-square) with $k > 0,$ degrees of freedom is the distribution of the sum of the squares of $k$ independent standard normal random variables.

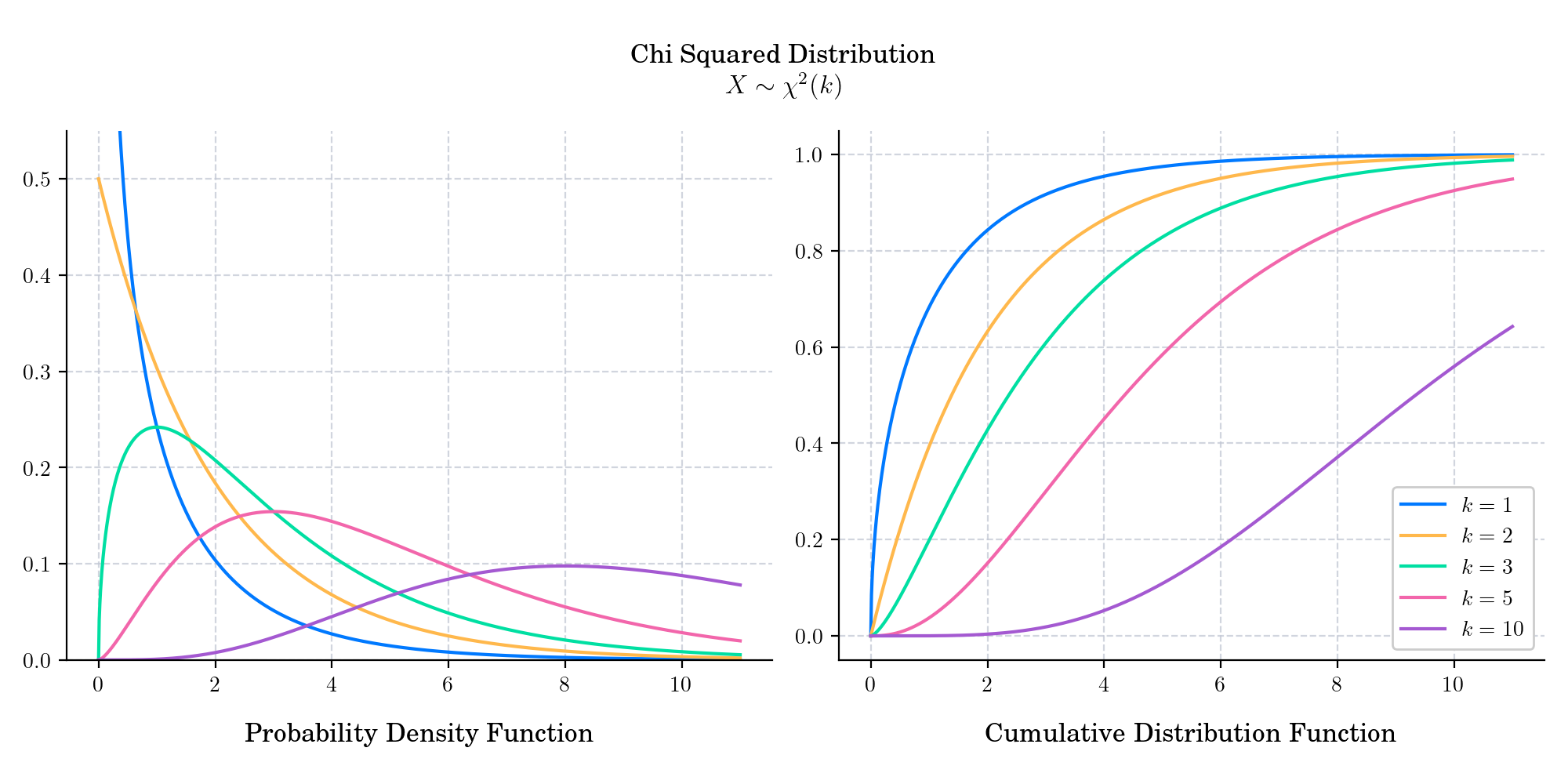
The probability density function is given by

f (x) = \frac{1}{2^{k / 2} Γ (k / 2)} x^{k / 2 - 1} e^{- x / 2}, x \geq 0,

where $Γ$ is the Gamma function.

The cumulative distribution function is given by

F (x) = \frac{1}{Γ (k / 2)} γ (\frac{k}{2}, \frac{x}{2}), x \geq 0,

where $γ$ is the lower incomplete gamma function.

🔔 Random Facts 🔔#

It converges to a normal distribution for large $k$ (by the central limit theorem). For many practical purposes, for $k > 50$ the distribution is sufficiently close to a normal distribution.
It is a special case of the Gamma distribution (Day 9) and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing, and confidence intervals for population variance when the underlying distribution is normal.
The sum of independent chi-squared variables is also chi-squared distributed. Specifically, if $X_{i}, i = 1, \dots n$ , are independent chi-squared random variables with $k_{i}, i = 1, \dots, n$ degrees of freedom, respectively, then $Y = X_{1} + \dots + X_{n}$ is chi-squared distributed with $k = k_{1} + \dots + k_{n}$ degrees of freedom.

Day 12 : Chi Squared

Contents

Day 12 : Chi Squared#

🔔 Random Facts 🔔#