Day 18 : Wigner Semicircle

The Wigner semicircle distribution, named after the Hungarian-American theoretical physicist Eugene Wigner, is the probability distribution on [−_R_, R] whose probability density function is a scaled semicircle centered at (0, 0). The parameter R is commonly referred to as the “radius” parameter of the distribution.

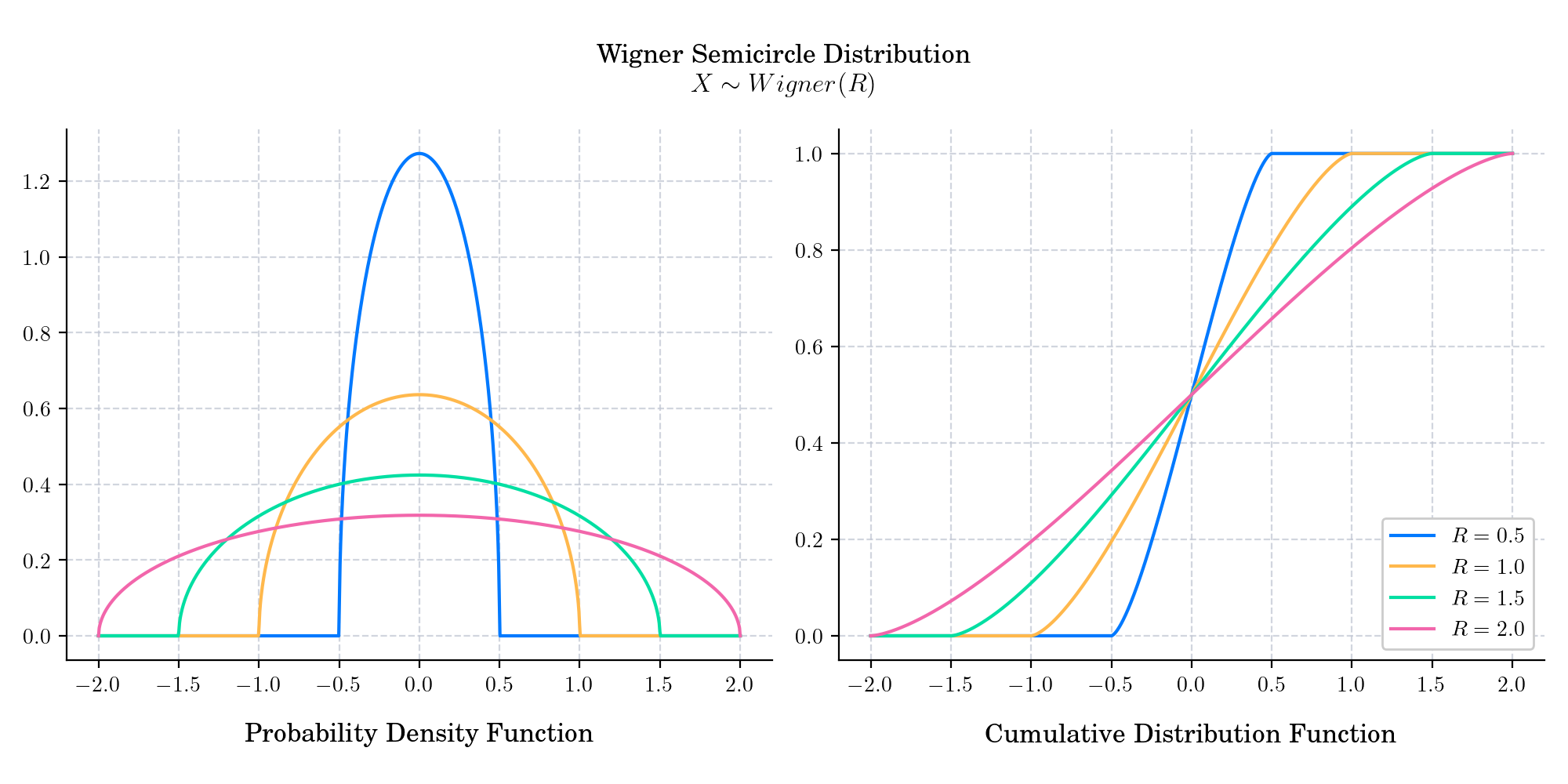
The probability density function is given by

\[f(x) = \frac{2}{\pi R^2} \sqrt{R^2 - x^2},\]

The cumulative distribution function is given by

\[F(x) =\frac{1}{2} + \frac{x\sqrt{R^2 - x^2}}{\pi R^2} + \frac{\arcsin\left(\frac{x}{R}\right) }{\pi}.\]

🔔 Random Facts 🔔

• The Wigner distribution coincides with a scaled beta distribution. That is, if Y is a beta-distributed random variable with parameters α = β = 3/2, then the random variable X = 2_RY_ – R follows a Wigner semicircle distribution with radius R.

• In free probability theory, the role of Wigner’s semicircle distribution is analogous to that of the normal distribution in classical probability theory. Namely, in free probability theory, the role of cumulants is occupied by “free cumulants”, whose relation to ordinary cumulants is simply that the role of the set of all partitions of a finite set in the theory of ordinary cumulants is replaced by the set of all noncrossing partitions of a finite set. Just as the cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is normal, so also, the free cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is Wigner’s semicircle distribution.

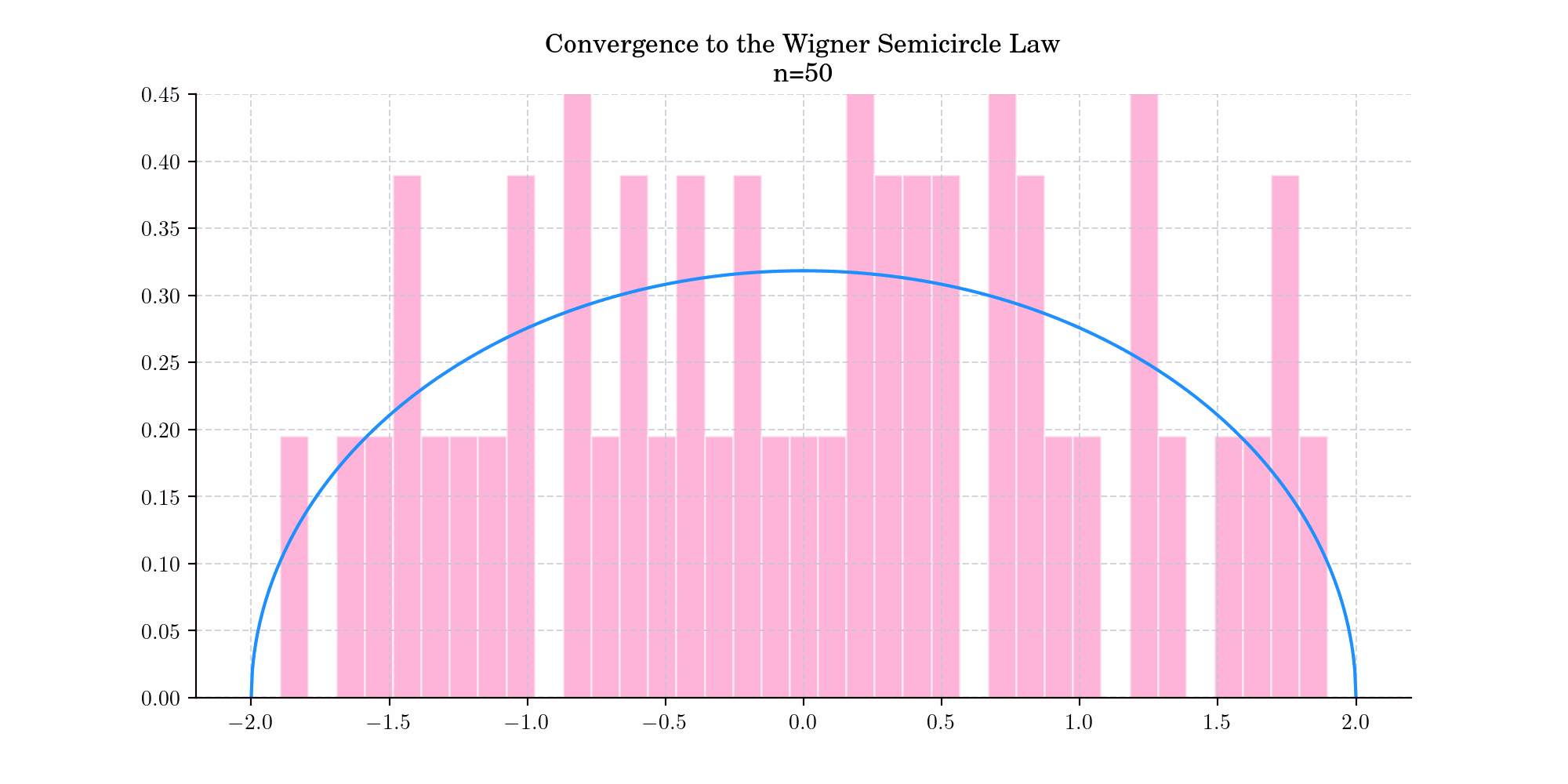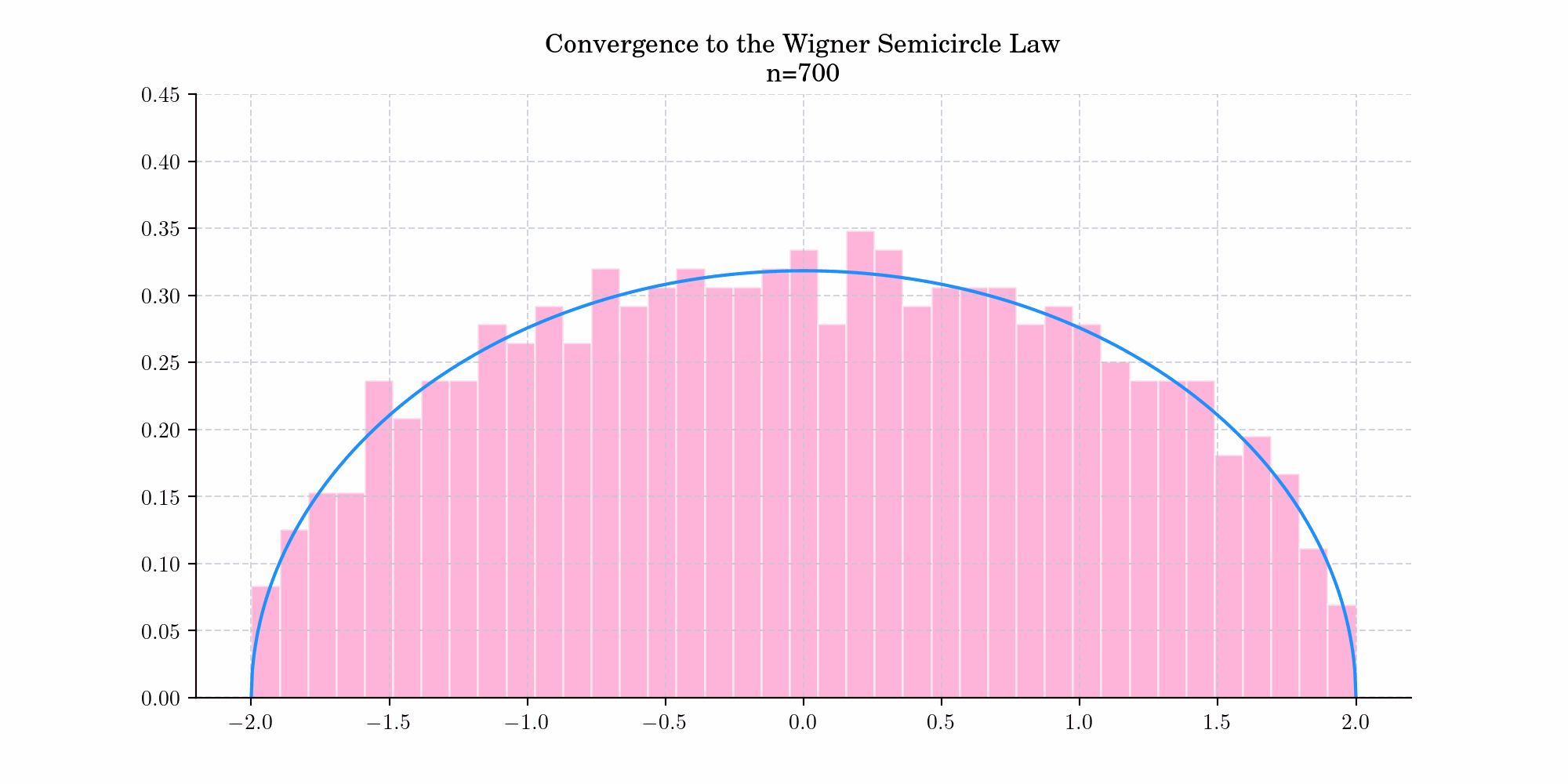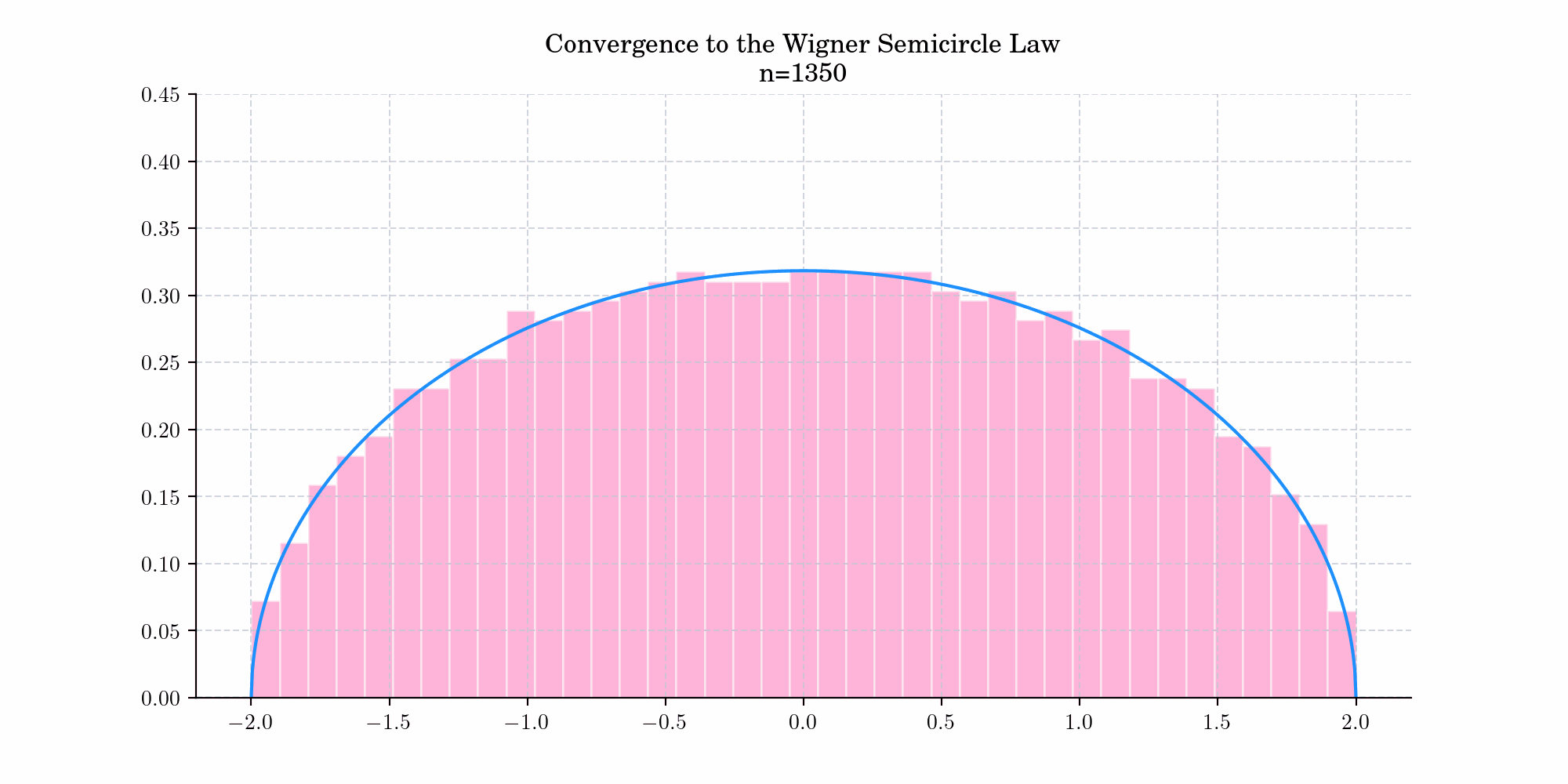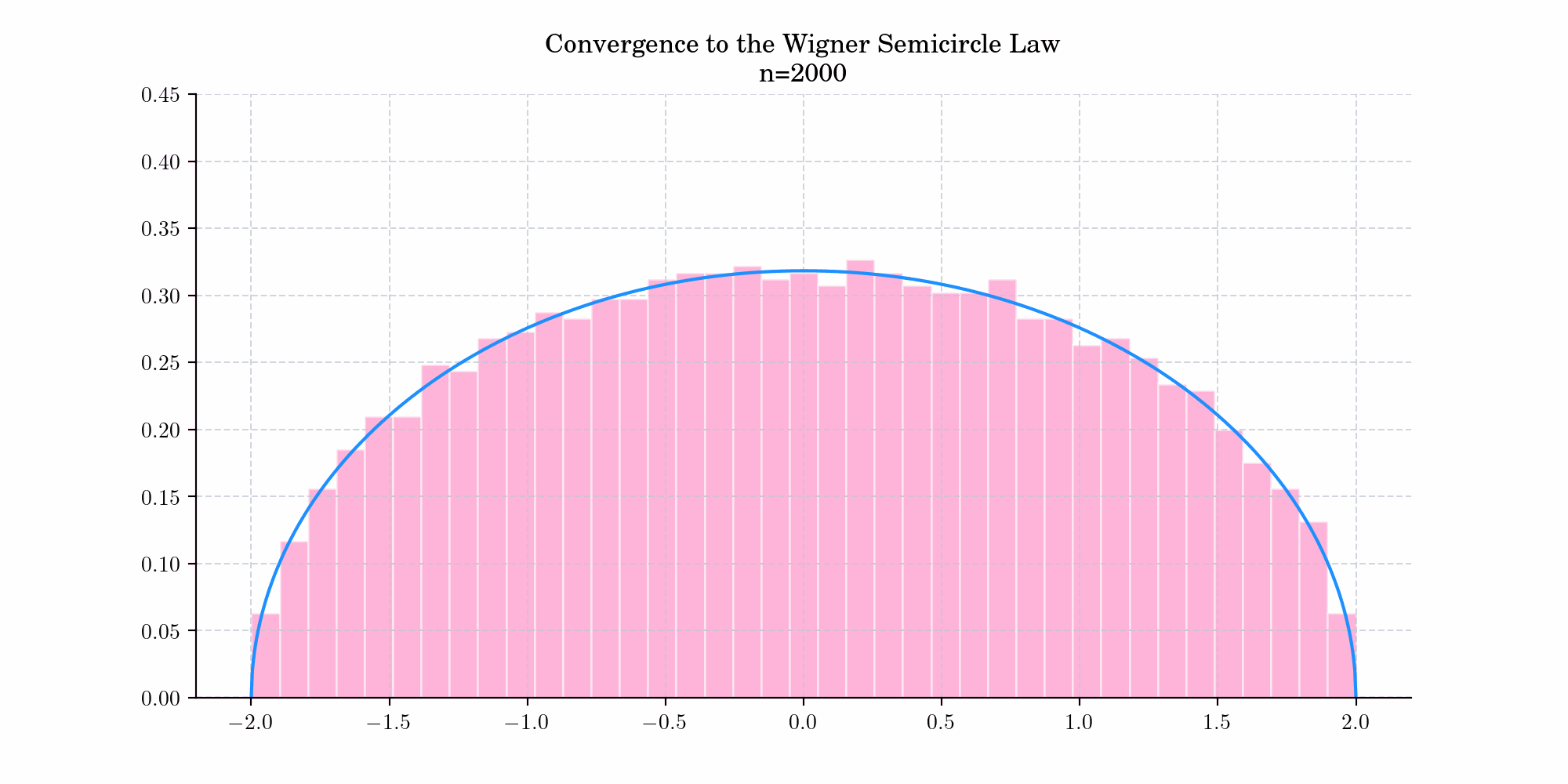
• The distribution arises as the limiting distribution of the eigenvalues of many random symmetric matrices, that is, as the dimensions of the random matrix approach infinity. This is known as the Semicircle Law and was first observed by Wigner (1955) for certain special classes of random matrices arising in quantum mechanical investigations. Today’s bonus shows a simulation demonstrating this convergence.