Discretisation Schemes

• 
• 

# Author: Dialid Santiago <d.santiago@outlook.com>
# License: MIT
# Description: Advent Calendar 2025 - Plot GBM via Transformation of BM

import matplotlib.pyplot as plt
import numpy as np
from aleatory.processes import BrownianMotion
from aleatory.styles import qp_style
qp_style()  # Use quant-pastel-style


def gbm_exact(S0, mu, sigma, T, N, seed=None):
    if seed is not None:
        np.random.seed(seed)
    dt = T / N
    W = np.sqrt(dt) * np.random.randn(N)
    t = np.linspace(0, T, N + 1)
    S = np.zeros(N + 1)
    S[0] = S0

    for i in range(N):
        S[i+1] = S[i] * np.exp(
            (mu - 0.5 * sigma**2) * dt + sigma * W[i]
        )

    return t, S


def gbm_euler(S0, mu, sigma, T, N, dW):
    dt = T / N
    S = np.zeros(N + 1)
    S[0] = S0

    for i in range(N):
        S[i+1] = (
            S[i]
            + mu * S[i] * dt
            + sigma * S[i] * dW[i]
        )

    return S


def gbm_milstein(S0, mu, sigma, T, N, dW):
    dt = T / N
    S = np.zeros(N + 1)
    S[0] = S0

    for i in range(N):
        S[i+1] = (
            S[i]
            + mu * S[i] * dt
            + sigma * S[i] * dW[i]
            + 0.5 * sigma**2 * S[i] * (dW[i]**2 - dt)
        )

    return S


# Parameters
S0 = 100
mu = 0.05
sigma = 0.3
T = 1.0
N = 100
seed = 42

# Common Brownian increments
np.random.seed(seed)
dt = T / N
dW = np.sqrt(dt) * np.random.randn(N)

# Simulation
t, S_exact = gbm_exact(S0, mu, sigma, T, N, seed=seed)
S_euler = gbm_euler(S0, mu, sigma, T, N, dW)
S_milstein = gbm_milstein(S0, mu, sigma, T, N, dW)


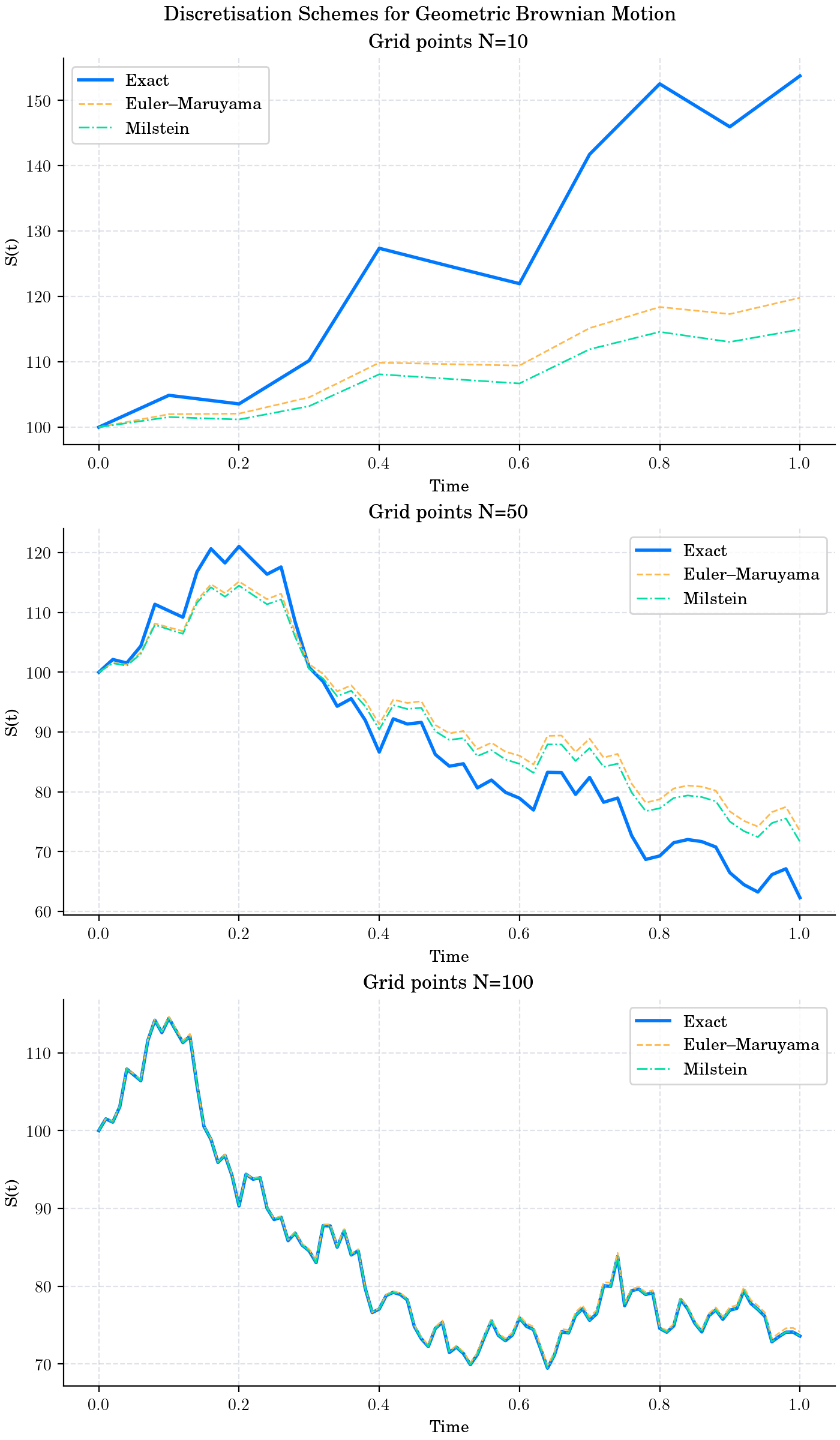
fig, axs = plt.subplots(3, 1, figsize=(7, 12), layout="constrained")

for N, ax in zip([10, 50, 100], [axs[0], axs[1], axs[2]]):
    t, S_exact = gbm_exact(S0, mu, sigma, T, N, seed=seed)
    S_euler = gbm_euler(S0, mu, sigma, T, N, dW[:N])
    S_milstein = gbm_milstein(S0, mu, sigma, T, N, dW[:N])
    ax.plot(t, S_exact, label="Exact", lw=2)
    ax.plot(t, S_euler, "--", label="Euler–Maruyama")
    ax.plot(t, S_milstein, "-.", label="Milstein")
    ax.set_title(f"Grid points N={N}")
    ax.set_xlabel("Time")
    ax.set_ylabel("S(t)")
    ax.legend()

fig.suptitle("Discretisation Schemes for Geometric Brownian Motion")
plt.show()





# --- Model parameters ---
S0 = 100.0
mu = 0.05
sigma = 0.3
T = 1.0

# --- Monte Carlo parameters ---
M = 5000          # number of paths
N_ref = 2**12     # fine grid for reference solution
dt_ref = T / N_ref

# Coarse step sizes
N_values = [2**k for k in range(4, 10)]  # 16 ... 512
dt_values = [T / N for N in N_values]

# --- Storage ---
errors_euler = []
errors_milstein = []

np.random.seed(42)

for N in N_values:
    dt = T / N
    ratio = N_ref // N

    err_euler = 0.0
    err_mil = 0.0

    for _ in range(M):
        # Fine Brownian increments
        dW_fine = np.sqrt(dt_ref) * np.random.randn(N_ref)

        # Aggregate increments for coarse grid
        dW_coarse = dW_fine.reshape(N, ratio).sum(axis=1)

        # --- Exact solution ---
        W_T = dW_fine.sum()
        S_exact = S0 * np.exp(
            (mu - 0.5 * sigma**2) * T + sigma * W_T
        )

        # --- Euler scheme ---
        S_e = S0
        for dW in dW_coarse:
            S_e += mu * S_e * dt + sigma * S_e * dW

        # --- Milstein scheme ---
        S_m = S0
        for dW in dW_coarse:
            S_m += (
                mu * S_m * dt
                + sigma * S_m * dW
                + 0.5 * sigma**2 * S_m * (dW**2 - dt)
            )

        err_euler += abs(S_e - S_exact)
        err_mil += abs(S_m - S_exact)

    errors_euler.append(err_euler / M)
    errors_milstein.append(err_mil / M)

# --- Plot ---
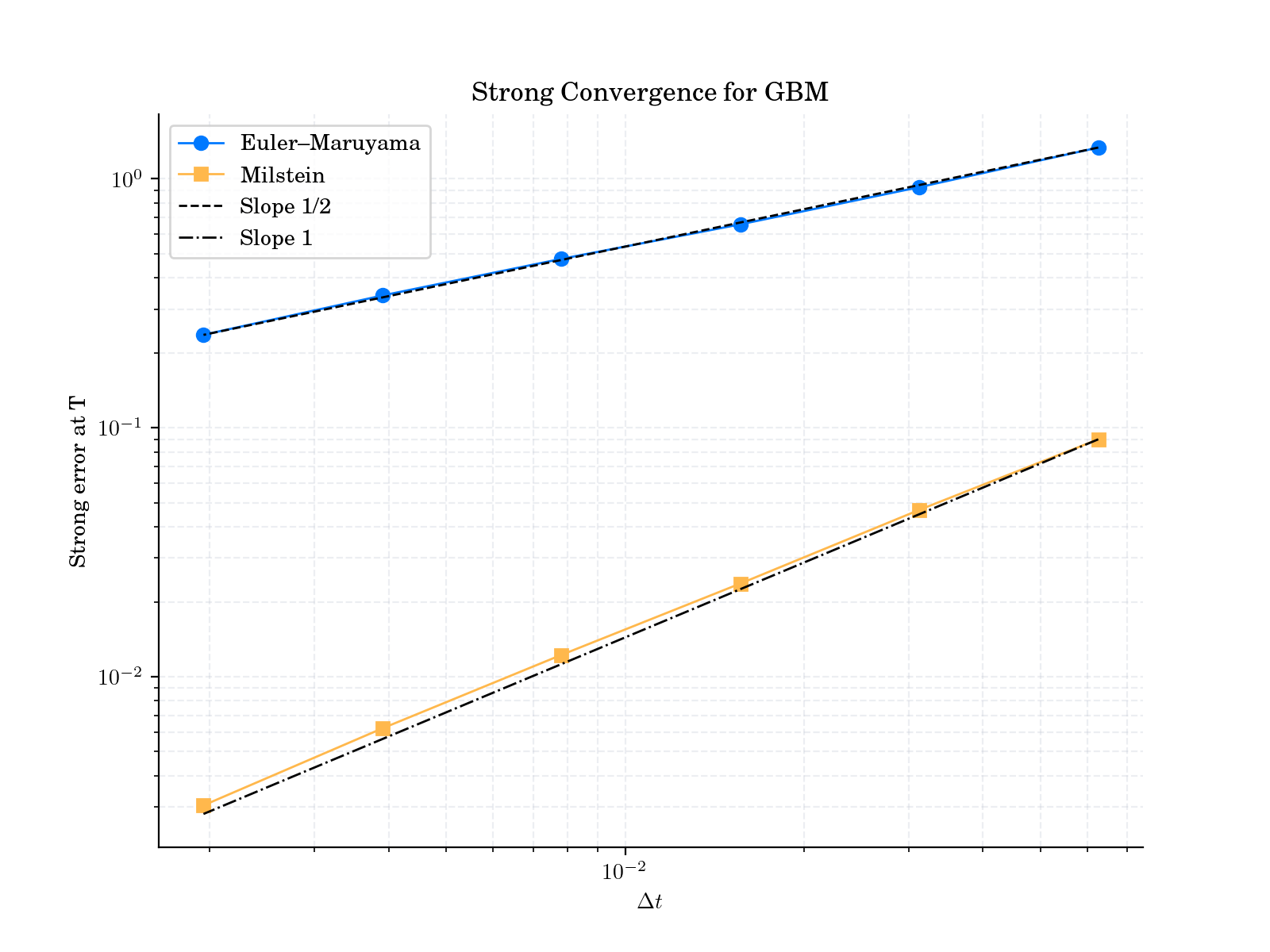
plt.figure(figsize=(8, 6))
plt.loglog(dt_values, errors_euler, "o-", label="Euler–Maruyama")
plt.loglog(dt_values, errors_milstein, "s-", label="Milstein")

# Reference slopes
plt.loglog(
    dt_values,
    errors_euler[0] * (np.array(dt_values) / dt_values[0])**0.5,
    "k--",
    label="Slope 1/2",
)
plt.loglog(
    dt_values,
    errors_milstein[0] * (np.array(dt_values) / dt_values[0]),
    "k-.",
    label="Slope 1",
)

plt.xlabel(r"$\Delta t$")
plt.ylabel("Strong error at T")
plt.title("Strong Convergence for GBM")
plt.legend()
plt.grid(True, which="both", alpha=0.3)
plt.show()