Day 18: Martingale

Day 18: Martingale#

“A financial market is viable (i.e., does not offer arbitrage opportunities) if and only if there exists a probability measure under which the realized stochastic process of discounted asset prices is a martingale. ” ― First Fundamental Theorem of Asset Pricing

Definition#

A stochastic process \(X = \{X_t, t \geq 0\}\) defined on a probability space \((Ω, F, P)\) with a filtration \(\{F_t, t \geq 0\}\) is called a martingale if it satisfies the following conditions:

  1. \(X_t\) is \(F_t\)-measurable for all \(t \geq 0\).

  2. \(E[|X_t|] < \infty\) for all \(t \geq 0\).

  3. \(E[X_t | F_s] = X_s,\) for all \(s < t,\) almost surely.

Analogously, a stochastic process is called a submartingale if it satisfies the first two conditions above and:

\[E[X_t | F_s] \geq X_s, \forall s < t,\]

almost surely.

Finally, a stochastic process is called a supermartingale if it satisfies the first two conditions above and:

\[E[X_t | F_s] \leq X_s, \forall s < t,\]

almost surely.

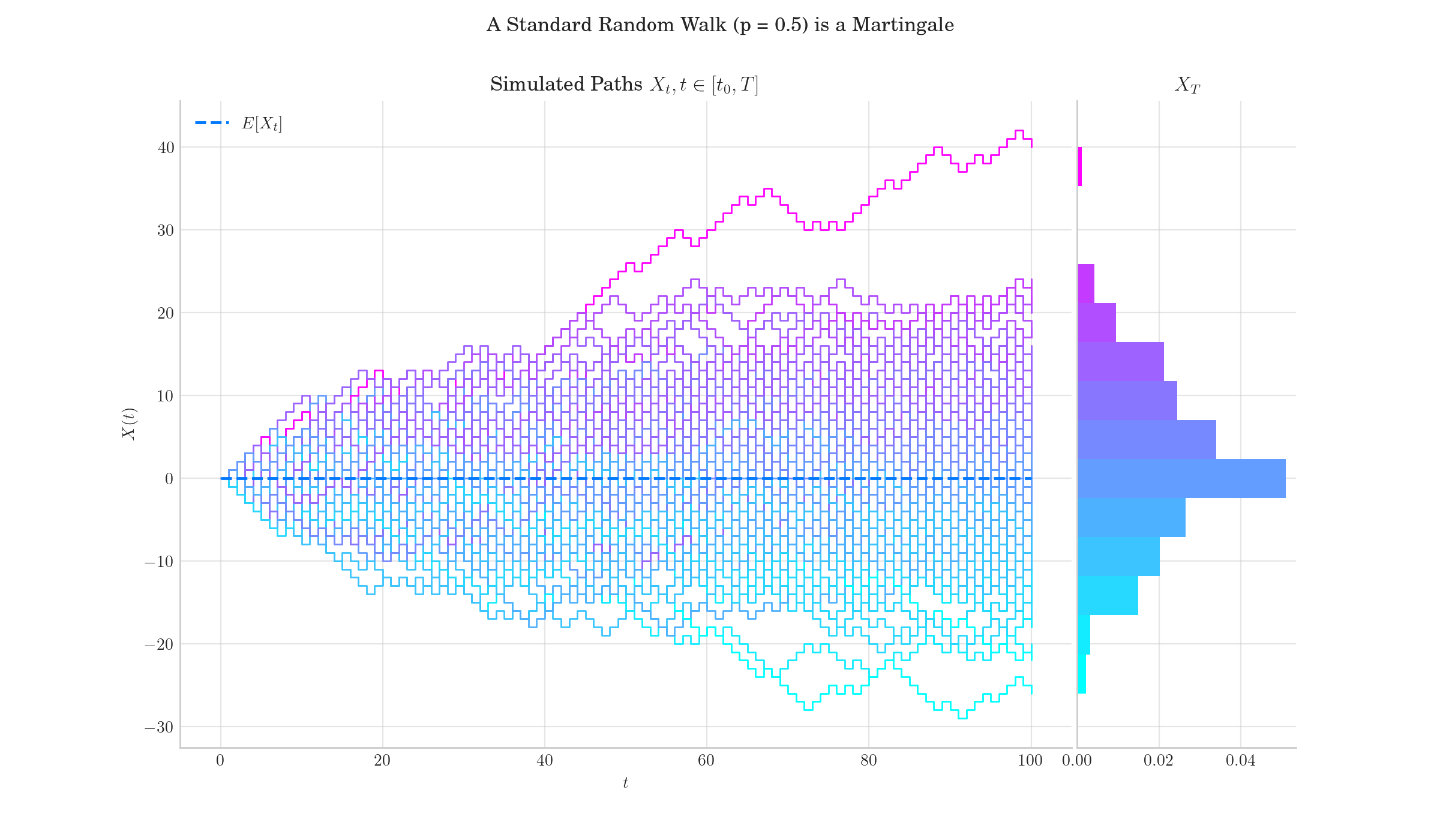
_images/sphx_glr_plot_martingale_001.png

A standard Random Walk (p = 0.5) is a Martingale.#

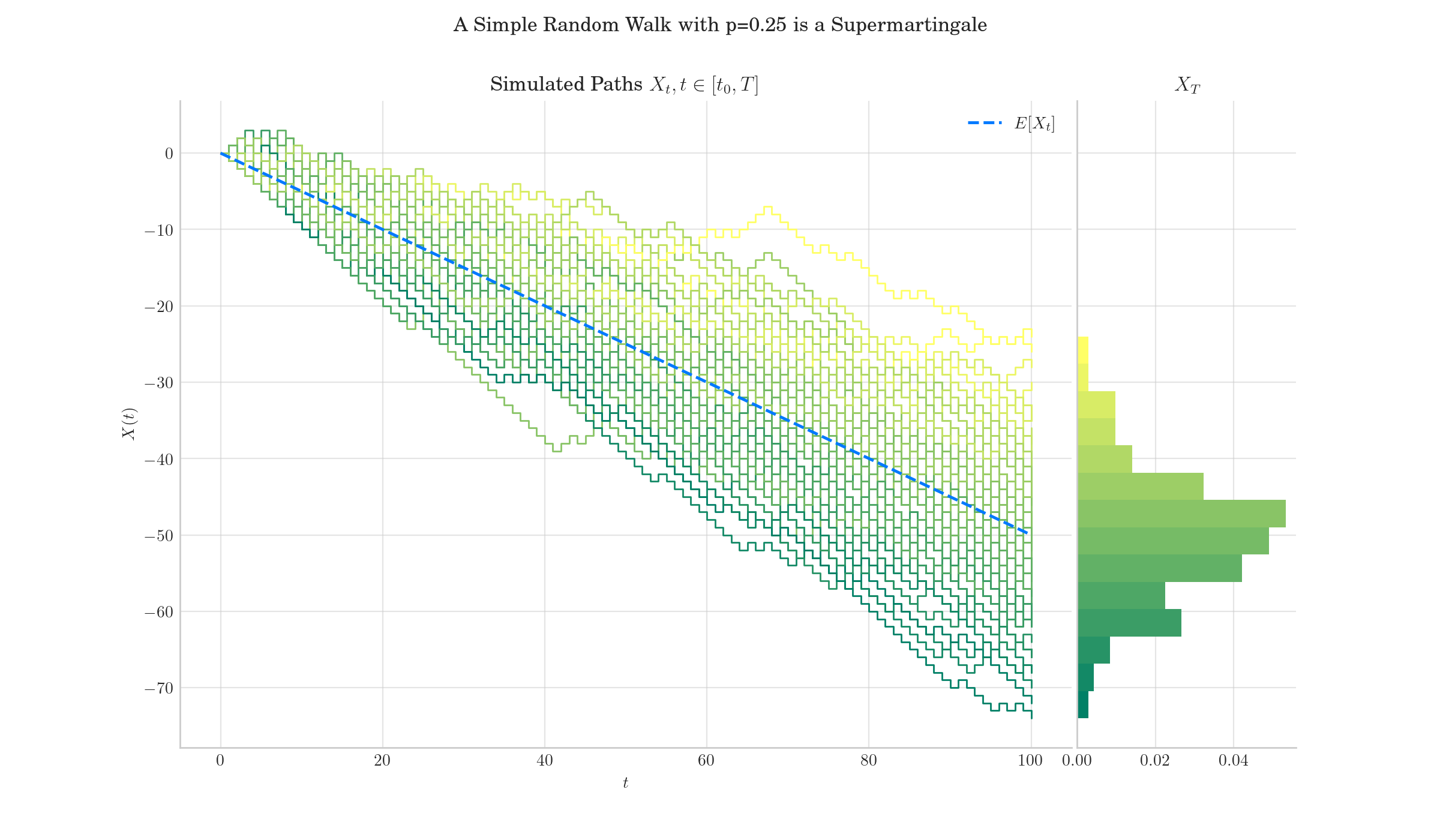
_images/sphx_glr_plot_martingale_002.png

A Biased Random Walk (p = 0.25) is not a Martingale.#

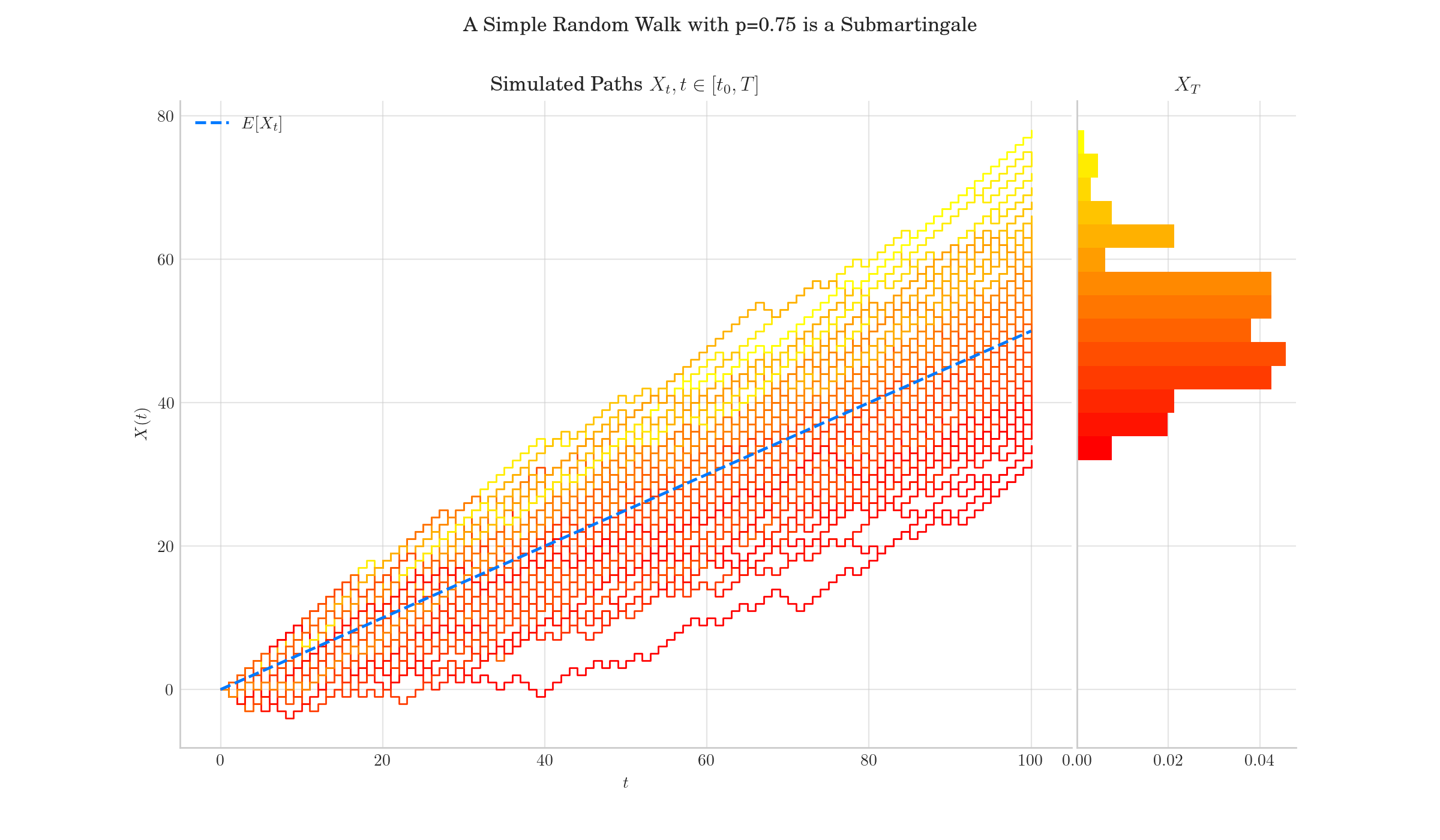
_images/sphx_glr_plot_martingale_003.png

A Biased Random Walk (p = 0.75) is not a Martingale.#

Random Facts#

  • Originally, martingale referred to a class of betting strategies that was popular in 18th-century France. The basic idea was to double the bet after each loss, so that the first win would recover all previous losses plus a profit equal to the original stake.

  • The concept of martingale in probability theory was introduced by Paul Lévy in 1934, though he did not name it. The term “martingale” was introduced later by Ville (1939), who also extended the definition to continuous martingales.

  • Martingales have applications in various fields, including finance, gambling theory, and statistical mechanics. In finance, they are used to model fair games and to price financial derivatives.

Contents