Day 16: Brownian Motion

Brownian motion, also known as Wiener process, is a continuous-time stochastic process that models random motion, often used to describe the erratic movement of particles suspended in a fluid. It is a fundamental concept in various fields such as physics, finance, and mathematics.

Definition

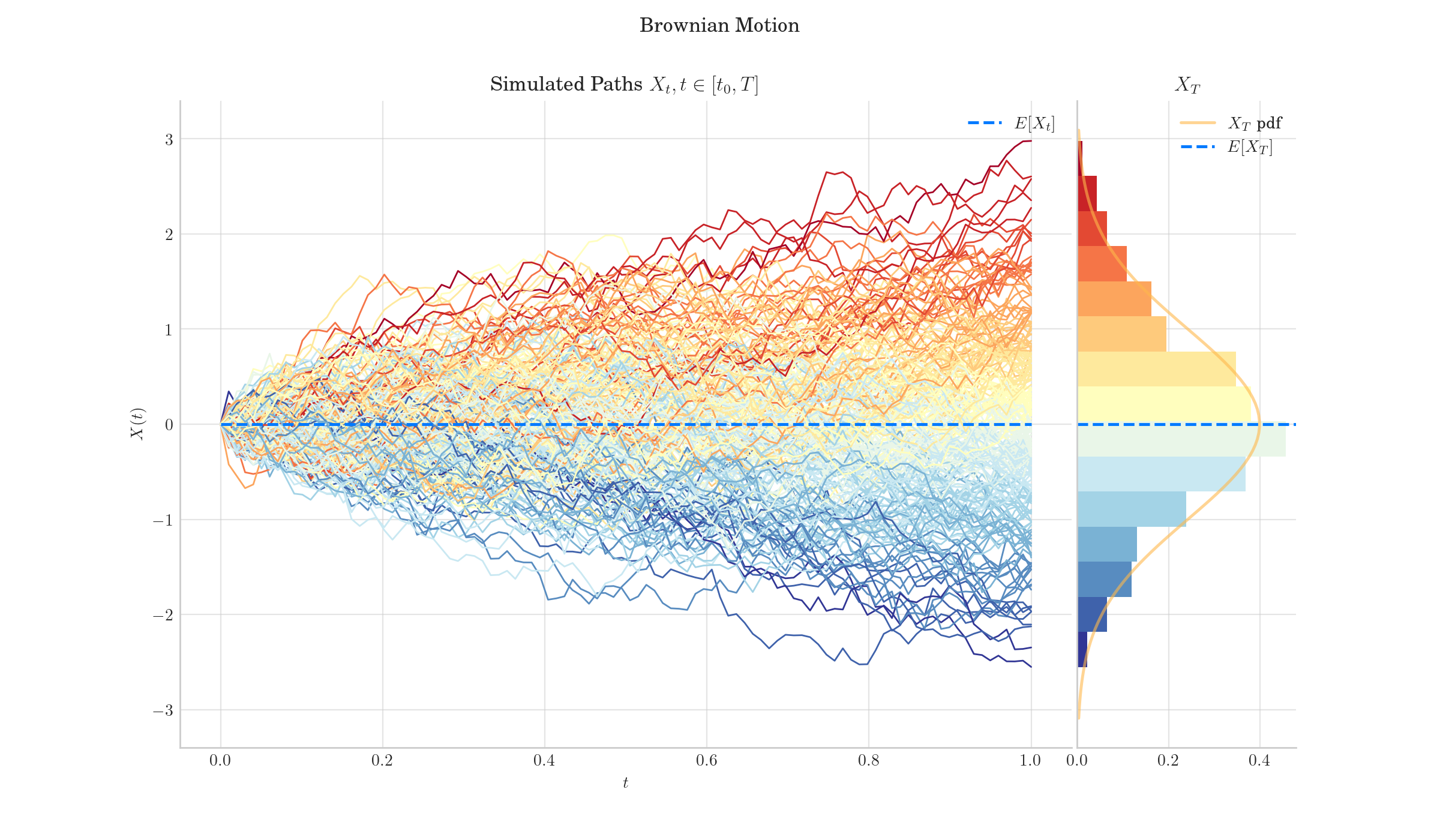
A one-dimensional standard Brownian motion \(B(t), t \geq 0\) is a stochastic process that satisfies the following properties:

1. \(B(0) = 0\) almost surely.

2. \(B(t)\) has independent increments, meaning that for any \(0 \leq s < t\), the increment \(B(t) -B(s)\) is independent of the past values \(B(u)\) for \(u \leq s\).

3. The increments are normally distributed: \(B(t) - B(s) \sim N(0, t - s)\).

4. The paths of \(B(t)\) are almost surely continuous.

Sample paths of Brownian Motion. Image made with aleatory

Random Facts

• Brownian motion is a key component in the Black-Scholes model for option pricing, where it is used to model the random behavior of asset prices over time.

• The concept of Brownian motion was first observed by the botanist Robert Brown in 1827, who noticed the random movement of pollen grains in water.

• In physics, Brownian motion provides evidence for the existence of atoms and molecules, as the random motion results from collisions with these microscopic particles.

• Brownian motion is a special case of a more general class of stochastic processes known as Lévy processes, which allow for jumps and discontinuities in their paths.

• The mathematical study of Brownian motion has led to the development of various fields such as stochastic calculus and diffusion processes, which have applications in diverse areas including biology, economics, and engineering.

• Brownian motion can be seen as the limit of a Random Walk when the step size and time intervals between steps become infinitely small. This connection is formalised in the result known as Donsker’s invariance principle or the Functional Central Limit Theorem.