Day 17: Geometric Brownian Motion

A Geometric Brownian Motion (GBM) is a continuous-time stochastic process widely used in financial mathematics to model the dynamics of asset prices. It is characterized by the property that the logarithm of the asset price follows a Brownian motion with drift. GBM is particularly popular in option pricing models, such as the Black-Scholes model, due to its ability to capture the random nature of asset price movements while ensuring that prices remain positive.

Definition

A Geometric Brownian Motion \(S(t), t \geq 0\) is defined by the stochastic differential equation (SDE):

\[dS(t) = \mu S(t) dt + \sigma S(t) dB(t)\]

where:

• \(\mu\) is the drift coefficient, representing the expected return of the asset.

• \(\sigma\) is the volatility coefficient, representing the standard deviation of the asset’s returns.

• \(B(t)\) is a standard Brownian motion (Wiener process).

The solution to this SDE can be expressed as:

\[S(t) = S(0) \exp\left(\left(\mu - \frac{1}{2} \sigma^2\right)t + \sigma B(t)\right)\]

where \(S(0)\) is the initial asset price at time \(t = 0\).

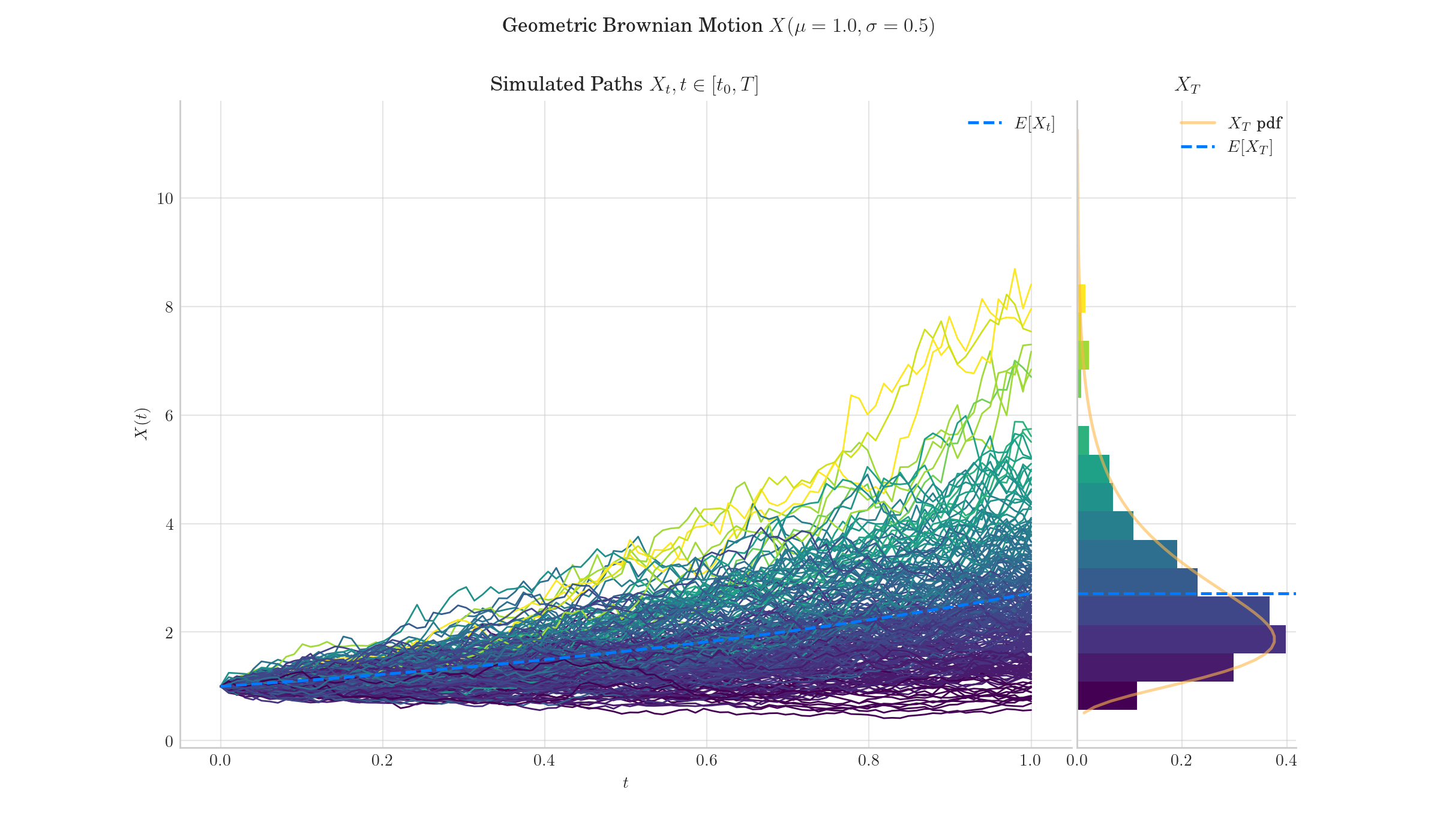
Geometric Brownian Motion Simulation. Image made with aleatory