Day 11: Normal Sampling

Contents

Day 11: Normal Sampling#

“The moral to this story is that random numbers should not be generated with a method chosen at random. Some theory should be used.”

—Donald E. Knuth, The Art of Computer Programming, Volume 2: Seminumerical Algorithms (1997)

In statistics, normal sampling refers to the process of drawing samples from a normal (Gaussian) distribution.

There are several methods to generate samples from a normal distribution. Some of the most common methods include:

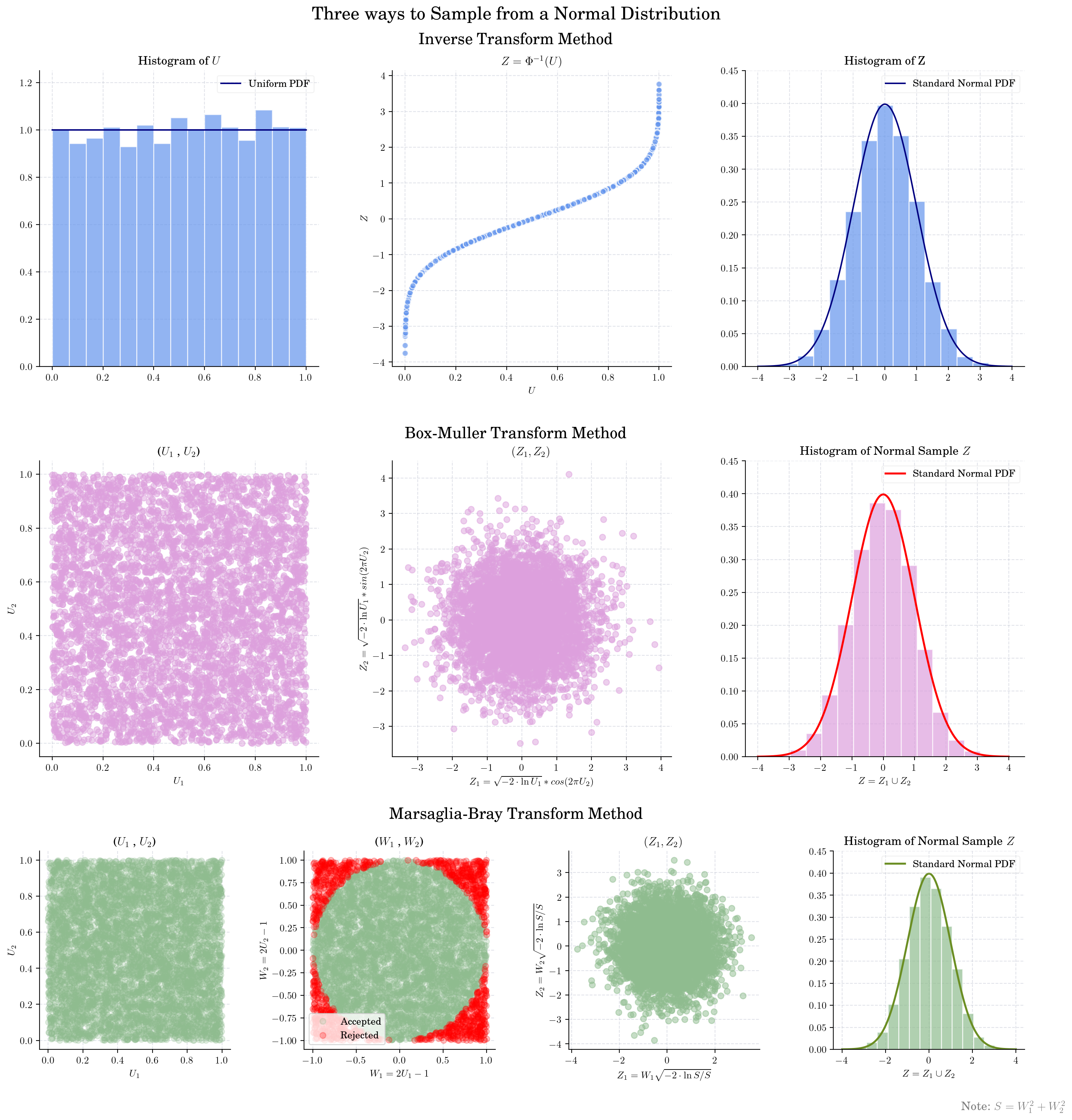
  • Inverse Transform Sampling

  • Box-Muller Transform

  • Marsaglia Polar Method

_images/normal_sampling_methods.png

Normal Sampling Methods#

  1. Inverse Transform Sampling: This method involves generating a uniform random variable and then applying the inverse of the cumulative distribution function (CDF) of the normal distribution to obtain a normally distributed random variable. However, since the CDF of the normal distribution does not have a closed-form inverse, numerical methods or approximations are typically used.

  2. Box-Muller Transform: This method generates pairs of independent standard normally distributed random variables from pairs of independent uniformly distributed random variables. The Box-Muller transform is given by the equations:

    \[ \begin{align}\begin{aligned}Z_0 = \sqrt{-2 \ln(U_1)} \cos(2\pi U_2)\\Z_1 = \sqrt{-2 \ln(U_1)} \sin(2\pi U_2)\end{aligned}\end{align} \]

    where \(U_1\) and \(U_2\) are independent random variables uniformly distributed in the interval (0, 1).

  3. Marsaglia Polar Method: This is an improvement over the Box-Muller transform that avoids the use of trigonometric functions. It generates pairs of independent standard normally distributed random variables using a rejection sampling technique. More precisely, it generates points uniformly in the unit circle and transforms them into normal variables.

    \[ \begin{align}\begin{aligned}Z_0 = V_1 \sqrt{\frac{-2 \ln(S)}{S}}\\Z_1 = V_2 \sqrt{\frac{-2 \ln(S)}{S}}\end{aligned}\end{align} \]

    where \(V_1\) and \(V_2\) are independent random variables uniformly distributed in the interval (-1, 1), and \(S = V_1^2 + V_2^2\) with the condition \(S < 1\).

Random Facts#

  • The Box-Muller transform was developed by British statistician George E. P. Box and American computer scientist Mervin E. Muller in 1958. It is widely used in computer simulations and Monte Carlo methods due to its simplicity and efficiency.

  • The Marsaglia Polar Method was developed by George Marsaglia in 1964 as an improvement over the Box-Muller transform. It is often preferred in practice due to its avoidance of trigonometric functions, which can be computationally expensive.

  • The ideas behind the Marsaglia Polar Method go back to Laplace who used similar techniques in his work on probability theory in the 18th century.

  • Many programming languages and statistical software packages provide built-in functions to generate normally distributed random variables, often using one of the methods mentioned above.

  • In Finance, normal sampling is crucial for Monte Carlo methods used in risk management, option pricing, and portfolio optimization.

Contents