Day 14 : Capital Asset Pricing Model#
“You never can predict the economy. You can’t predict the stock market. “
—Peter Lynch, One Up On Wall Street (1989)
In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio.
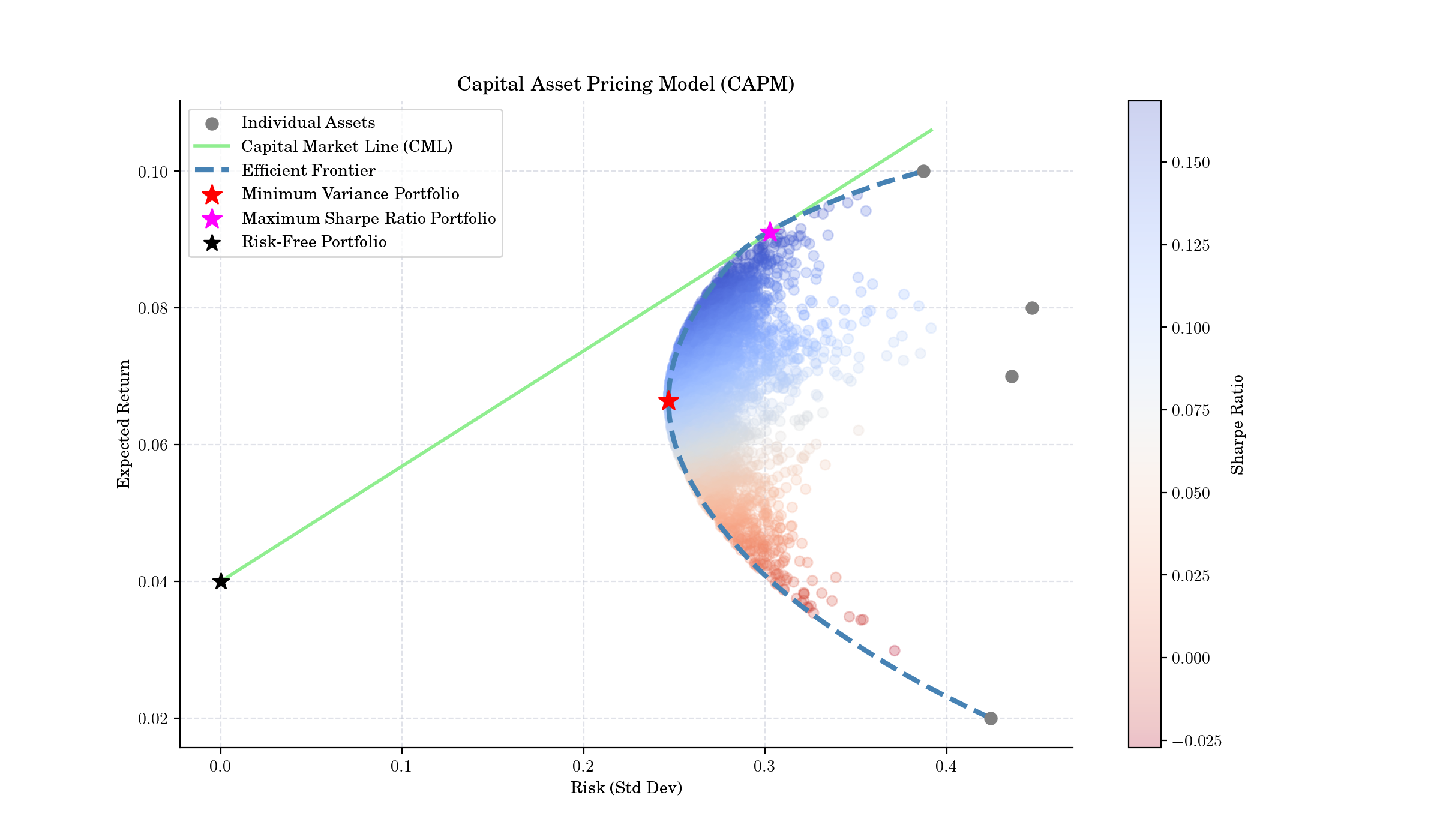
CAPM Graph showing the Capital Market Line (CML), the risk-free portfolio, market portfolio, and individual assets.#
Definition#
The CAPM is a model for pricing an individual security or portfolio. It describes the relationship between systematic risk and expected return for assets.
The model provides a required or expected rate of return for an asset using the following formula:
Where:
\(E(R_i)\) is the expected return of the asset or portfolio,
\(R_f\) is the risk-free rate of return,
\(E(R_m)\) is the expected return of the market
\(\beta_i\) (the beta) is the sensitivity of the expected excess asset returns to the expected excess market returns, also known as the systematic risk of the asset.
Moreover,
\(E(R_m) - R_f\) is known as the market risk premium
\(E(R_i) - R_f\) is known as the individual asset’s risk premium
Note 1: the expected market rate of return \(E(R_m)\) is usually estimated by measuring the arithmetic average of the historical returns on a market portfolio (e.g. S&P 500).
Note 2: the risk free rate of return \(R_f\) used for determining the risk premium is usually the arithmetic average of historical risk free rates of return and not the current risk free rate of return.
The CAPM makes several asumptions about investor behavior and market conditions:
Investor Behavior Assumptions
Aim to maximize economic utilities (Asset quantities are given and fixed).
Rational and Risk-Averse Investors: All investors are rational, risk-averse.
They only care about an investment’s expected return and risk over a single, identical time period.
Homogeneous Expectations: All investors have access to the same information and agree on the expected returns, variances, and covariances of all assets. This leads everyone to agree on the single “optimal” market portfolio.
Price Takers: No single investor’s buy or sell decisions are large enough to influence asset prices.
Market Condition Assumptions
Frictionless Markets: There are no transaction costs (brokerage fees), taxes, or restrictions on short-selling.
Perfect Marketability and Divisibility: All assets are highly liquid (marketable) and can be divided into infinitely small portions, allowing for any portfolio combination.
Unlimited Borrowing and Lending: Investors can borrow or lend an unlimited amount of capital at a single, constant risk-free rate of return.
Efficient Markets: All available information is quickly and universally distributed and absorbed, meaning asset prices fully reflect all known information at all times.
Market Portfolio Includes All Assets: The true “market portfolio” includes all existing risky assets globally, weighted by their market value.
Interpretation#
The CAPM suggests that the expected return of an asset is determined by its sensitivity to market risk (beta), the risk-free rate, and the expected market return. A higher beta indicates higher risk and thus a higher expected return.
The beta is calculated as follows:
where: - \(Cov(R_i, R_m)\) is the covariance between the asset’s returns and the market’s returns - \(Var(R_m)\) is the variance of the market’s returns
