Day 19: Discretisation Schemes

There are two primary discretisation schemes used in numerical simulations of stochastic processes: the Euler-Maruyama method and the Milstein method. These methods are essential for approximating solutions to stochastic differential equations (SDEs) that cannot be solved analytically.

Euler-Maruyama

This method is a straightforward extension of the Euler method for ordinary differential equations to stochastic differential equations. It is widely used due to its simplicity and ease of implementation.

Given an SDE of the form:

\[dX_t = a(X_t, t) dt + b(X_t, t) dW_t\]

where \(a(X_t, t)\) is the drift coefficient, \(b(X_t, t)\) is the diffusion coefficient, and \(W_t\) is a Wiener process (Brownian motion), the Euler-Maruyama discretisation is given by:

\[X_{t+\Delta t} = X_t + a(X_t, t) \Delta t + b(X_t, t) \Delta W_t\]

where \(\Delta W_t\) is a normally distributed random variable with mean 0 and variance \(\Delta t\).

Milstein

The Milstein method is a higher-order discretisation scheme that provides better accuracy than the Euler-Maruyama method, especially for SDEs with non-linear diffusion terms. It includes an additional term that accounts for the derivative of the diffusion coefficient.

The Milstein discretisation is given by:

\[X_{t+\Delta t} = X_t + a(X_t, t) \Delta t + b(X_t, t) \Delta W_t + \frac{1}{2} b(X_t, t) b'(X_t, t) \left( (\Delta W_t)^2 - \Delta t \right)\]

where \(b'(X_t, t)\) is the derivative of the diffusion coefficient with respect to \(X_t\).

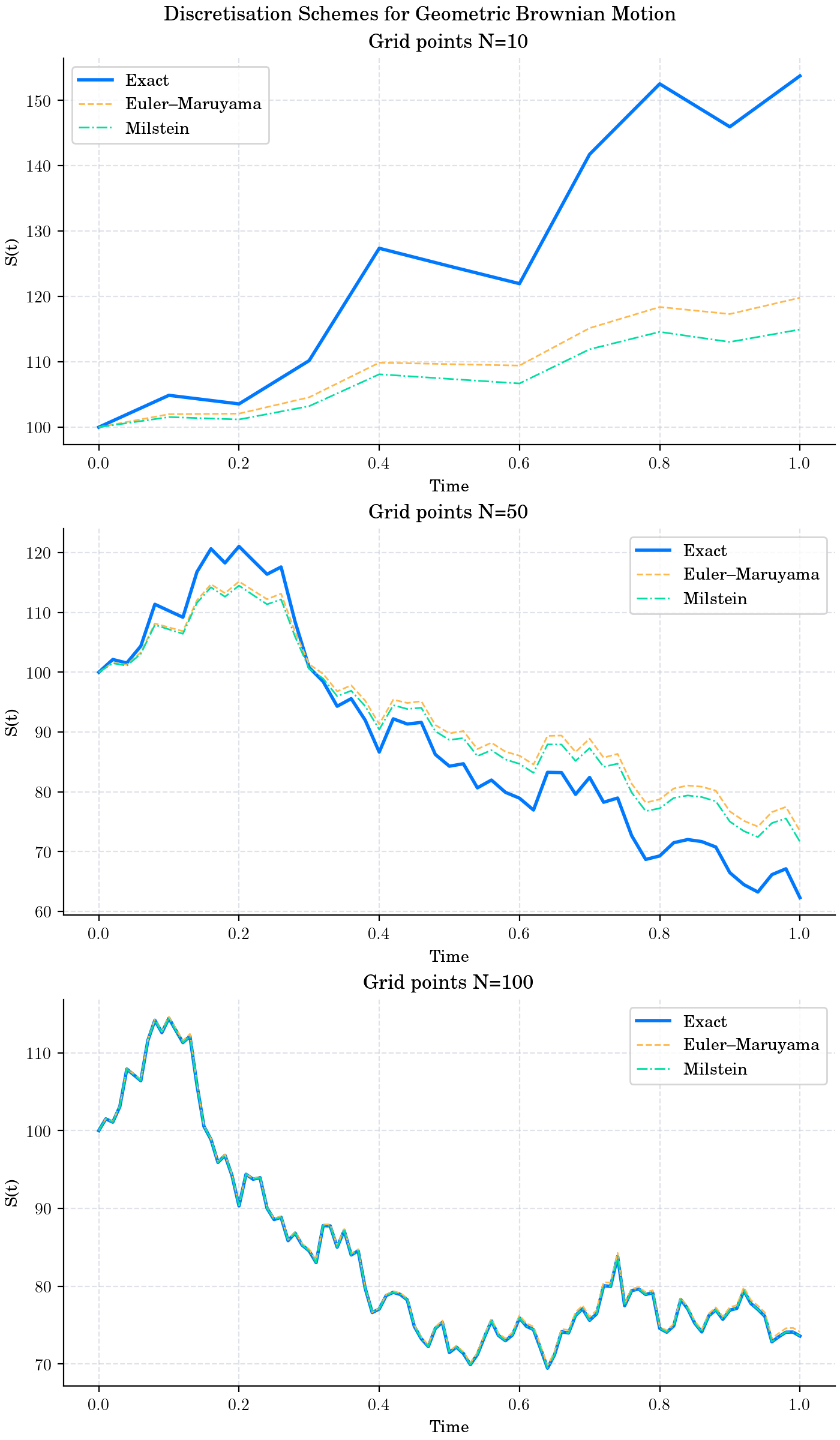
Comparison of Euler-Maruyama and Milstein Discretisation Schemes.