Day 15: Random Walk

Day 15: Random Walk#

“What begins as a random walk often ends up taking you somewhere, somewhere that you later realise was exactly where you wanted to go” ― David Byrne

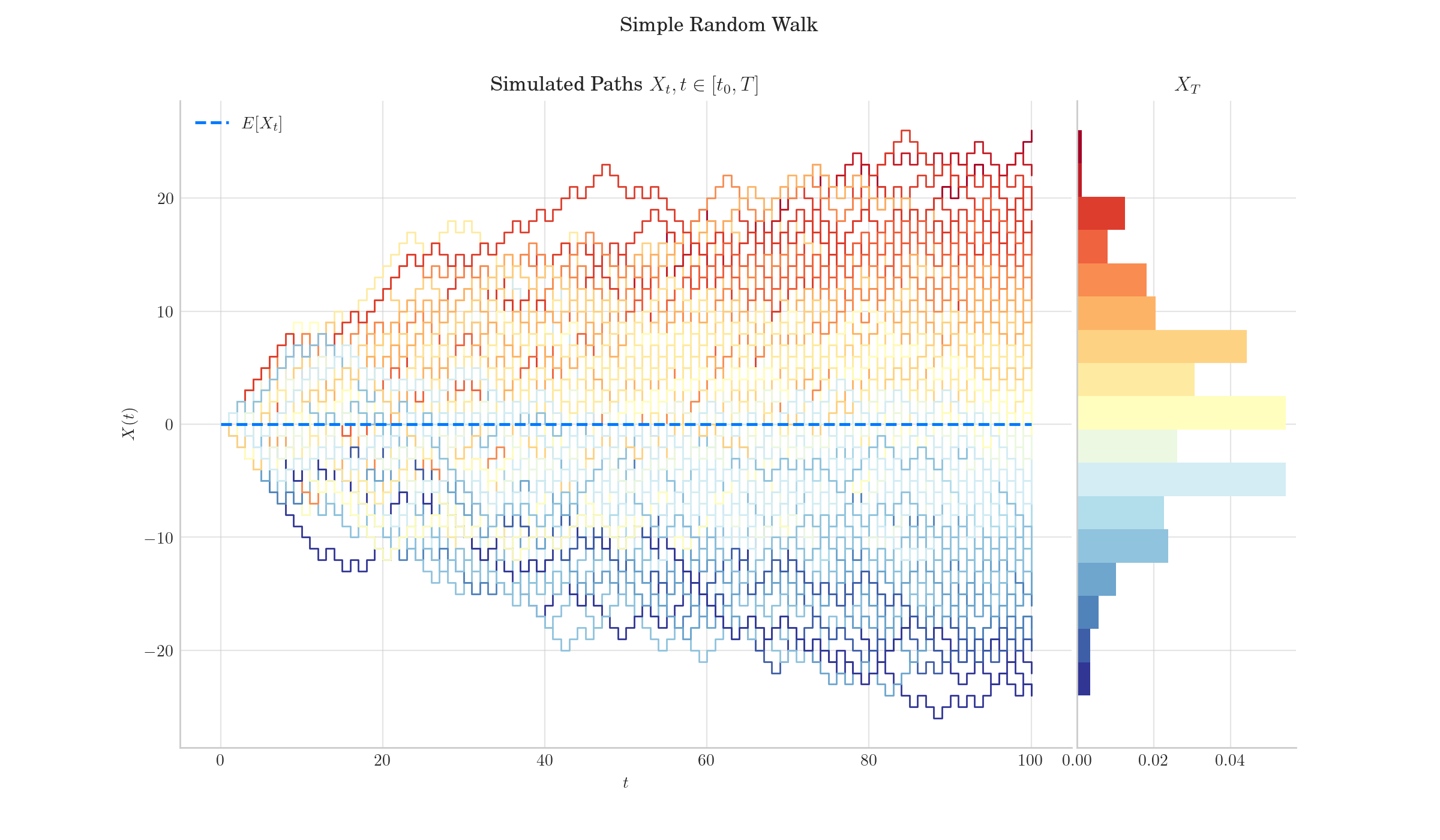
A random walk is a mathematical object, often used to model seemingly random processes in various fields such as physics, economics, and finance. It describes a path consisting of a succession of random steps. In its simplest form, a random walk can be visualized as a particle moving in one-dimensional space, where at each time step, it moves either one unit to the left or one unit to the right with equal probability.

In financial mathematics, random walks are frequently used to model stock prices and market indices, based on the idea that price changes are random and unpredictable.

Definition#

Let \(Z_i, i = 1, 2, ...\) be a sequence of real-valued independent an identically distributed (i.i.d.) random variables defined on a probability space \((Ω, F, P)\). The random walk \(S_n\) is defined as:

\[S_n = \sum_{i=1}^{n} Z_i, \quad n \geq 1, \quad S_0 = 0\]

where \(S_n\) represents the position of the random walk after \(n\) steps.

Random Walk Simulation

Simple Random Walk. Image made with aleatory#

Random Facts#

  • The term random walk was introduced by English biostatistician and mathematician Karl Pearson in a letter to the journal Nature in 1905. In this letter, Pearson described a problem that involved a person taking a series of steps in random directions and inquired about the resulting distance from the starting point after a large number of steps:

  • A Random Walk in one or two dimensions is recurrent, meaning that a walker starting at a point will, with probability 1, eventually return to that point. However, in three or more dimensions, the Random Walk becomes transient, where there is a non-zero probability that the walker will never return to the starting point. This fascinating result is known as Pólya’s Recurrence Theorem.

  • The expected distance from the origin after :math: n steps in a simple random walk is proportional to :math: sqrt{n}, indicating that the walk spreads out over time.

  • Random walks have applications in various fields, including physics (e.g., modeling particle diffusion), biology (e.g., animal foraging behavior), and computer science (e.g., algorithms for network routing and search).

  • In epidemiology, Random Walks can model the spread of infectious diseases by simulating how individuals move and interact in a population. This helps in predicting infection patterns and formulating strategies to mitigate outbreaks.

Contents