Day 4 : Probability Distributions#
“The theory of probabilities is basically only common sense reduced to a calculus. It makes one estimate accurately what right-minded people feel by a sort of instinct, often without being able to give a reason for it”
—Pierre-Simon Laplace (1825)
In probability theory and statistics, a probability distribution is a function that gives the probabilities of occurrence of possible events for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space).
There are lots of different probability distributions, each with its own characteristics and applications. But today we will focus on some of the most important probability distributions in mathematical finance and statistics ⭐️.
Normal Distribution#
Also known as the Gaussian distribution after German mathematician Carl Friedrich Gauss, is probably the most popular probability distribution. It has became ubiquitous in many areas of knowledge and most people recognise its familiar bell-shaped curve. It has support in \((-\infty, \infty)\) and is defined by two parameters. The shape parameter \(\mu\) is the mean or expectation of the distribution (and also its median and mode!), while the scale parameter \(\sigma\) is its standard deviation.
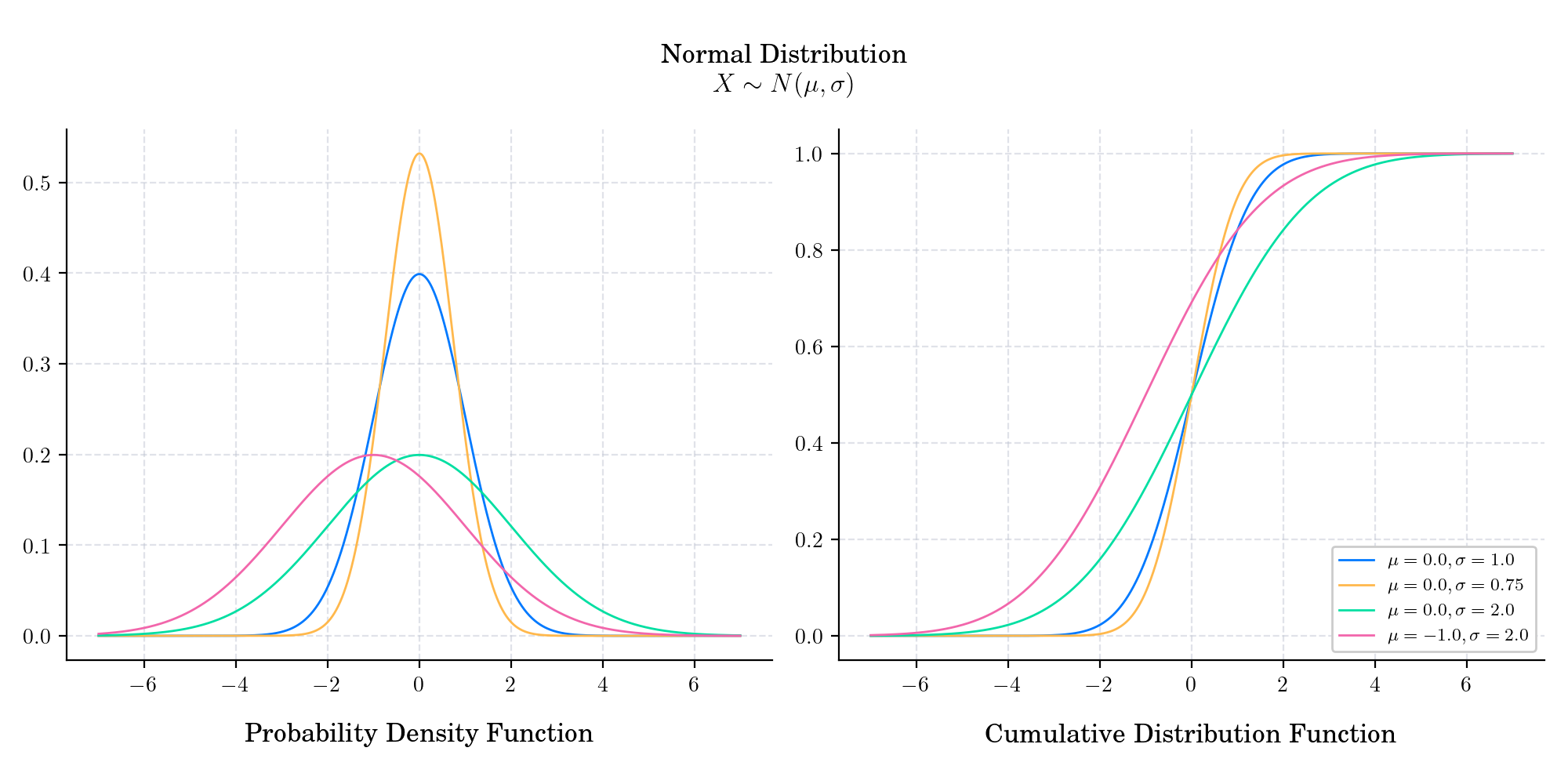
In finance, the normal distribution appears as the marginal distribution of many diffusion models such as the Ornstein-Uhlenbeck process used to model interest rates, currency exchange rates, and commodity prices.
LogNormal#
A lognormal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable X is log-normally distributed, then Y = ln(X) has a normal distribution. Equivalently, if Y has a normal distribution, then the exponential function of Y, X = exp(Y) , has a log-normal distribution.
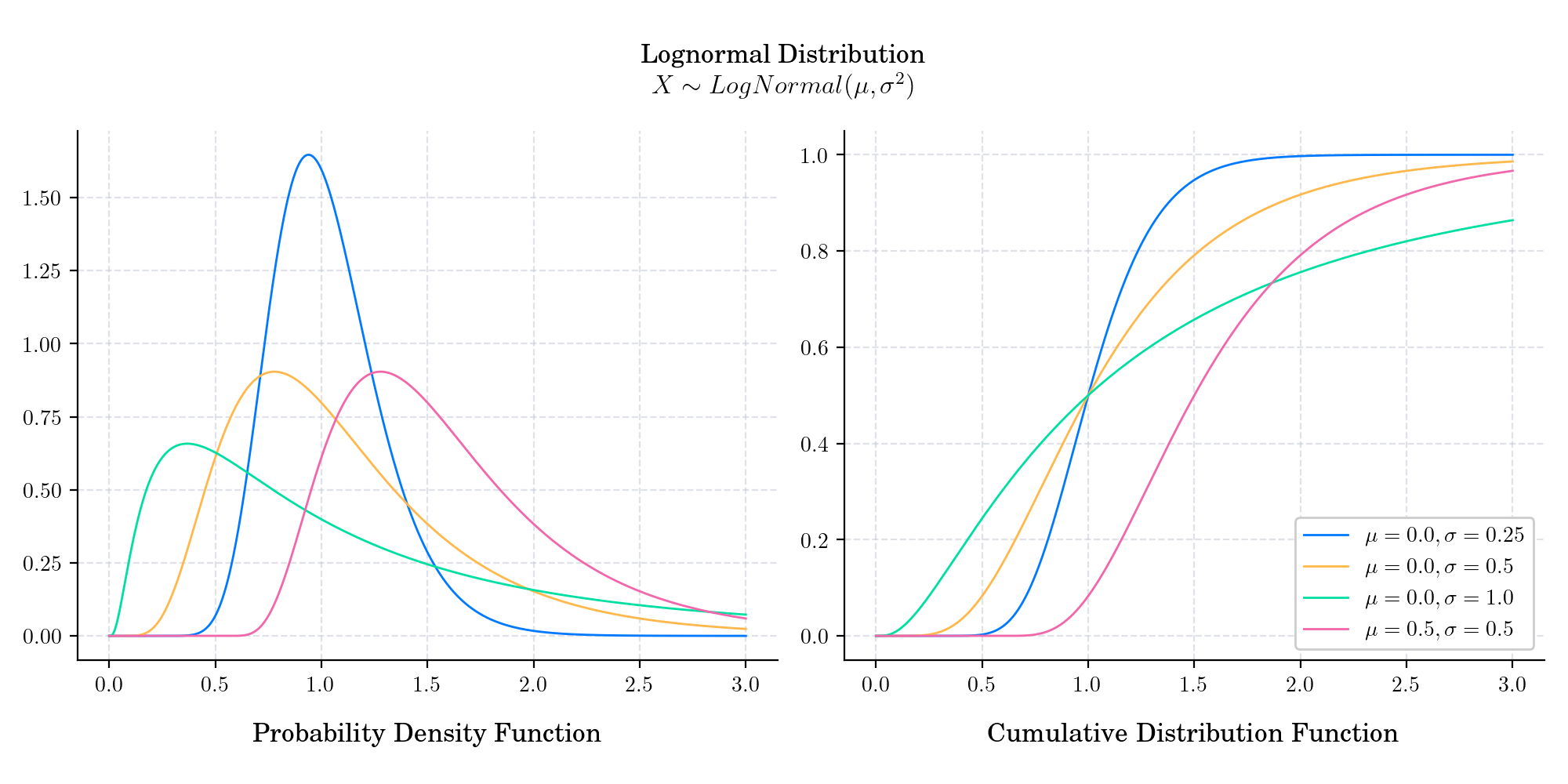
It is extensively used in Finance. In particular, the famous Black and Scholes models relies on the assumption that the stock price follows a geometric Brownian motion. This means that the marginal densities of the stock price follow a log-normal distribution.
It is often used to model stock prices and other financial variables that cannot be negative.
Chi Distribution#
The chi distribution is a continuous probability distribution with support in \([0, \infty)\). It is the distribution of the positive square root of a sum of squared independent standard normal random variables. Equivalently, it is the distribution of the Euclidean distance between a multivariate Gaussian random variable and the origin.
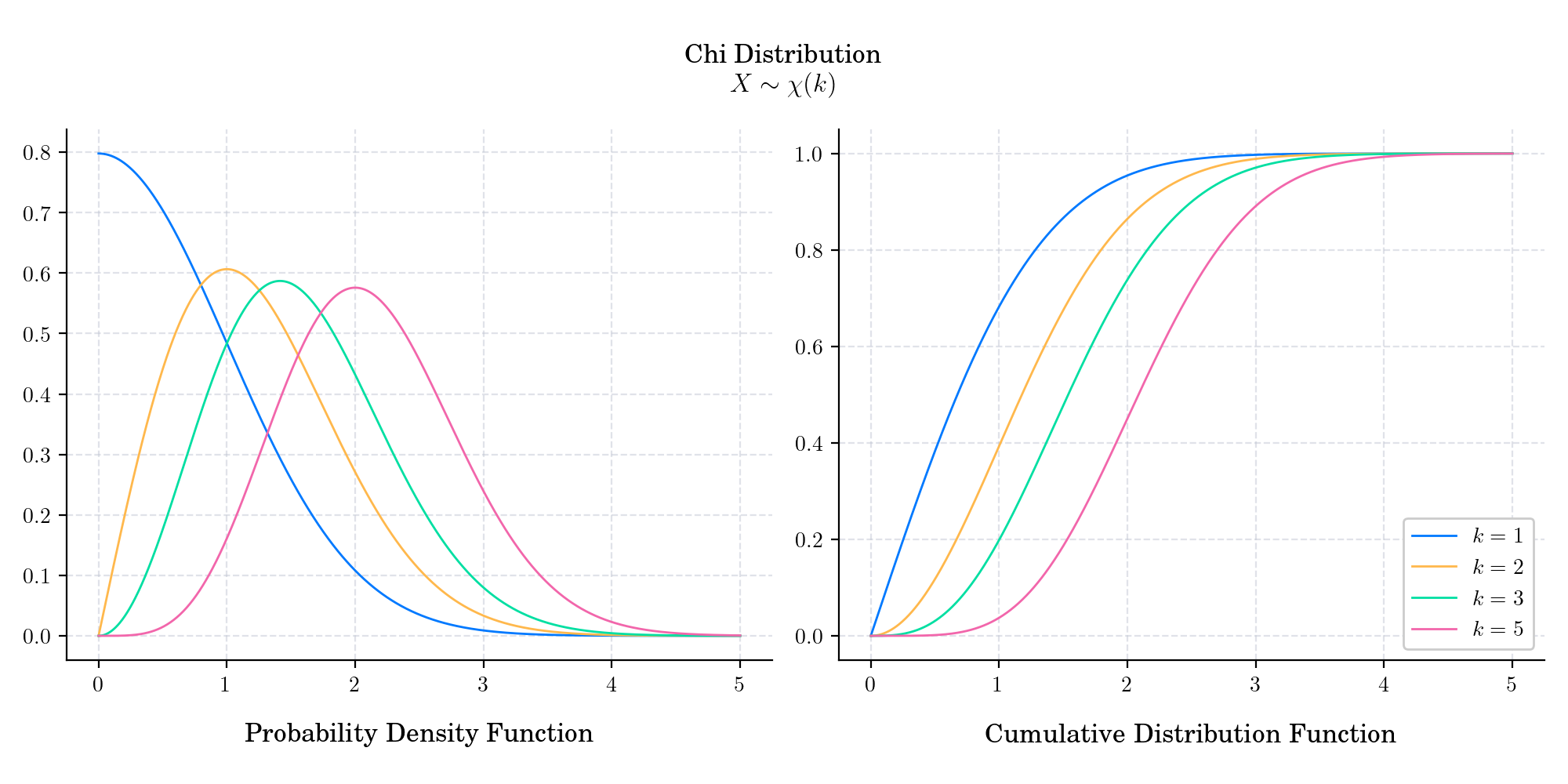
In finance, the chi distribution is used in various applications, including risk management and portfolio optimization. It also arise as the marginal distribution of the Bessel processes used to model interest rates and volatility.
Student’s t-Distribution#
The Student’s t-distribution (or simply the t-distribution) is a continuous probability distribution that generalises the standard normal distribution. Like the latter, it has support \((-\infty, \infty)\), is symmetric around zero, and bell-shaped. However, it has heavier tails and the amount of probability mass in the tails is controlled by its parameter \(\nu>0\), which is known as degrees of freedom.
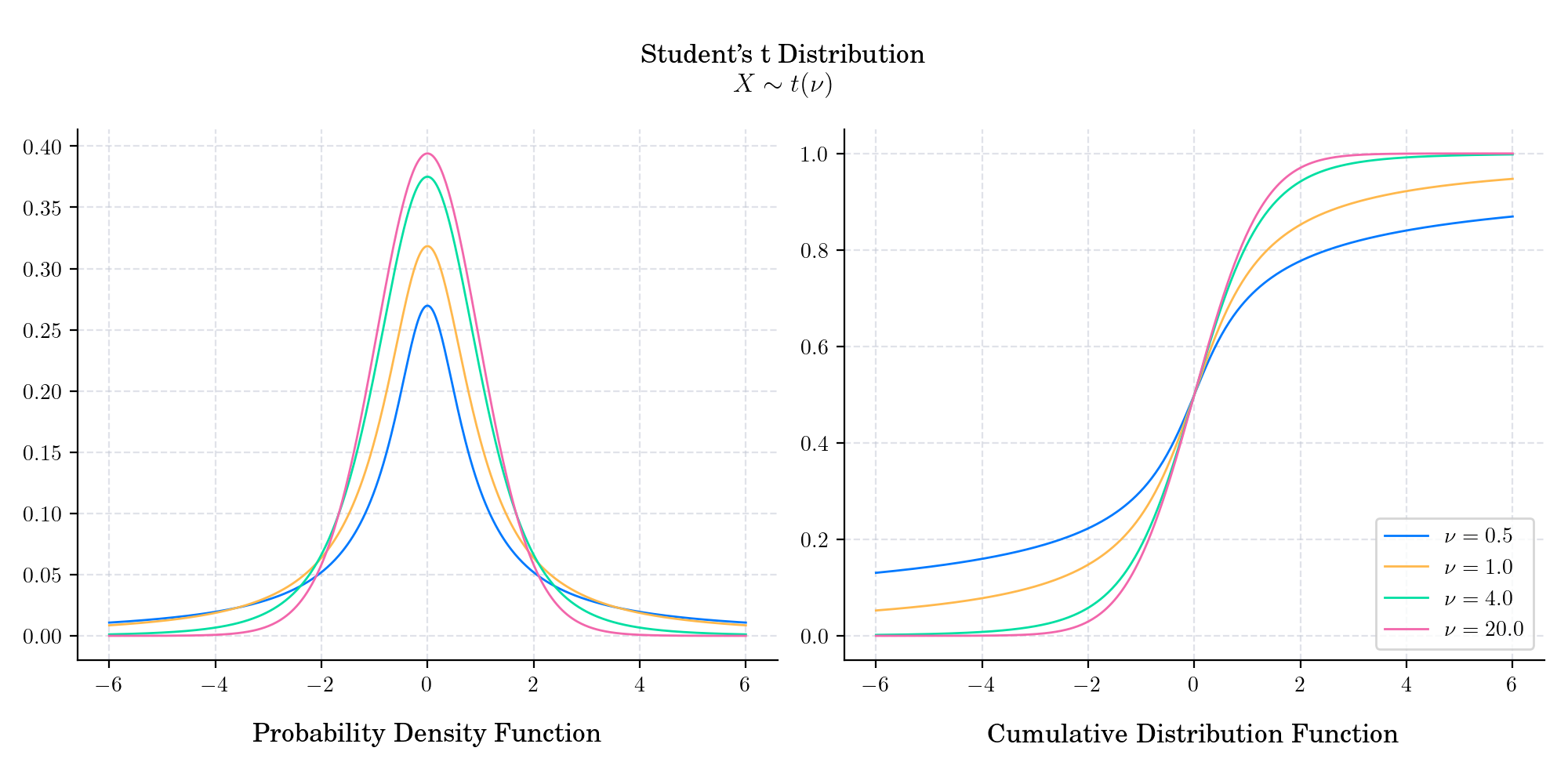
In finance, the t-distribution is often used to model asset returns that exhibit fat tails and excess kurtosis compared to the normal distribution.
Exponential Distribution#
The exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It has support \([0, \infty)\) and is defined by a parameter \(\lambda>0\) which is called rate (or inverse scale).
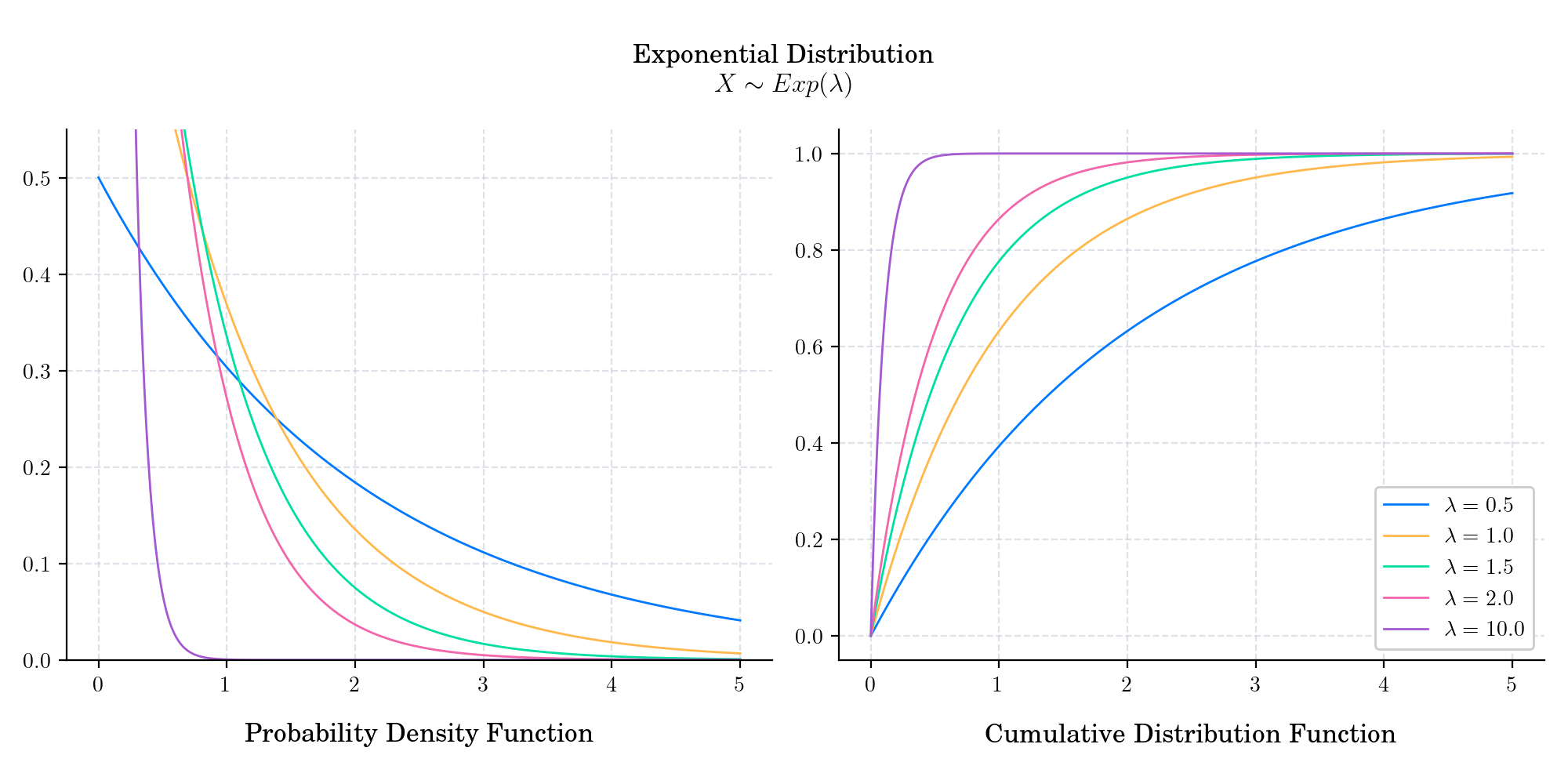
In finance, the exponential distribution is often used to model the time until default of a credit instrument or the time between trades in a financial market.
Note
If you are interested in learning more about probablity distributions, please visit the previous Advent Calendar on Probability Distributions here
