Day 20: Orstein-Uhlenbeck Process

Day 20: Orstein-Uhlenbeck Process#

The Ornstein-Uhlenbeck (OU) process is a stochastic process that plays a critical role in fields like physics, finance, and biology. It is a type of Gaussian process known for its mean-reverting properties, making it particularly useful for modelling phenomena that oscillate around a long-term average.

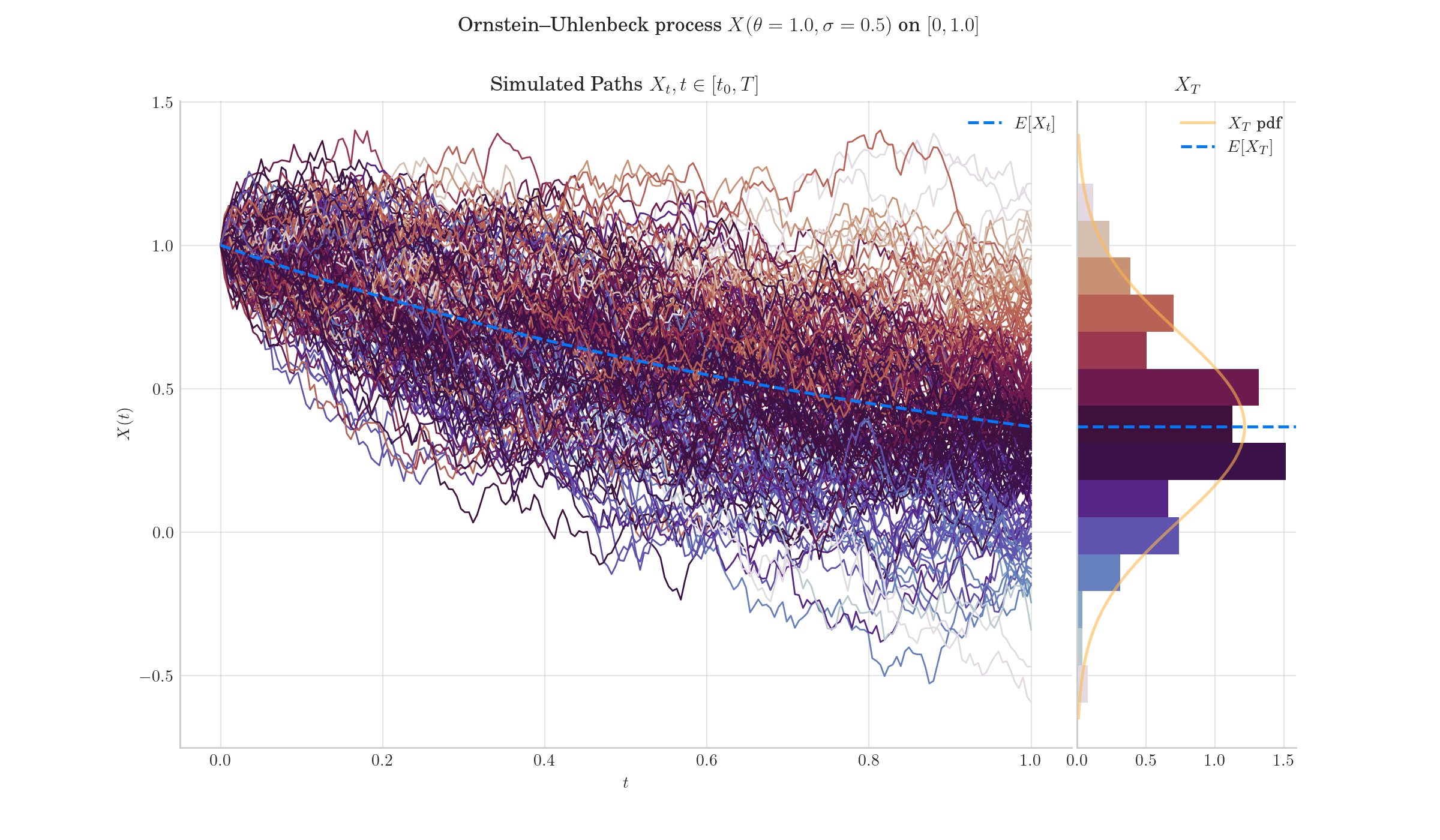
OU Process Simulation

Simulation of an Orstein-Uhlenbeck Process. Image made with aleatory#

Definition#

The OU process is defined by the following stochastic differential equation (SDE):

\[dX_t = \theta (\mu - X_t) dt + \sigma dW_t\]

where:

  • \(X_t\) is the value of the process at time :math:`t

  • \(\theta > 0\) is the rate of mean reversion

  • \(\mu\) is the long-term mean level

  • \(\sigma > 0\) is the volatility parameter

  • \(W_t\) is a standard Wiener process (Brownian motion)

OU Process Simulation

Random Facts#

  • The process was introduced by physicists Leonard Ornstein and George Eugene Uhlenbeck in 1930 to describe the velocity of a massive particle undergoing Brownian motion in a viscous fluid.

  • The Ornstein–Uhlenbeck process can also be considered as the continuous-time analogue of the discrete-time AR(1) process.

  • The Ornstein–Uhlenbeck process is a stationary Gauss–Markov process, which means that it is a Gaussian process, a Markov process, and is temporally homogeneous. In fact, it is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables.

Contents