Day 12: Sharpe Ratio

Contents

Day 12: Sharpe Ratio#

“Some investments do have higher expected returns than others. Which ones? Well, by and large they’re the ones that will do the worst in bad times.”

—William F. Sharpe

The Sharpe Ratio, developed by Nobel laureate William F. Sharpe in 1966, is a widely used metric in finance to assess the risk-adjusted return of an investment or portfolio. It measures the excess return (or risk premium) per unit of risk taken, allowing investors to compare the performance of different investments on a level playing field. The Sharpe Ratio is calculated using the following formula:

\[S = \frac{ \mathbb{E} [ R_p - R_f]}{\sigma_p}\]

where

  • \(R_p\) is the return of the portfolio,

  • \(R_f\) is the risk-free rate of return, e.g. the return on government bonds

  • \(\sigma_p\) is the standard deviation of the portfolio’s excess returns (a measure of risk).

A higher Sharpe Ratio indicates a more favorable risk-adjusted return, meaning that the investment provides a higher return for each unit of risk taken.

The Sharpe Ratio is particularly useful for comparing portfolios or investments with different levels of risk. For example, consider two portfolios: Portfolio A has an expected return of 8% with a standard deviation of 10%, while Portfolio B has an expected return of 10% with a standard deviation of 20%. Assuming a constant risk-free rate of 2%, we can calculate the Sharpe Ratios for both portfolios:

  • Portfolio A: \(S_A = \frac{0.08 - 0.02}{0.10} = 0.60\)

  • Portfolio B: \(S_B = \frac{0.10 - 0.02}{0.20} = 0.40\)

In this example, Portfolio A has a higher Sharpe Ratio (0.60) compared to Portfolio B (0.40), indicating that Portfolio A provides a better risk-adjusted return despite having a lower expected return.

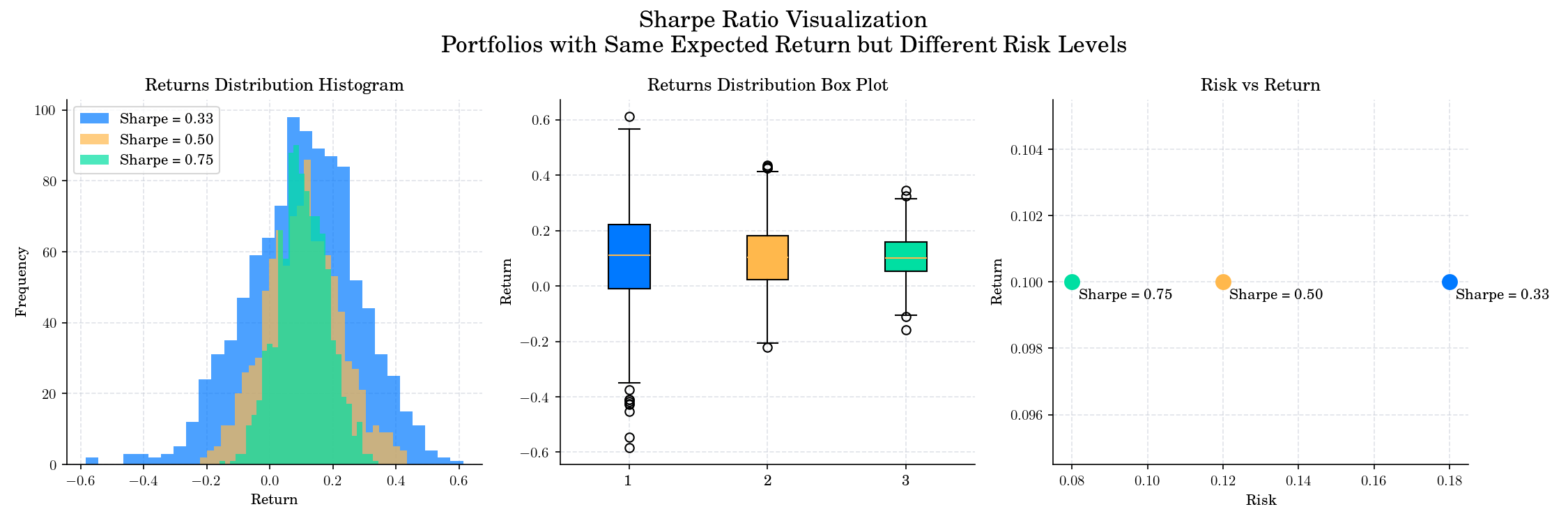
_images/sphx_glr_plot_sharpe_ratio_001.png

Sharpe Ratio Comparison of Three Portfolios with the same expected return but different risk levels.#

Random Facts#

  • William F. Sharpe was awarded the Nobel Prize in Economic Sciences in 1990 for his contributions to the theory of financial economics, particularly for the development of the Capital Asset Pricing Model (CAPM) and the Sharpe Ratio.

  • The Sharpe Ratio is widely used by portfolio managers and investors to evaluate the performance of mutual funds, hedge funds, and other investment vehicles.

  • While the Sharpe Ratio is a valuable tool for assessing risk-adjusted returns, it has limitations, such as assuming that returns are normally distributed and not accounting for higher moments of the return distribution (e.g., skewness and kurtosis).

Contents